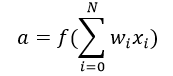从零学习：从Python和R理解和编码神经网络（完整版）

作者： SUNIL RAY

编译：Bot

编者按：当你面对一个新概念时，你会怎么学习和实践它？是耗费大量时间学习整个理论，掌握背后的算法、数学、假设、局限再亲身实践，还是从最简单的基础开始，通过具体项目解决一个个难题来提高你对它的整体把握？在这系列文章中，论智将采用第二种方法和读者一起从头理解机器学习。

“从零学习”系列第一篇从Python和R理解和编码神经网络来自Analytics Vidhya博主、印度资深数据科学开发人员SUNIL RAY。

本文将围绕神经网络构建的基础知识展开，并集中讨论网络的应用方式，用Python和R语言实战编码。

目录

• 神经网络的基本工作原理

• 多层感知器及其基础知识

• 神经网络具体步骤详解

• 神经网络工作过程的可视化

• 如何用Numpy实现NN（Python）

• 如何用R语言实现NN

• 反向传播算法的数学原理

神经网络的基本工作原理

如果你是一名开发者，或曾参与过编程项目，你一定知道如何在代码中找bug。通过改变输入和环境，你可以用相应的各种输出测试bug位置，因为输出的改变其实是一个提示，它能告诉你应该去检查哪个模块，甚至是哪一行。一旦你找到正确的那个它，并反复调试，你总会得到理想的结果。

神经网络其实也一样。它通常需要几个输入，在经过多个隐藏层中神经元的处理后，它会在输出层返回结果，这个过程就是神经网络的“前向传播”。

得到输出后，接下来我们要做的就是用神经网络的输出和实际结果做对比。由于每一个神经元都可能增加最终输出的误差，所以我们要尽可能减少这个损耗（loss），使输出更接近实际值。那该怎么减少loss呢？

在神经网络中，一种常用的做法是降低那些容易导致更多loss的神经元的权重/权值。因为这个过程需要返回神经元并找出错误所在，所以它也被称为“反向传播”。

为了在减少误差的同时进行更少量的迭代，神经网络也会使用一种名为“梯度下降”（Gradient Descent）的算法。这是一种基础的优化算法，能帮助开发者快速高效地完成各种任务。

虽然这样的表述太过简单粗浅，但其实这就是神经网络的基本工作原理。简单的理解有助于你用简单的方式去做一些基础实现。

多层感知器及其基础知识

就像原子理论中物质是由一个个离散单元原子所构成的那样，神经网络的最基本单位是感知器（Perceptron）。那么，感知器是什么？

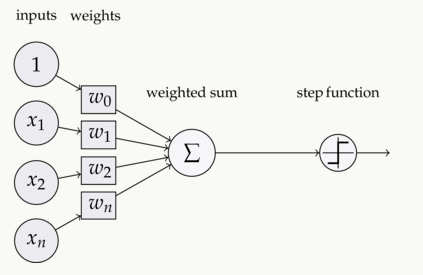
对于这个问题，我们可以这么理解：感知器就是一种接收多个输入并产生一个输出的东西。如下图所示：

感知器

示例中的它有3个输入，却只有一个输出，由此我们产生的下一个合乎逻辑的问题就是输入和输出之间的对应关系是什么。让我们先从一些基本方法入手，再慢慢上升到更复杂的方法。

以下是我列举的3种创建输入输出对应关系的方法：

1. 直接组合输入并根据阈值计算输出。例如，我们设x1=0，x2=1，x3=1，阈值为0。如果x1+x2+x3>0，则输出1；反之，输出0。可以看到，在这个情景下上图的最终输出是1。

2. 接下来，让我们为各输入添加权值。例如，我们设x1、x2、x3三个输入的权重分别为w1、w2、w3，其中w1=2，w2=3，w3=4。为了计算输出，我们需要将输入乘以它们各自的权值，即2x1+3x2+4x3，再和阈值比较。可以发现，x3对输出的影响比x1、x2更大。

3. 接下来，让我们添加bias（偏置，有时也称阈值，但和上文阈值有区别）。每个感知器都有一个bias，它其实也是一种加权方式，可以反映感知器的灵活性。bias在某种程度上相当于线性方程y=ax+b中的常数b，可以让函数上下移动。如果b=0，那分类线就要经过原点（0，0），这样神经网络的fit范围会非常受限。例如，如果一个感知器有两个输入，它就需要3个权值，两个对应给输入，一个给bias。在这个情景下，上图输入的线性形式就是w1x1 + w2x2 + w3x3+1×b。

但是，这样做之后每一层的输出还是上层输入的线性变换，这就有点无聊。于是人们想到把感知器发展成一种现在称之为神经元的东西，它能将非线性变换（激活函数）用于输入和loss。

什么是激活函数（activation function）？

激活函数是把加权输入（w1x1 + w2x2 + w3x3+1×b）的和作为自变量，然后让神经元得出输出值。

在上式中，我们将bias权值1表示为x0，将b表示为w0.

输入—加权—求和—作为实参被激活函数计算—输出

它主要用于进行非线性变换，使我们能拟合非线性假设、估计复杂函数，常用的函数有：Sigmoid、Tanh和ReLu。

前向传播、反向传播和Epoch

到目前为止，我们已经由输入计算获得了输出，这个过程就是“前向传播”（Forward Propagation）。但是，如果产出的估计值和实际值误差太大怎么办？其实，神经网络的工作过程可以被看作是一个试错的过程，我们能根据输出值的错误更新之前的bias和权值，这个回溯的行为就是“反向传播”（Back Propagation）。

反向传播算法（BP算法）是一种通过权衡输出层的loss或错误，将其传回网络来发生作用的算法。它的目的是重新调整各项权重来使每个神经元产生的loss最小化，而要实现这一点，我们要做的第一步就是基于最终输出计算每个节点之的梯度（导数）。具体的数学过程我们会在最后一节“反向传播算法的数学原理”中详细探讨。

而这个由前向传播和反向传播构成的一轮迭代就是我们常说的一个训练迭代，也就是Epoch。

多层感知器

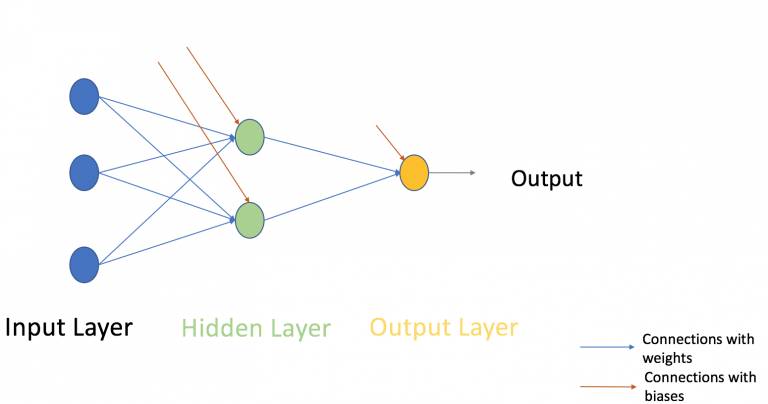
现在，让我们继续回到例子，把注意力放到多层感知器上。截至目前，我们看到的只有一个由3个输入节点x1、x2、x3构成的单一输入层，以及一个只包含单个神经元的输出层。诚然，如果是解决线性问题，单层网络确实能做到这一步，但如果要学习非线性函数，那我们就需要一个多层感知器（MLP），即在输入层和输出层之间插入一个隐藏层。如下图所示：

图片中的绿色部分表示隐藏层，虽然上图只有一个，但事实上，这样一个网络可以包含多个隐藏层。同时，需要注意的一点是，MLP至少由三层节点组成，并且所有层都是完全连接的，即每一层中（除输入层和输出层）的每一个节点都要连接到前/后层中的每个节点。

理解了这一点，我们就能进入下一个主题，即神经网络优化算法（误差最小化）。在这里，我们主要介绍最简单的梯度下降。

批量梯度下降和随机梯度下降

梯度下降一般有三种形式：批量梯度下降法（Batch Gradient Descent）随机梯度下降法（Stochastic Gradient Descent）和小批量梯度下降法（Mini-Batch Gradient Descent）。由于本文为入门向，我们就先来了解满批量梯度下降法（Full BGD）和随机梯度下降法（SGD）。

这两种梯度下降形式使用的是同一种更新算法，它们通过更新MLP的权值来达到优化网络的目的。不同的是，满批量梯度下降法通过反复更新权值来使误差降低，它的每一次更新都要用到所有训练数据，这在数据量庞大时会耗费太多时间。而随机梯度下降法则只抽取一个或多个样本（非所有数据）来迭代更新一次，较之前者，它在耗时上有不小的优势。

让我们来举个例子：假设现在我们有一个包含10个数据点的数据集，它有w1、w2两个权值。

• 满批量梯度下降法：你需要用10个数据点来计算权值w1的变化情况Δw1，以及权值w2的变化情况Δw2，之后再更新w1、w2。

• 随机梯度下降法：用1个数据点计算权值w1的变化情况Δw1和权值w2的变化情况Δw2，更新w1、w2并将它们用于第二个数据点的计算。

神经网络构建过程详解

在这一节中，让我们来看看神经网络（MLP包含隐藏层，类似上图架构）的具体构建方法。

如上图所示，我们的神经网络共有3层，它的思路可以被大致概括为：

第0步 确定输入和输出

我们定义：

• x为输入矩阵；

• y为输出矩阵。

第1步 用一个随机值初始化网络的权值和bias（只在开始时使用，下一次迭代我们会用更新后的值）

我们定义：

• wh为隐藏层的权值矩阵；

• bh为隐藏层的bias矩阵；

• wout为输出层的权值矩阵；

• bout为输出层的bias矩阵。

第2步 将输入矩阵和权值的矩阵点乘积分配给输入和隐藏层之间的边缘，再加上隐藏层的bias形成相应输出，这个过程被称作线性变换

hiddenlayerinput = matrixdotproduct（X，wh）+bh

第3步 引入激活函数（Sigmoid）执行非线性变换，Sigmoid输出1/(1+exp(-x))

hiddenlayeractivations = sigmoid（hiddenlayer_input）

第4步 对隐藏层进行线性变换（在原矩阵点乘积的基础上乘以新权值矩阵并加上输出层bias），使用激活函数，并预测输出

outputlayerinput = matrixdotproduct (hiddenlayeractivations × wout ) + bout output = sigmoid(outputlayer_input)

以上步骤即为“前向传播”。

第5步 将预测值与实际值相比较，并计算误差E（Actual-Predicted）的梯度，它是一个平方误差函数((y-t)^2)/2（衡量期望误差的一个常见做法是采用平方误差测度）

E=y–output

第6步 计算隐藏层和输出层神经元的斜率/梯度（对每个神经元每一层的非线性激活函数x求导），Sigmoid的梯度会返回为x(1–x)

slopeoutputlayer = derivativessigmoid(output) slopehiddenlayer = derivativessigmoid(hiddenlayer_activations)

第7步 用误差E的梯度和输出层激活函数梯度计算输出层的变化因子（delta）

doutput = E × slopeoutput_layer

第8步 这时，误差E已经回到神经网络中，也就是在隐藏层中。为了计算它的梯度，我们需要用到输出变化因子delta中的点和隐藏层输出层之间的权重参数

Errorathiddenlayer = matrixdotproduct（doutput，wout.Transpose）

第9步 计算隐藏层的变化因子（delta），将得到的误差和隐藏层激活函数导数相乘

dhiddenlayer = Errorathiddenlayer × slopehiddenlayer

第10步 更新输出层和隐藏层的权值：可以用训练样本的误差更新权值

• wout = wout + matrixdotproduct（hiddenlayeractivations.Transpose，doutput）× learning_rate

• wh = wh + matrixdotproduct（X.Transpose，dhiddenlayer）× learningrate

• 学习率（learning rate）：权值更新速率由自定义超参数学习率决定。

第11步 更新输出层和隐藏层的bias：神经网络中的bias可以由神经元中的累积误差求导更新

• bias at outputlayer =bias at outputlayer + sum of delta of outputlayer at row-wise × learningrate

• bias at hiddenlayer =bias at hiddenlayer + sum of delta of outputlayer at row-wise × learningrate

即：

• bh = bh + sum(dhiddenlayer, axis=0)×learningrate

• bout = bout + sum(doutput, axis=0)×learningrate

我们称5—11为“反向传播”。

我们把一个前向传播和一个反向传播的迭代成为一个训练周期。正如我在前文中提到的，如果我们再进行训练，那更新后的权值和bias就会用于新一次前向传播。

神经网络构建过程的可视化

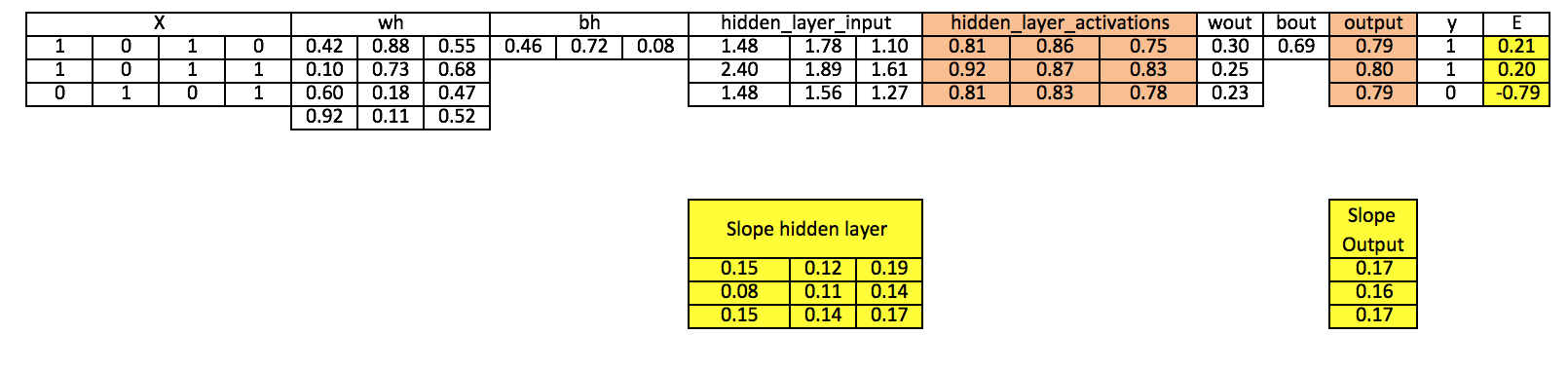
我会在这一节中用图表形式重新介绍上一节的内容，以帮助入门者更好地了解神经网络（MLP）的工作方法。

注意：

• 为了更好的呈现效果，我只保留了2位或3位小数；

• 黄色单元格表示当前活动的神经元（单元、节点）；

• 橙色单元格表示用于更新当前单元格值的输入。

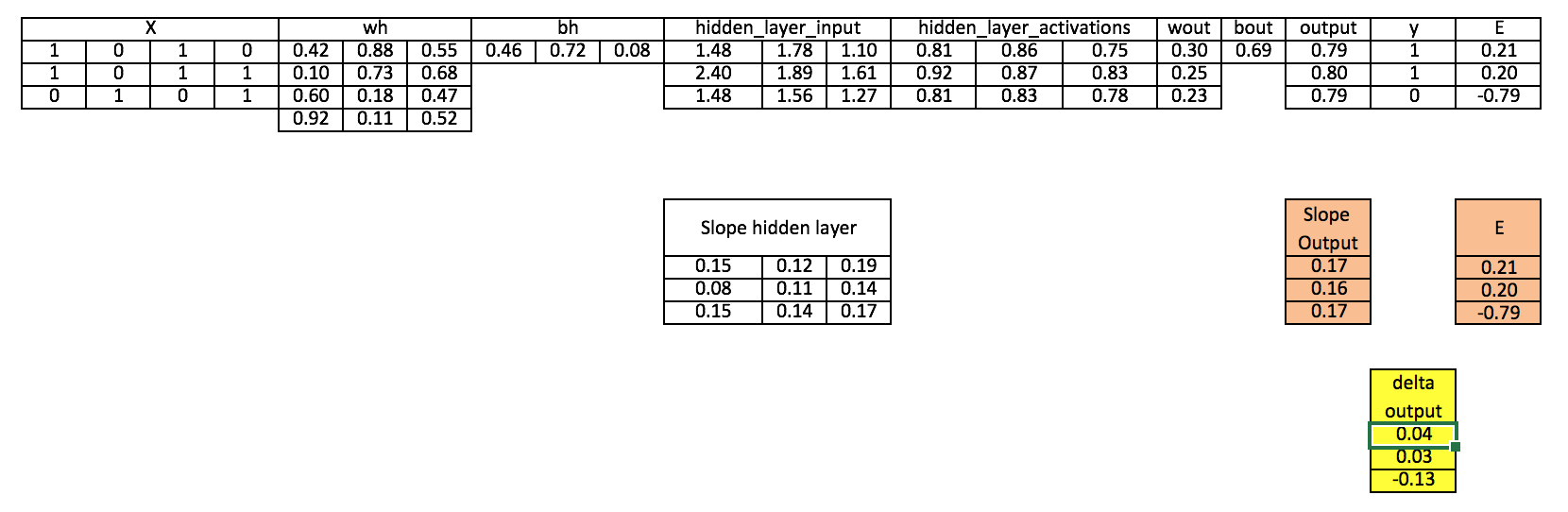
第0步 读取输入和输出

第1步 用随机值初始化权值和bias

第2步 计算隐藏层输入

hiddenlayerinput = matrixdotproduct（X，wh）+ bh

第3步 对隐藏层的线性输入执行非线性变换（激活函数）

hiddenlayeractivations = sigmoid（hiddenlayer_input）

第4步 在输出层对已经执行了线性、非线性变换的隐藏层使用激活函数

outputlayerinput = matrixdotproduct（hiddenlayeractivations × wout）+ bout output = sigmoid（outputlayer_input）

第5步 计算输出层误差E的梯度

E = y-output

第6步 计算输出层和隐藏层的梯度

Slopeoutputlayer= derivativessigmoid(output) Slopehiddenlayer = derivativessigmoid(hiddenlayer_activations)

第7步 计算输出层的delta

doutput = E × slopeoutput_layer*lr

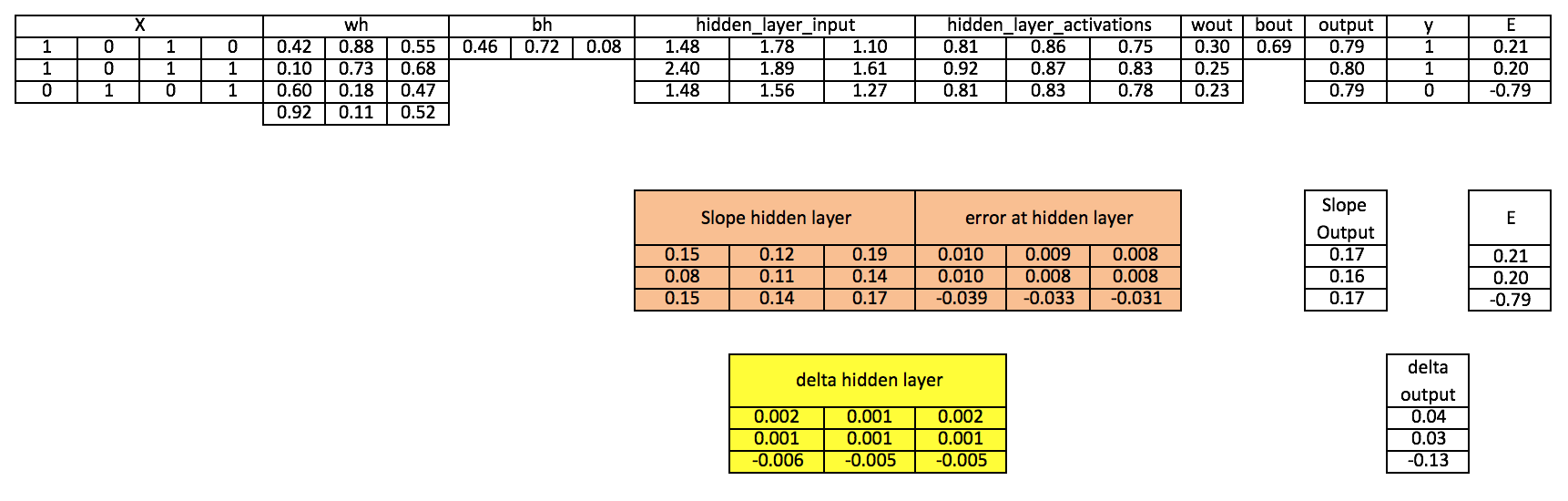
第8步 计算隐藏层的误差

Errorathiddenlayer = matrixdotproduct(doutput, wout.Transpose)

第9步 计算隐藏层的delta

dhiddenlayer = Errorathiddenlayer × slopehiddenlayer

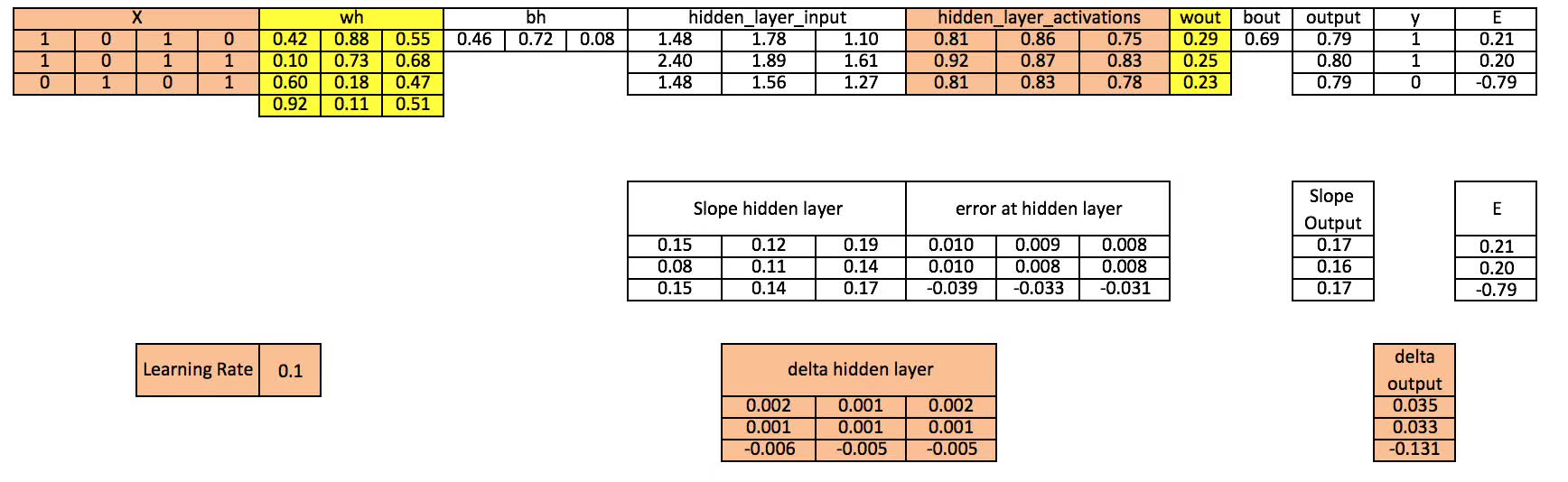
第10步 更新输出层和隐藏层的权值

wout = wout + matrixdotproduct(hiddenlayeractivations.Transpose, doutput)×learningrate wh = wh+ matrixdotproduct(X.Transpose,dhiddenlayer)×learning_rate

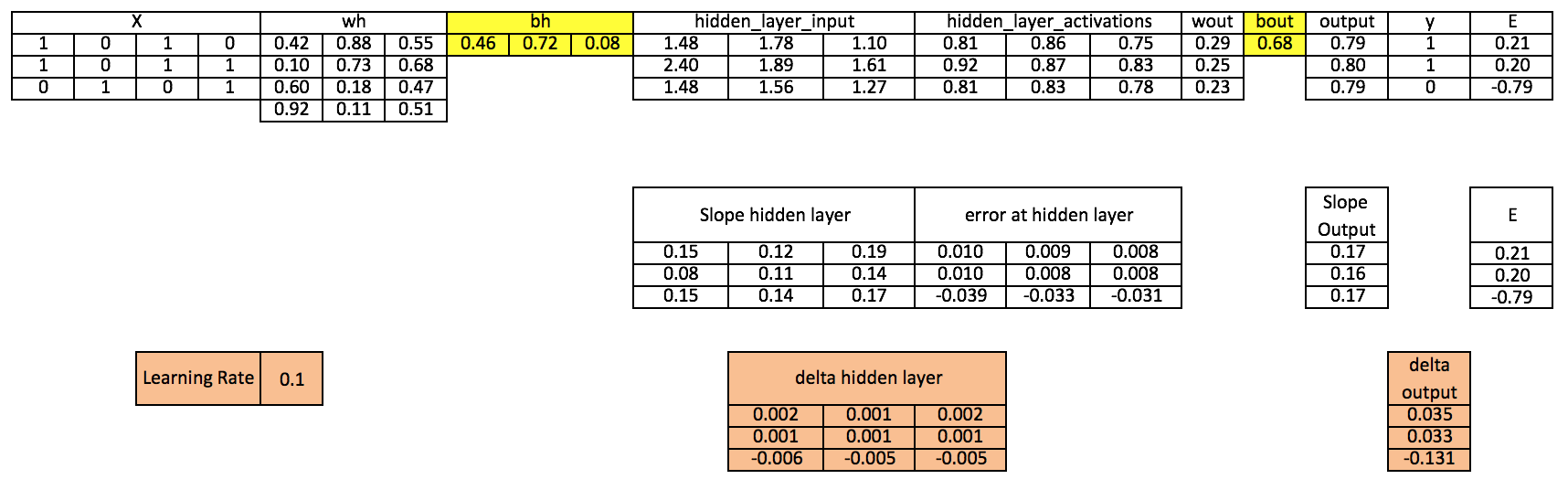
第11步 更新输出层和隐藏层的bias

bh = bh + sum(dhiddenlayer, axis=0) ×learningrate bout = bout + sum(doutput, axis=0)×learningrate

由表格数据可以看出，由于我们只进行了一次迭代，因此预测值和实际值的误差还相对过大。如果我们多次训练模型，那它们最终将趋于靠近。事实上，我之后已经对这个模型进行了上千次迭代，最后得到了和目标值很相近的结果：[[ 0.98032096] [ 0.96845624] [ 0.04532167]]。

如何用Numpy实现NN（Python）

import numpy as np
#Input array
X=np.array([[1,0,1,0],[1,0,1,1],[0,1,0,1]])
#Output
y=np.array([[1],[1],[0]])
#Sigmoid Function
def sigmoid (x):
return 1/(1 + np.exp(-x))
#Derivative of Sigmoid Function
def derivatives_sigmoid(x):
return x * (1 - x)
#Variable initialization
epoch=5000 #Setting training iterations
lr=0.1 #Setting learning rate
inputlayer_neurons = X.shape[1] #number of features in data set
hiddenlayer_neurons = 3 #number of hidden layers neurons
output_neurons = 1 #number of neurons at output layer
#weight and bias initialization
wh=np.random.uniform(size=(inputlayer_neurons,hiddenlayer_neurons))
bh=np.random.uniform(size=(1,hiddenlayer_neurons))
wout=np.random.uniform(size=(hiddenlayer_neurons,output_neurons))
bout=np.random.uniform(size=(1,output_neurons))
for i in range(epoch):
#Forward Propogation
hidden_layer_input1=np.dot(X,wh)
hidden_layer_input=hidden_layer_input1 + bh
hiddenlayer_activations = sigmoid(hidden_layer_input)
output_layer_input1=np.dot(hiddenlayer_activations,wout)
output_layer_input= output_layer_input1+ bout
output = sigmoid(output_layer_input)
#Backpropagation
E = y-output
slope_output_layer = derivatives_sigmoid(output)
slope_hidden_layer = derivatives_sigmoid(hiddenlayer_activations)
d_output = E * slope_output_layer
Error_at_hidden_layer = d_output.dot(wout.T)
d_hiddenlayer = Error_at_hidden_layer * slope_hidden_layer
wout += hiddenlayer_activations.T.dot(d_output) *lr
bout += np.sum(d_output, axis=0,keepdims=True) *lr
wh += X.T.dot(d_hiddenlayer) *lr
bh += np.sum(d_hiddenlayer, axis=0,keepdims=True) *lr
print output

如何用R语言实现NN

# input matrix
X=matrix(c(1,0,1,0,1,0,1,1,0,1,0,1),nrow = 3, ncol=4,byrow = TRUE)
# output matrix
Y=matrix(c(1,1,0),byrow=FALSE)
#sigmoid function
sigmoid<-function(x){
1/(1+exp(-x))
}
# derivative of sigmoid function
derivatives_sigmoid<-function(x){
x*(1-x)
}
# variable initialization
epoch=5000
lr=0.1
inputlayer_neurons=ncol(X)
hiddenlayer_neurons=3
output_neurons=1
#weight and bias initialization
wh=matrix( rnorm(inputlayer_neurons*hiddenlayer_neurons,mean=0,sd=1), inputlayer_neurons, hiddenlayer_neurons)
bias_in=runif(hiddenlayer_neurons)
bias_in_temp=rep(bias_in, nrow(X))
bh=matrix(bias_in_temp, nrow = nrow(X), byrow = FALSE)
wout=matrix( rnorm(hiddenlayer_neurons*output_neurons,mean=0,sd=1), hiddenlayer_neurons, output_neurons)
bias_out=runif(output_neurons)
bias_out_temp=rep(bias_out,nrow(X))
bout=matrix(bias_out_temp,nrow = nrow(X),byrow = FALSE)
# forward propagation
for(i in 1:epoch){
hidden_layer_input1= X%*%wh
hidden_layer_input=hidden_layer_input1+bh
hidden_layer_activations=sigmoid(hidden_layer_input)
output_layer_input1=hidden_layer_activations%*%wout
output_layer_input=output_layer_input1+bout
output= sigmoid(output_layer_input)
# Back Propagation
E=Y-output
slope_output_layer=derivatives_sigmoid(output)
slope_hidden_layer=derivatives_sigmoid(hidden_layer_activations)
d_output=E*slope_output_layer
Error_at_hidden_layer=d_output%*%t(wout)
d_hiddenlayer=Error_at_hidden_layer*slope_hidden_layer
wout= wout + (t(hidden_layer_activations)%*%d_output)*lr
bout= bout+rowSums(d_output)*lr
wh = wh +(t(X)%*%d_hiddenlayer)*lr
bh = bh + rowSums(d_hiddenlayer)*lr
}
output

反向传播算法的数学原理（选读）

设Wi为输入层与隐藏层之间的权值，Wh为隐藏层和输出层之间的权值。

h=σ(u)= σ (WiX)，其中h是u的函数，u是Wi和x的函数。这里我们将激活函数表示为σ。

Y=σ(u')=σ(Whh)，其中Y是u'的函数，u'是Wh和h的函数。

利用上述等式，我们可以计算偏导数。

我们需要计算∂E/∂Wi和∂E/∂Wh，其中前者是改变输入层、隐藏层之间权值造成的误差（E）的变化，后者是改变隐藏层、输出层之间权值造成的误差（E）的变化。

为了得出这两个偏导数，我们需要用到链式法则，因为E是Y的函数，Y是u'的函数，而u'是Wi的函数。

让我们结合它们的关系来计算梯度：

∂E/∂Wh = (∂E/∂Y).( ∂Y/∂u’).( ∂u’/∂Wh)……（1）

已知误差E=((Y-t)^2)/2，可得(∂E/∂Y)= (Y-t)。

由于激活函数σ求导后的形式是σ(1-σ)，因此

(∂Y/∂u’)= ∂( σ(u’)/ ∂u’= σ(u’)(1-σ(u’))

但是因为σ(u’)=Y，所以

(∂Y/∂u’)=Y(1-Y)

现在我们就能得到( ∂u’/∂Wh)= ∂( Whh)/ ∂Wh = h

把这个等式带入式（1）可得

∂E/∂Wh = (Y-t). Y(1-Y).h

现在我们已经得出了隐藏层和输出层之间的梯度，是时候该计算输入层和隐藏层之间的梯度了。

∂E/∂Wi =(∂E/∂h). (∂h/∂u).( ∂u/∂Wi)

但是，(∂E/∂h) = (∂E/∂Y).( ∂Y/∂u’).( ∂u’/∂h)也同样成立，将这个式子带入上式后，

∂E/∂Wi =[(∂E/∂Y).( ∂Y/∂u’).( ∂u’/∂h)]. (∂h/∂u).( ∂u/∂Wi)……（2）

可能会有人有一位，为什么我们要先计算隐藏层和输出层之间的梯度呢？这个问题的解答就在式（2）中。我们可以发现，由于之前我们已经先计算了∂E/∂Y和∂Y/∂u’，在进行之后的计算时，我们无需进行大量重复计算，这大大节约了资源占用和计算时间，提高了整体效率。这也是这个算法被称为反向传播算法的原因。

解下来让我们计算式（2）中的未知导数。

∂u’/∂h = ∂(Whh)/ ∂h = Wh

∂h/∂u = ∂( σ(u)/ ∂u= σ(u)(1- σ(u))

因为σ(u)=h，所以

(∂Y/∂u)=h(1-h)

我们可以得到∂u/∂Wi = ∂(WiX)/ ∂Wi = X

将它代入式（2）我们可得梯度

∂E/∂Wi = [(Y-t). Y(1-Y).Wh].h(1-h).X

既然我们已经计算得到两个梯度，那神经网络的权值就可以更新为

Wh = Wh + η . ∂E/∂Wh

Wi = Wi + η . ∂E/∂Wi

其中η表示学习率。

这里我们可以再一次回到这个算法的命名上。通过对比∂E/∂Wh和∂E/∂Wi的最终形式我们可以发现，预测值和实际值的误差(Y-t)在权值更新的过程中被作为了输入层。

那这些数学计算是怎么和代码对应的呢？

hiddenlayer_activations = H
E = Yt
Slope_output_layer = Y（1-Y）
lr =η
slope_hidden_layer = h（1-h）
wout = W<sub>h</sub>

论智补充

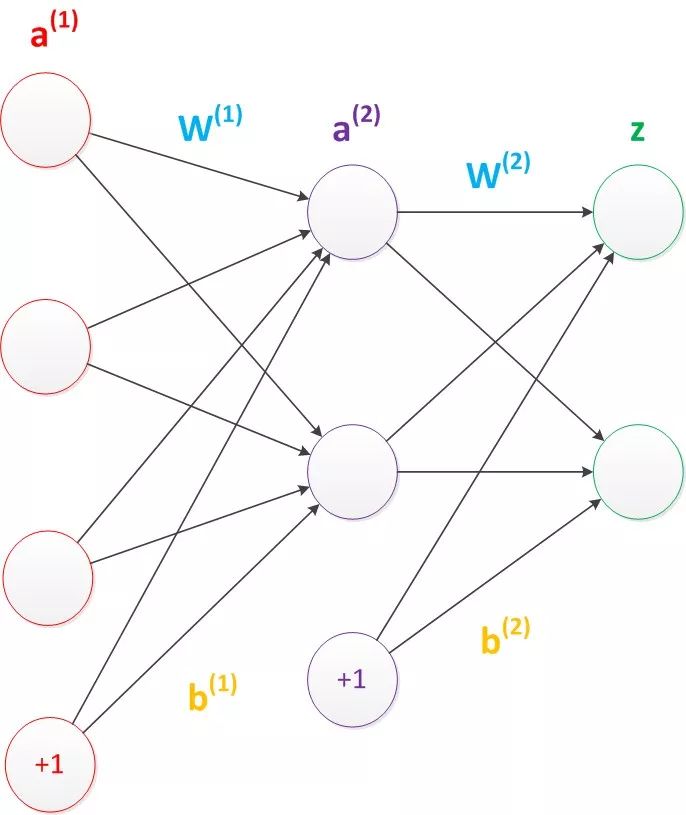
本文以神经网络中最基础的两层神经网络作为讲解对象，虽然内容已经很翔实，但为了更形象地解释输入、输出、权值、bias等概念在图中的位置，论智君在文末为读者做一些基础知识补充。

上图是一个简单的两层神经网络，它由一些圆形和向量组成，其中的圆圈就是我们说的神经元，有时也称单元（unit）和节点（node），它主要起到计算和储存作用，因此其实发挥重要作用的是图中的各条带箭头的线。

文章中涉及大量“输入层隐藏层之间的权值”“隐藏层输出层之间的权值”的表述，这些都可以从图片中获得直观感受。而我们反复提起的偏置项bias在上图中也有所展示。理论上，bias是个储存值永远为1的单元，它出现在除了输入层之外的所有层，与后一层的所有节点都有连接。神经网络结构图一般不会把它明确画出来，但我们应该知道它是存在的。

本文把多处神经网络都注释为MLP，并详细介绍了多层感知器的设计演变。需要注意的是，MLP曾经就指代神经网络，但是它表示的是两层神经网络，即包含一个输入层、隐藏层、输出层的神经网络，一般不能被用来表示层数非常深的神经网络。

论智也沿用了损失的英文原型loss，区别于error误差。另外会有人把loss译为残差、代价，尤其是在谈及loss function的时候，它们其实是一种东西。

最后再提一点阈值和参数。文章在介绍bias时用了它的英文单词，没有用它的译名偏置项、阈值，这是为了防止误读，尤其是阈值，它容易与案例中的约束条件混淆。事实上，bias作为阈值最生动的体现是在图像上，它能限制曲线的峰值区间，具体可以Google相关图片。而本文尽量避免了“参数”这个词的使用，因为一般而言，神经网络参数就是指训练得到的权值和bias，把这个概念用于任何一方都是不合理的，它和其他机器学习方法中的参数也不是一个概念，在阅读其他原创、翻译内容时，希望读者能擦亮双眼。

原文地址：www.analyticsvidhya.com/blog/2017/05/neural-network-from-scratch-in-python-and-r/