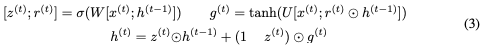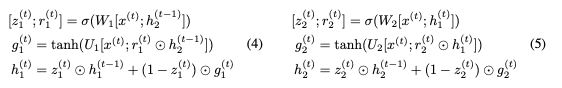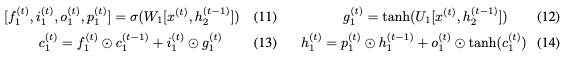【NIPS 2018】多伦多大学提出可逆RNN:内存大降,性能不减!
新智元报道
新智元报道
来源:arXiv
编辑:肖琴
【新智元导读】多伦多大学的研究人员提出Reversible RNN,一种可以减少RNN训练时内存需求的新方法,在保留模型性能的同时,将激活内存成本降低了10-15倍。
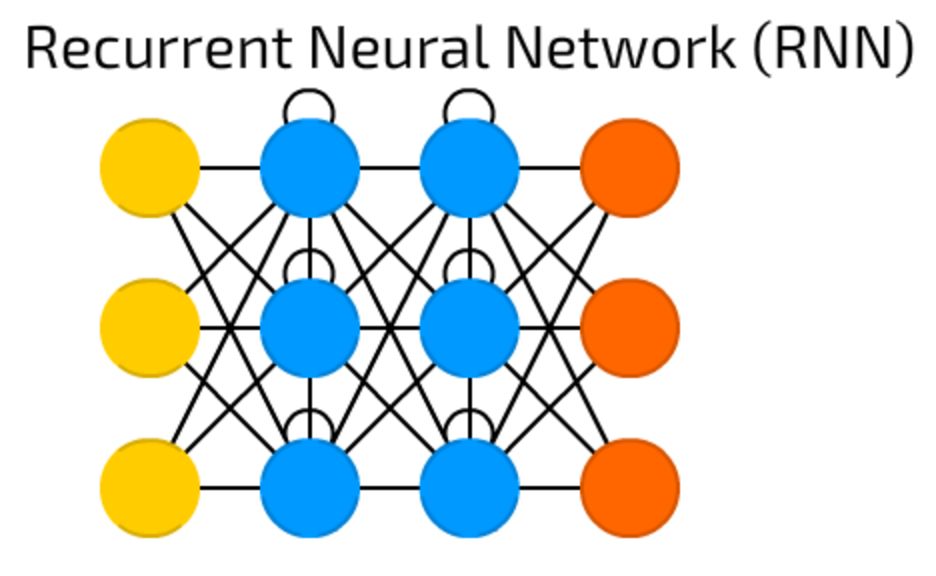
循环神经网络(RNN)在处理序列数据方面能有很好的性能,但在训练时需要大量内存,限制了可训练的RNN模型的灵活性。
近日,多伦多大学Vector Institute的研究人员提出Reversible RNN,描述了一种可以减少RNN训练时内存需求的新方法。论文题为Reversible Recurrent Neural Networks,已被NIPS 2018接收。
https://arxiv.org/pdf/1810.10999.pdf
可逆RNN(Reversible RNN)是指网络中hidden-to-hidden的转换可以逆向进行的RNN,这就提供了一个减少训练的内存需求的路径,因为隐藏状态不需要存储,而是可以在反向传播期间重新计算。
这篇论文先证明了完全可逆的RNN(perfectly reversible RNNs),即不需要存储隐藏的激活,在根本是受到限制的,因为它们不能忘记隐藏状态的信息。
然后,论文提出一种存储少量bits的方案,以允许在遗忘时实现完美的逆转。
这一方法实现了与传统模型相当的性能,同时将激活内存成本降低了10-15倍。
研究人员将这一方法扩展到基于注意力的sequence-to-sequence模型,实验证明能它能保持性能,同时在encoder中将激活内存成本降低了5-10倍,在decoder中降低了10-15倍。
用于构建RevNets的技术可以与传统的RNN模型结合,产生reversible RNN。在本节中,我们提出了GRU和LSTM的可逆版本。
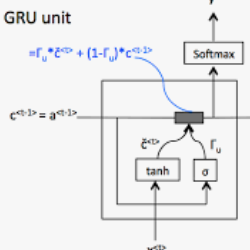
Reversible GRU
让我们首先回顾一下用于计算下一个隐藏状态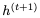
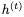

这里,⊙表示elementwise乘法。为了使这个更新可逆,我们将隐藏状态h分成两组,
注意,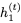

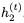
对于i = 1,2,
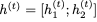
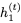


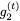
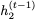
Reversible LSTM
接下来我们构建一个reversible LSTM。LSTM将隐藏状态分离为输出状态h和单元状态c。更新方程是:
我们不能直接应用可逆技术,因为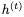
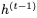
使用
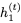
我们已经证明,通过确保不丢弃任何信息,可以构建具有有限精度的reversible RNN。
但是,对于语言建模等任务,我们还是无法找到能获得可接受性能的架构。
我们认为这是由于无遗忘可逆模型(no-forgetting reversible models)的基本限制导致的:如果任何隐藏状态都不能被遗忘,那么任何给定时间步长的隐藏状态必须包含足够的信息来重建所有先前的隐藏状态。因此,在一个时间步长上,存储在隐藏状态中的任何信息都必须保留在所有未来的时间步长,以确保精确的重构,从而超过了模型的存储容量。
图1:在重复任务上展开完全可逆模型的反向计算,得到sequence-to-sequence计算。左:重复任务本身,其中模型重复每个输入标记。 右:展开逆转。模型有效地使用最终隐藏状态来重建所有输入tokens,这意味着整个输入序列必须存储在最终隐藏状态中。
我们通过考虑一个基本的序列学习任务,即重复任务,来说明这个问题。在这个任务中,RNN被输入一个离散token的序列,并且必须在随后的时间步长中简单地重复每个token。
普通的RNN模型只需要少量的隐藏单元就可以轻松解决这个任务,因为它不需要建模长距离依赖关系。但请考虑一个完全可逆的模型如何执行重复任务。
展开反向计算,如图1所示,显示了sequence-to-sequence的计算,其中编码器和解码器权重相关联。编码器接收token并产生最终隐藏状态。解码器使用该最终隐藏状态以反向顺序产生输入序列。
我们通过实验证实,容量有限的NF-RevGRU和NF-RevLSM网络无法解决重复任务。
由于No Forgetting不可能,我们需要探索实现可逆性的第二种可能:在正向运算期间存储隐藏状态丢失的信息,然后在反向计算终恢复它。
我们研究了fractional forgetting,即允许遗忘一小部分bits。
算法1描述了可逆乘法的完整过程。
我们在两个标准RNN任务上评估了可逆模型的性能:语言建模和机器翻译。我们希望确定使用我们开发的技术可以节省多少内存,这些节省跟使用理想缓冲区可能节省的内存有可比性吗,以及这些内存节省是否以降低性能为代价。
表1:Penn TreeBank词级语言建模上的验证困惑度(内存节省)。当遗忘被限制为每个timestep 每个隐藏单元2、3和5bits,以及没有限制的情况下的结果。
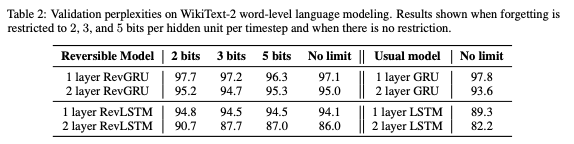
表2:WikiText-2单词级语言建模的验证困惑度。当遗忘被限制为每个timestep 每个隐藏单元2、3和5bits,以及没有限制的情况下的结果。
表3:具有不同遗忘限制时Multi30K数据集上的性能。P表示测试BLEU scores; M表示训练期间编码器的平均内存节省。
总的来说,虽然Emb attention实现了最佳的内存节省,但Emb + 20H在性能和内存节省之间实现了最佳平衡。
具有Emb + 20H attention且遗忘最多2bits的RevGRU实现了34.41的test BLEU score,优于标准GRU,同时分别在编码器和解码器中将激活内存要求降低了7.1倍和14.8倍。
具有Emb + 20H attention且遗忘最多3bits的RevLSTM的test BLEU score为37.23,优于标准LSTM,同时分别在编码器和解码器中将激活内存要求降低了8.9倍和11.1倍。
baseline GRU和LSTM模型的测试BLEU分数分别是16.07和22.35。RevGRU的测试BLEU得分为20.70,优于GRU,同时分别在编码器和解码器中节省内存7.15倍和12.92倍。RevLSTM得分为22.34,与LSTM相比,分别在编码器和解码器中节省了8.32倍和6.57倍的内存。两种可逆模型都被限制为最多遗忘5 bits。
论文地址:
https://arxiv.org/pdf/1810.10999.pdf
新智元AI WORLD 2018
世界人工智能峰会全程回顾
新智元于9月20日在北京国家会议中心举办AI WORLD 2018世界人工智能峰会,邀请机器学习教父、CMU教授 Tom Mitchell,迈克思·泰格马克,周志华,陶大程,陈怡然等AI领袖一起关注机器智能与人类命运。
全程回顾新智元 AI World 2018 世界人工智能峰会盛况:
爱奇艺
上午:https://www.iqiyi.com/v_19rr54cusk.html
下午:https://www.iqiyi.com/v_19rr54hels.html
新浪:http://video.sina.com.cn/l/p/1724373.html