Distributional Soft Actor-Critic (DSAC)强化学习算法的设计与验证

2020 年 8 月 11 日 深度强化学习实验室

深度强化学习实验室

作者: DeepRL

来源：清华大学

一、摘要

近年来，强化学习在围棋、游戏等领域的应用取得巨大成功。然而，现有算法在学习过程中值函数的近似误差会造成严重的过估计问题，导致策略性能极大地降低。智能驾驶课题组（iDLab）提出一种可减少过估计的Distributional Soft Actor-Critic(DSAC)算法，通过学习连续状态-动作回报分布(state-action return distribution)来动态调节Q值的更新过程，并证明引入该分布降低过估计的原理。本文基于异步并行计算框架PABAL来实施DSAC算法，Mujoco环境的验证表明：相比于目前最流行的强化学习算法，如：SAC、TD3、DDPG等，所提出的DSAC算法在不引入额外值网络或者策略网络的前提下能够更加有效地降低Q值的估计误差，并在各项任务中获得最好的性能。

二、介绍

从Q-learning算法开始，不少研究者均发现强化学习存在严重的过估计问题。由于Q学习算法中不断的对下一时刻的状态值进行max操作，任何引起的Q值误差的因素如环境中的噪声、网络的近似误差都会导致对Q值的偏高的估计，即过估计。而在时间差分学习中，这种估计误差又会被进一步放大，因为后面状态的过估计误差在更新过程中又会进一步传播到前面的状态中。为了解决过估计问题，研究者提出著名的Double DQN算法及诸多以其为基础的变种，但是此类方法只能解决离散动作空间的问题。对于连续控制任务，以Clipped Double Q-learning为基础的TD3和SAC等算法则面临着低估问题。本文首次从理论层面发现和论证了分布式回报函数的学习降低Q值过估计的原理，并将分布式回报学习嵌入到Maximum Entropy架构中从而提出了面向连续控制任务的DSAC算法。一篇近期的Nature论文指出，人类大脑给出的奖励并不是一个单一的信号，而是基于某种概率分布，这也显示了分布式回报机制设计的合理性和巨大潜力。同时，与现有Distributional RL算法（如C51，IQN，D4PG等）不同的是，DSAC可以直接学习一个连续型分布式值函数，这避免了离散分布学习带来的人工设计分割区间需求。

三、Distributional RL 框架

DSAC是基于Maximum Entropy架构设计的，该学习过程不仅试图最大累积的回报，同时最大化策略的熵以提高策略的探索性：

其中，为策略下状态动作对的分布, 为策略的熵, 为每一步的奖励，为折扣因子，为熵的系数。我们用定义考虑了熵之后的回报, 也被称为soft return, 则对应的soft Q值为：

此版本下的最优策略的求解仍然由策略评估和策略提升两步构成，在策略迭代中，基于以下的贝尔曼自洽算子来更新值函数：

策略提升环节通过最大化值函数对策略进行更新：

以上两步交替迭代直到达到最终的最优策略。

Distributional RL直接对回报分布进行建模，而并非学习其期望值（Q值），其定义为：

此时其均值为Q函数：

假设return的分布为，那么在distributional RL 框架下策略评估这一步变成了评估当前策略下return的分布，其贝尔曼算子为：

很显然，上式等号两端都是分布，因此表示两个分布具有相同的概率形式。而此时的策略提升环节仍然和Maximum Entropy RL类似，我们把这种结合最大熵和分布式回报的策略迭代称之为‘Distributional Soft Policy Iteration (DSPI)’,并且证明DSPI也会收敛到最优的策略。

四、减小过估计的原理

本节对return distribution学习的过估计误差进行定量分析。为方便起见，假设熵的权重系数为0。在Q学习算法中，定义其目标函数值为 , 每一步Q值的更新都是最小化目标值和当前值的平方误差，即：

其中为学习率。但是，以上更新的Q值和真实的Q值总会存在一定的误差：

其中，误差是零均值的并且和、独立。此时，真实的参数值为：

其中，

. 那么，此时的估计误差为：

其中，

可以看到，总是成立，因此这是一个过估计的误差。

下面分析引入分布式return之后对过估计的影响，假设return服从高斯分布，其均值和方差可以由两个独立的函数和表示，其中，和是函数的参数，即. 同样，需要假设目标分布为. 接下来可以证明此时的过估计误差：

可以看到，此时的过估计误差随着的增大呈平方下降趋势。另一方面，通常正比于系统的不确定性，回报函数的随机性以及后续return分布的随机性，这些不确定性和随机性越显著，那么就越大，分布式回报学习对误差的降低作用也更加显著。同时，如果则有。通过方差剪枝技术和reward缩放技术，是很容易得到满足的。

五、DSAC算法设计

在前文中，我们提出了DSPI的框架并证明了策略的收敛性，本节以此为基础提出一种具体的算法：Distributional Soft Actor-Critic,简写为DSAC。考虑return和策略服从参数化的高斯分布和 , 它们的均值和方差都由神经网络拟合。

在策略评估阶段，我们选择KL散度为分布距离的度量，优化当前策略对应的return的分布：

关于参数的梯度为：

以上梯度公式面临两个问题：当分布的标准差和时，将分别发生梯度爆炸或消失。这里我们采用截断技术（clip）解决这一问题，将标准差限制在一个合理范围内，同时为了防止目标分布变化过大造成学习的不稳定，将目标分布限制在当前return分布的期望附近：

其中为一个常数，称作截断边界。另外，目标网络采用常见的slow-moving更新方式：

在策略改进阶段，可以直接最大化soft Q值：

为了减小策略的方差，我们使用重参数化技术求解策略的梯度。如果中显含 , 则可以将随机动作表示为：

这里是从某个分布采样的辅助变量，此时梯度为：

如果中不显含，还需要对return的分布进行重参数化：

此时得到的梯度为：

此外，熵系数更新方式参考了SAC论文的更新：

整个算法伪代码如图1所示：

图1 DSAC算法伪代码

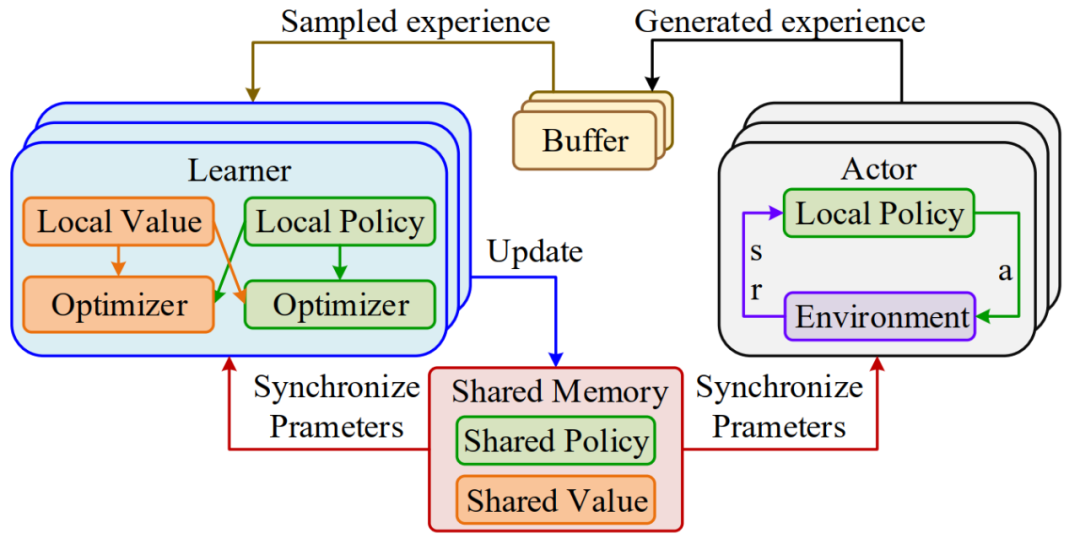
本文基于parallel asynchronous buffer-actor-learner architecture (PABAL)这一异步并行计算架构（如图2）来部署各强化学习算法，以提高采样、探索和更新效率。每个actor异步地与环境交互并将产生的经验数据随机发送至buffer，buffer随机选取经验并发送至随机的learner计算梯度，更新共享值网络与策略网络参数。为了方便对比，论文中所有的算法均在PABAL架构下实现。

图2 PABAL架构

六、实验结果

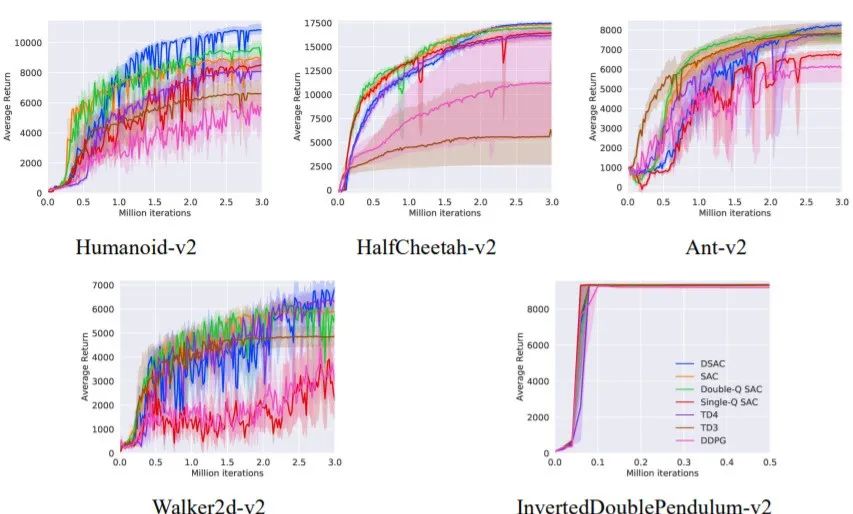
实验任务为经典的MuJoCo连续控制任务平台，共做了Humanoid-v2、HalfCheetah-v2、Ant-v2、Walker2d、InvertedDoublePendulum-v2等5个任务。比较的算法包括DDPG，TD3与SAC,以及本文提出的SAC两种变体Double-Q SAC和Single-Q SAC。另外，我们将传统TD3算法引入分布式return提出一种新的算法，称为TD4算法。所有算法采用相同的神经网络结构、训练超参数、PABAL进程数与输入输出。绘制训练曲线如图3所示，实验结果表明本文所提出的DSAC算法在5个MuJoCo连续控制任务中均能取得最好的效果。此外，TD4的表现超越了基础版本TD3与DDPG，也验证了分布式return的引入也能提升确定性策略的性能。DSAC和SAC的控制效果比较见视频。由于mujoco环境的reward往往与智能体速度成正比，DSAC控制下的智能体具有更好的行走姿态因此其回报更高。

图3 MuJoCo连续控制任务训练曲线（实线表示均值，阴影区域表示5次运行95%置信区间）

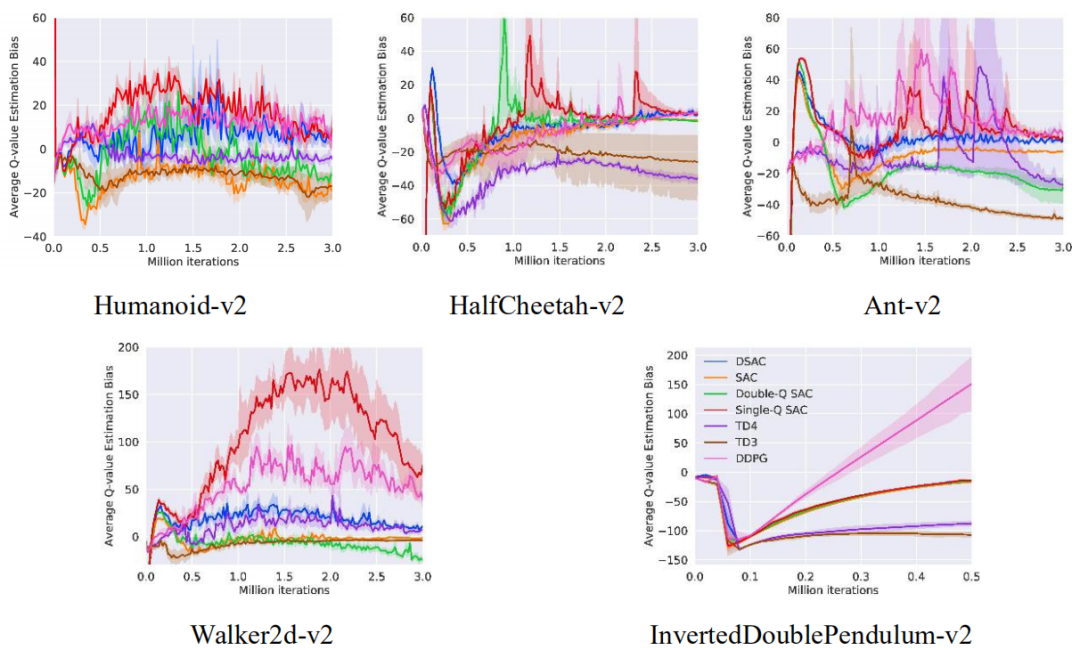
本文进一步比较了不同算法对Q值估计的误差，结果如图4所示。基于时间差分学习的算法（如DDPG、Single-Q SAC）容易产生过估计，而基于Clipeed Double Q-learning的算法（如SAC、TD3）通常导致低估。从综合表现来看，DSAC算法的估计偏差介于过估计算法与低估算法之间，这也是其性能表现最优的原因。

图4 MuJoCo练习控制任务的平均Q值估计偏差曲线（实线表示均值，阴影区域表示5次运行的95%置信区间）

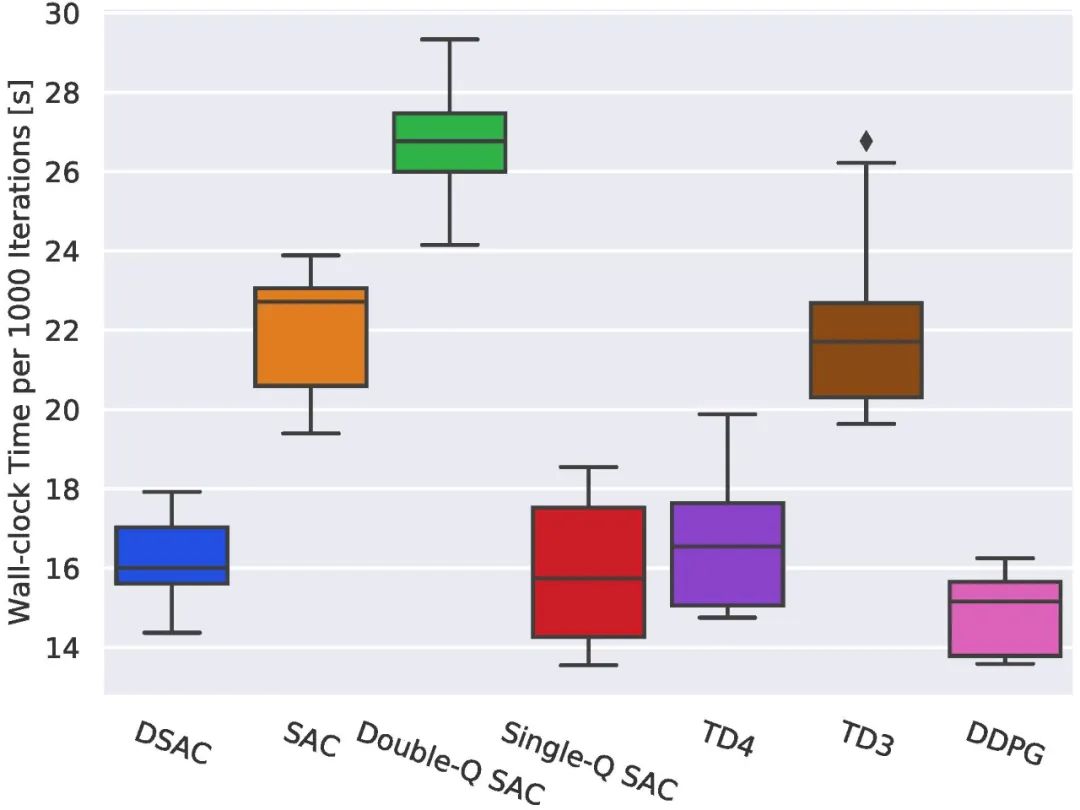
最后，我们也比较了不同算法的迭代效率，结果如图5所示。结果表明DSAC、TD4、Single -QSAC、DDPG每1000次迭代的时钟时间远小于SAC、TD3与Double-Q SAC。这是因为基于分布式回报的算法不需要引入额外值网络/策略网络以减少过估计，其网络的数目要更少，因此相同迭代的计算时间更少。

图5 各算法迭代时间效率对比

总结而言，DSAC在不需要引入额外值网络和策略网络的前提下，可以很好地抑制过估计误差并提高策略性能。

7、结论

本文提出了一种用于连续控制任务的强化学习算法—DSAC（Distributional Soft Actor-Critic），其优势在于减少Q值的过估计并显著改进策略的性能。首先，证明了强化学习中引入分布式回报可显著降低Q值的过估计误差，并定量表明此误差与分布的方差呈反比关系。其次，通过在现存的最大熵框架中引入分布式回报，提出了DSPI过程并证明该过程能够收敛到最优策略。最后，论文以DSPI为理论基础提出DSAC算法，该算法能够直接学习连续型回报分布函数。此外，还提出一种适用于并行计算PABAL架构，并使用典型的MuJoCo任务进行对比实验。结果表明DSAC在所有的任务中表现最佳或与最佳算法接近，并且DSAC每次迭代的平均时间仅为SAC算法的70%。后续我们团队将这一工作同样成功应用于对抗强化学习和risk-sensitive强化学习领域。

论文链接: https://arxiv.org/pdf/2001.02811.pdf

论文代码:

https://github.com/Jingliang-Duan/Distributional-Soft-Actor-Critic

视频链接:

https://www.bilibili.com/video/BV1fa4y1h7Mo#reply3178996263

RLChina课程slide

【RLChina2020公开课课件】 Lecture-0/1.pdf

【RLChina2020公开课课件】 Lecture-2.pdf

【RLChina2020公开课课件】 Lecture-3.pdf

【RLChina2020公开课课件】 Lecture-4.pdf

【RLChina2020公开课课件】 Lecture-7.pdf

【RLChina2020公开课课件】Lecture-8.pdf