线性代数的直观指南 第二部分

翻译小组成员介绍: 胡智杰    

 谢菲尔德大学 数学与统计学硕士(在读)

英文网址: betterexplained.com/articles/linear-algebra-guide/

可视化矩阵

Visualizing The Matrix

只用语言很难表达清楚。那下面是我将输入、运算和输出可视化的结果:

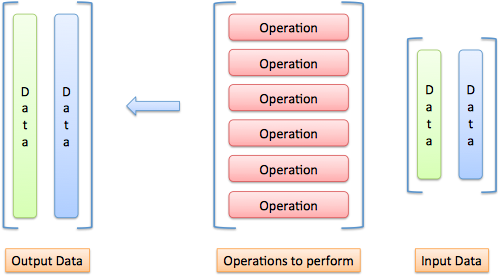
想象一下我们是将每一个 Data 输入“倒入”在每个运算中:

当输入的元素经过一个运算时，它会创建一个输出结果项。在我们的示例中，输入(a、b、c)与操作 F 相反，输出3a + 4b + 5c。它与操作 G 相反，输出 3a + 0 + 0。

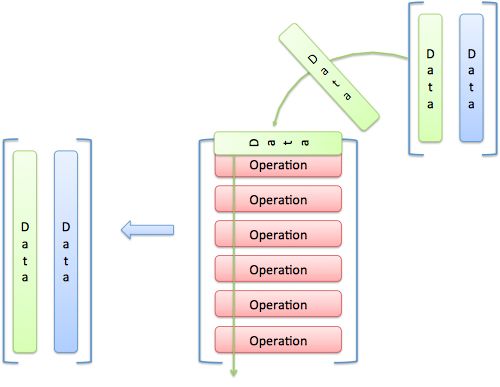
接下来到了红色部分。下面的矩阵是我们图表的简写:

矩阵A是表示输入或运算电子表格的一个单一变量。

棘手之处之一: 阅读的顺序

我们使用功能符号, 像y = f(x)和f(x)= y，而不是按照输入=> 矩阵=>输出流的顺序。我们通常以一个矩阵以大写字母(F), 和一个单个的包含小写(x)的输入列。因为我们有几个输入值(A)和输出值(B), 如下所示的矩阵表示形式:

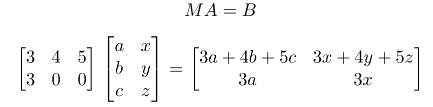
棘手之处之二: 编号

矩阵大小用 R × C 表示: 行计数，列计数，缩写为“m × n”(我听说，“r × c”更容易记住)。矩阵中的项目以同样的方式引用: aij是第i行和第j列(我听说，“i”和“j”在黑板上很容易混淆)。

为什么RC的排序有意义? 我们的运算矩阵是2行3列的，输入矩阵是3行2列。把他们写在一起就是下面形式:

注意，矩阵在“运算值”和“输入值”处接触(n = p)，它们应该匹配! 实际上，我们只有在n = p的情况下才能对矩阵进行乘法运算。

输出矩阵对于每个输入有m个运算行，那么q个输入值，就会得出一个“m x q”矩阵。

更漂亮的运算

Fancier Operations

让我们熟悉运算。假设有3个输入，我们可以得到几个1-运算矩阵:

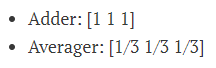
 “Adder”就是a + b + c，“Averager”也是同样的意思: (a + b + c)/3 = a/3 + b/3 + c/3。试试这些1-liners:

• First-input       only: [1 0 0]

• Second-input   only: [0 1 0]

• Third-input      only: [0 0 1]

如果我们把它们合并成一个矩阵

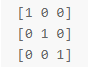
哇哦，这是“单位矩阵”，它将3个输入复制到3个输出，结果不变。

那下面这矩阵呢？

只不过重新排列了输入值的顺序: (x, y, z)变成了(x, z, y)

然后这个呢？

它是输入倍增器。我们可以把它改写成 2*I(单位矩阵)。

是的，当我们决定把输入当作向量坐标时，运算矩阵会变换我们的向量。请看这里《图解线性代数》系列文章:

倍率:使所有输入变得更大/更小

倾斜:使某些输入变大/变小

翻转:使输入为负

旋转:在旧坐标的基础上做新坐标(东变北，北变西等)

这些是乘法的几何解释，以及如何扭曲向量空间。这里只需要记住向量是要修改的数据的例子。

一个非矢量的例子: 股票市场投资组合

A Non-Vector Example: Stock Market Portfolios

让我们在现实世界中应用线性代数:

• 输入数据: 以美元计价的苹果、谷歌和微软股票的股票组合

• 运算: 新闻事件后公司股票价格的变化

• 输出: 更新投资组合

另外还有奖金产出: 让我们做一个新的投资组合，列出这次活动的净利润/亏损。

通常，我们会在电子表格中跟踪它。让我们学着用线性代数思考:

• 输入向量可以是($Apple， $Google，$Microsoft)，显示每种股票的美元。(哦!这些美元价值可以来自另一个矩阵，这个矩阵是股票数量乘以价格。太奇妙了!)

• 4个输出运算应该是: 更新后的苹果市值，更新后谷歌市值，更新后微软市值，计算利润.

将问题可视化。想象在每个运算中运行:

 

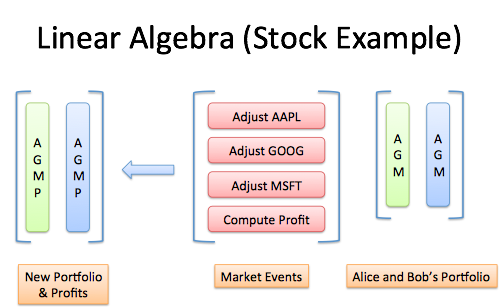
关键是理解为什么我们要像这样建立矩阵，而不是盲目地计算这些数字。

明白了吗?让我们介绍一下场景。

假设一个秘密的设备发布了: 苹果股价上涨20%，谷歌下跌5%，而微软保持不变。我们想调整每个股票价值，使用类似单位矩阵的东西:

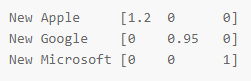
新的苹果市值是原来的，增加了20%(谷歌= 5%下降，微软=不变)。

哦,等一下!我们需要整体利润:

总变化=（0.20 *苹果)+ (-0.05 *谷歌)+ (0 * Microsoft)

我们的最终操作矩阵:

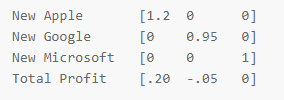
理解吗?输入三次，输出四次。前三个操作是“调整计算后的副本”，最后一个操作将更改组合在一起。

现在让我们输入Alice($1000， $1000， $1000)和Bob($500， $2000， $500)的投资组合。我们可以手工处理这些数字，或者使用Wolfram Alpha(计算):

(注意:输入应该在列中，但是更容易键入行。由 τ (tau)表示的转置运算将行转换为列。)

最后的数字:爱丽丝拥有1200美元的苹果(AAPL)， 950美元的谷歌(GOOG)， 1000美元的微软(MSFT)，净利润150美元。鲍勃拥有600美元的苹果(apple)、1900美元的歌(1900美元)和500美元的微软(MSFT)，净利润为0美元。

发生什么事情了?我们用自己的"电子表格"计算数学。线性代数在19世纪出现，电子表格在20世纪80年代发明。我把这一差距归咎于线性代数教育的落后。(未完待续)