谷歌NIPS'21 | 如何让图神经网络更稳健？

点击上方 蓝字关注我们

【导读】图神经网络（GNN）是机器学习的强大工具之一，但在训练数据上往往依赖于特定领域，为了解决由领域转移和数据标记偏差造成的性能下降，谷歌提出了一种新方法。

图神经网络（GNN），是在机器学习中利用图形结构数据的强大工具。图是一种灵活的数据结构，可以对许多不同类型的关系进行建模，并已被用于不同的应用，如交通预测、谣言和假新闻检测、疾病传播建模等。

作为机器学习的标准之一，GNN假设训练样本是均匀随机选择的（即独立和相同分布样本）。这个假设对于标准的学术数据集来说是很容易符合的，这些数据集专门为研究分析而创建，每个数据节点都已经被标记。

但是在许多现实世界的场景中，数据是没有标签的，实际上，对数据的标记往往是一个繁重的过程，需要熟练的真人审核和把关，所以，要标记所有数据节点是一个非常困难的任务。

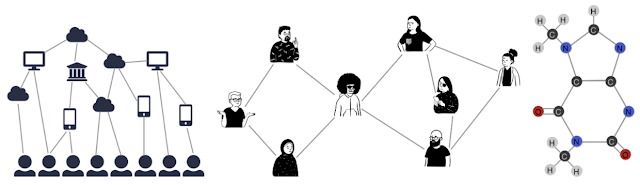
此外，训练数据的偏见也是一个常见问题，因为选择节点进行数据标记的行为通常不是上文所说的「均匀随机选择」。

比如，有时会使用固定的启发式方法来选择一个数据子集（子集中的数据具备一些共同的特征）进行标注，还有的时候，人类分析员会利用复杂的领域知识，单独选择某些特定数据项进行标注。

为了量化训练集中存在的偏差量，我们可以使用一些方法来衡量两个不同的概率分布之间的转变有多大，转变的大小可以被认为是偏差量。

这种偏差量越大，机器学习模型从存在偏见的训练集中归纳出特征的难度就越大。可能会有显著损害模型泛化能力。在学术数据集中，一些领域转移会导致模型性能下降15-20%（以F1分数为量度）。

论文链接：https://proceedings.neurips.cc/paper/2021/file/eb55e369affa90f77dd7dc9e2cd33b16-Paper.pdf

为了解决这个问题，谷歌在NeurIPS 2021上介绍了一种在有偏见的数据上使用GNN的解决方案。

这种方法被称为Shift-Robust GNN（SR-GNN），从名字上不难看出，这个方法的目的就是要让问题域发生变化和迁移时，模型依然保持高稳健性，降低性能下降。

研究人员在半监督学习的常见GNN基准数据集上，用有偏见的训练数据集进行的各种实验中，验证了SR-GNN的有效性，实验表明，SR-GNN在准确性上优于其他GNN基准，将有偏见的训练数据的负面影响减少了30-40%。

数据分布偏移对GNN性能的影响

为了证明数据分布的偏移如何影响GNN的性能，首先为已知的学术数据集生成一些有偏见的训练集。然后，为了理解这种影响，将泛化（测试准确率）与分布偏移的衡量标准（CMD）进行对比。

例如，以著名的PubMed引文数据集为例，它可以被认为是一个图，图的节点就是医学研究论文，图的「边」就是这些论文之间的引用。如果为PubMed生成有偏见的训练数据，这个图看起来像下面这样。

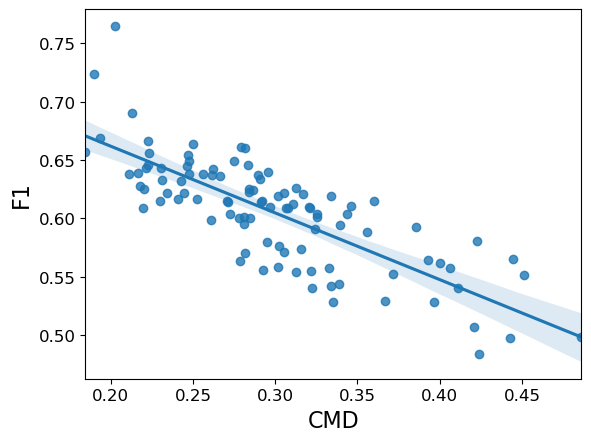
可以看到，数据集的分布偏移与分类准确率之间存在着强烈的负相关：随着CMD的增加，性能（F1）显著下降。也就是说，GNN可能难以泛化，因为训练数据看起来不太像测试数据集。

为了解决这个问题，研究人员提出了一个对泛化高稳健性的正则化器，让训练数据和来自未标记数据的随机均匀样本之间的分布偏移实现最小化。

为了实现这一点，研究人员在模型训练时对域偏移进行实时测量，并在此基础上使用直接惩罚策略，迫使模型尽可能多地忽略训练偏差，让模型为训练数据学习的特征编码器对任何可能来自不同分布的未标记数据也能有效工作。

下图所示为SR-GNN与传统GNN模型的对比。二者输入相同，层数相同。将GNN的第（k）层的最终嵌入Zk与来自未标记的数据点的嵌入进行比较，验证该模型是否正确编码。

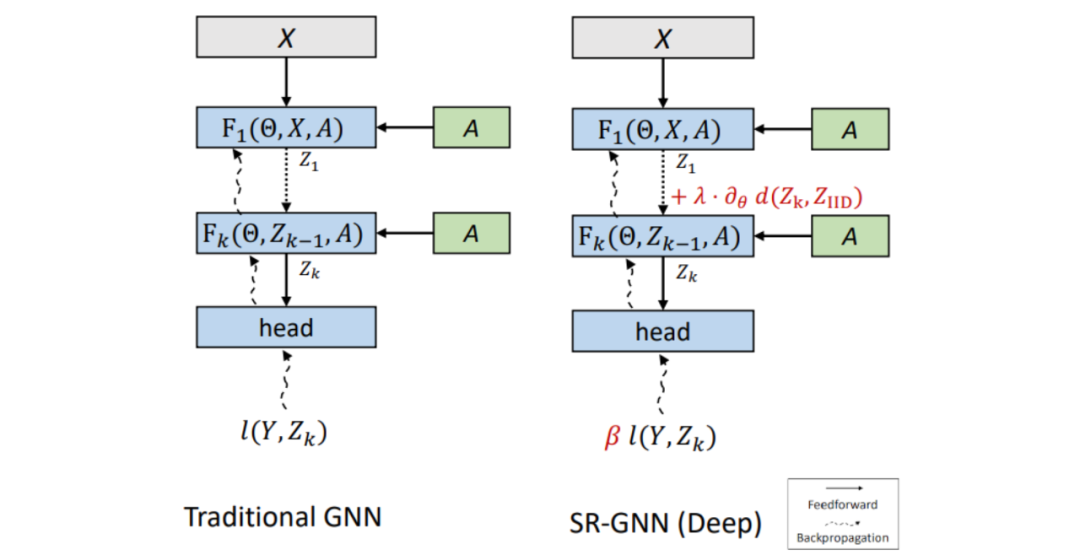
把这个正则化写成模型损失公式中的一个附加项，该公式基于训练数据的表征和真实数据的分布之间的距离制定。

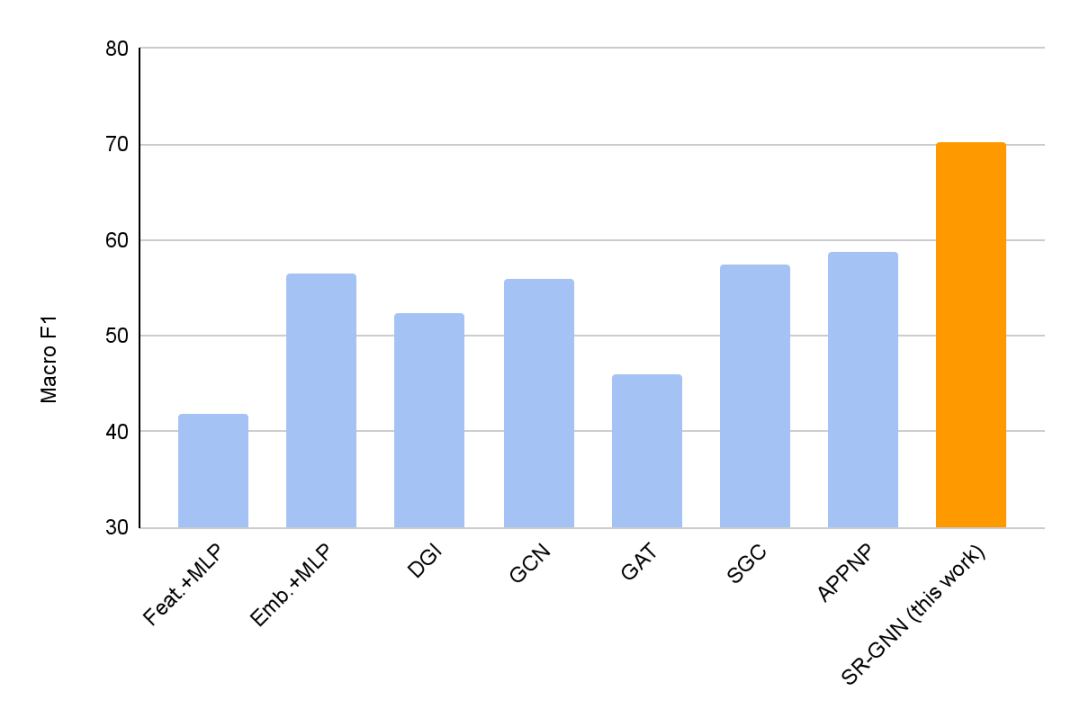
实验证明，加入SR-GNN正则化后，在有偏见的训练数据标签的分类任务上，分类模型的性能实现了30-40%的提升。

另外，本文还研究了如何在有偏见的训练数据存在的情况下，让模型更加可靠。

尽管由于结构差异，相同的正则化机制不能直接应用在不同模型上，但可以通过根据训练实例与近似的真实分布的距离重新加权来「纠正」训练偏见。这能够纠正有偏见的训练数据的分布，无需通过模型来传递梯度。

这两种正则化可以结合，形成一个广义的损失正则化，结合了领域正则化和实例重权（细节，包括损失公式，可在论文中找到）。

结论

有偏见的训练数据在现实世界的场景中很常见，这些偏见可能是由于各种原因造成的，包括对大量数据进行标注的困难、用于选择标注节点的各种启发式方法或不一致的技术、数据标记分布延时等等。

这个通用框架（SR-GNN）可以减少有偏见的训练数据的影响，而且可以应用于各种类型的GNN，包括更深层的GNN，以及这些模型的线性化浅层GNN上。

参考资料：

https://proceedings.neurips.cc/paper/2021/file/eb55e369affa90f77dd7dc9e2cd33b16-Paper.pdf

https://ai.googleblog.com/2022/03/robust-graph-neural-networks.html?m=1