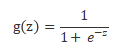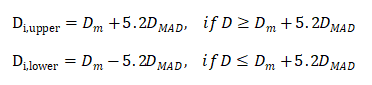机器学习初探：Logistic选股模型实证

本文为量子金服原创文章，转载须授权

往期回顾：

上帝手中的骰子——无所不能的贝叶斯（上篇）

上帝手中的骰子——无所不能的贝叶斯（下篇）

机器学习（Machine Learning, ML）是时下最热门的话题之一，应用范围十分广泛。其中，对分类问题的解决，是机器学习的一个常用领域。不难想到，对于选股策略来说，其本质就是一个分类问题，即将股票分成持有和不持有两类。那么，应用机器学习的技术技术进行选股，应当是一个可以尝试的方向。本文中，我们将结合国信证券发布于2010年9月7日的研究报告《Logistic选股模型及其在沪深300中的实证》中的思路，将选股问题转化为一个二元分类问题，从而利用Logistic算法进行预测分类，完成选股。

概念简介

Logistic回归（Logistic Regression，以下简称LR）属于常用的机器学习算法之一，可以用来回归，也可以用来分类，主要用来处理二分类的问题。与传统的二分类方法（例如SVM）不同的是，LR并不是将两个不同类别的样本完全分开，非此即彼，而是返回一个概率值，即预测样本有百分之多少的概率属于正类，又有百分之多少的概率属于负类，这接近于“模糊”（fuzzy）分类的范畴。在实际应用中，LR常被用于估计某种事物的可能性。例如，它可以用于广告预测，也就是根据某广告被用户点击的可能性，把最可能被用户点击的广告摆在用户能看到的地方。还有类似的某用户购买某商品的可能性，某病人患有某种疾病的可能性等等。

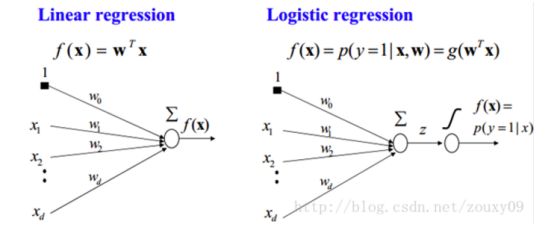
LR的本就是一个线性分类模型，它与线性回归的不同点在于：试图将线性回归输出的很大范围的数，例如从负无穷到正无穷，压缩到0和1之间，用以表达“可能性”。而实现这个功能就需要一个映射，也就是给输出加一个logistic函数（或称sigmoid函数）： 

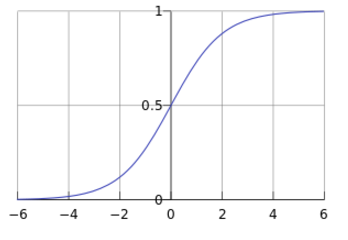
Sigmoid 函数在有个很漂亮的“S”形，如下图所示（引自维基百科）：

也就是说，LR其实本质上是一个被logistic方程归一化后的线性回归过程。

在使用LR模型时，我们首先需要输入一组拥有不同特征（feature）的训练数据，并对每个训练数据事先判断其类别（target）。将这样一组数据输入后，模型将会通过算法“训练”自己，拟合出数据中feature与target之间的联系。完成训练后，我们就可以输入一个预测样本，模型将通过拟合出的关系，判断该样本的feature应当对应于哪一个target，并返回分属于不同target的概率。这就完成了一次完整的LR分类。

策略思路

将选股问题转化为分类问题，预期表现优于大盘的分为正类，低于大盘的分为负类，使用LR模型计算每支股票属于正类的概率。选出属于正类的概率最高的30支股票购入，平均分配资金，每月调仓。

策略细节

1） 分类（target）

我们采用沪深300指数作为基准，研究其中个股收益超越该指数收益率的概率。以每个月为观察周期，当某支股票在整个周期内的收益率超过沪深300指数，我们就将它的target记为1（正类），否则为0（负类）；

2） 特征（feature）

Feature是用来表达数据不同维度特征的量，在股票市场里，因子无疑是作为数据特征的最合适的变量。这里我们参考了东方证券发布于2015年6月26日的研究报告《单因子有效性检验》，选择了十个研报中检验为与收益率相关性最强的因子，用来刻画每一个数据（每一支股票）的不同维度的特征。因子列表如下：

因子名	简称
总市值	TMV
流通市值	FMV
22日涨跌幅	STOCKZF22
均线偏离度	STOCKPJCJ5/60
22日换手率	HSL22
营业收入同比增速（单季）	SALESGROWRATE1
净资产/总市值	BP
净利润同比增速（单季）	PROFITGROWRATE1
营业收入/总市值	SP
营业收入同比增速TTM	SALESGROWRATE

 

3） 极值与标准化处理

使用LR算法对数据质量有一定要求，我们首先要做的工作是数据处理。

a) 极值。极值是指偏离大部分样本群体的值，少数极值的存在就可能极大的扭曲数据分析的结果，因此去极值是必要的。这里我们采用中位数去极值法，公式表达如下：

其中Di表示第i个观察值，Dm表示每一个特征变量的中位数。Dmad为每一个观察值与中位数的偏离量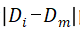的中位数。

b) 标准化

在使用不同因子数据时，必须将其标准化（即映射到[0,1]区间内），否则所有组合将毫无意义，因为每一个因子的单位都是不同的。这里的标准化方式为：

 

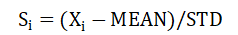
即以0位均值，1位标准差的正态标准化。

策略实现

1） Logistic选股

交易标的：股票

调仓周期：每月

回测时间：2012.01.01~2017.01.01

回测时长：5年

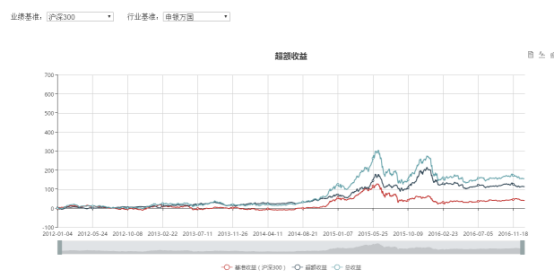
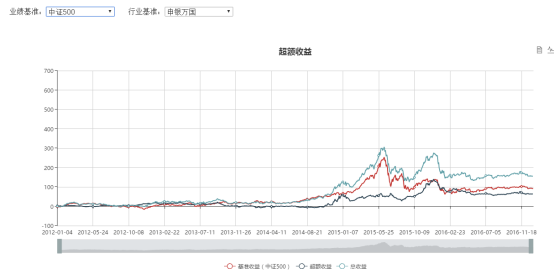
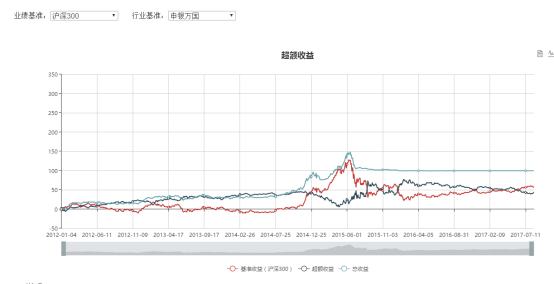
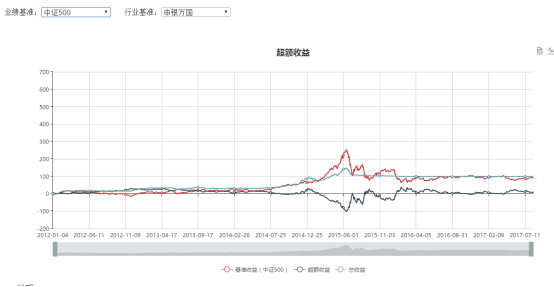
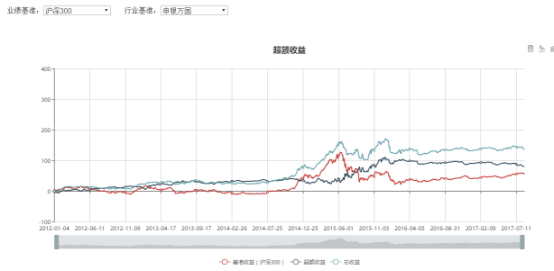
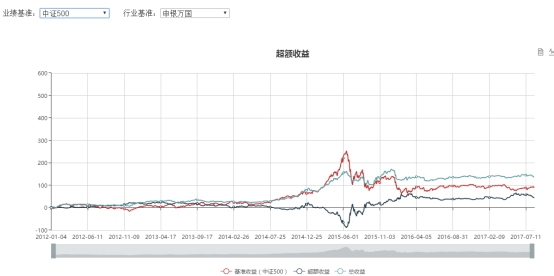
收益曲线 

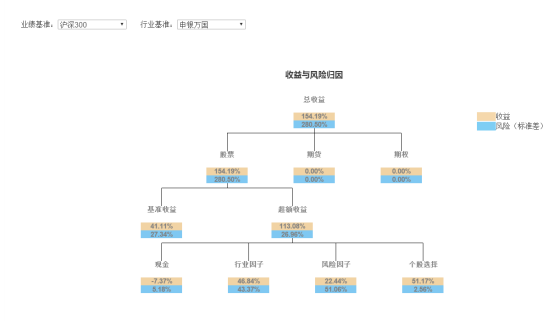
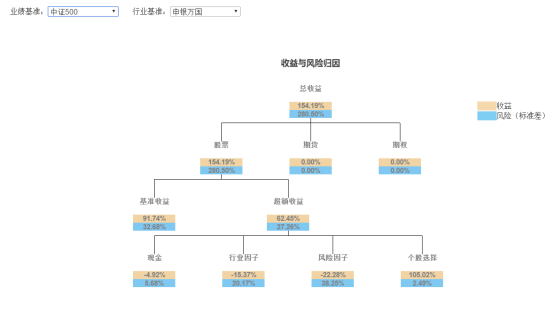
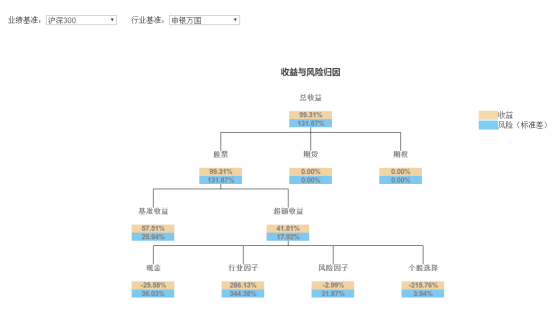
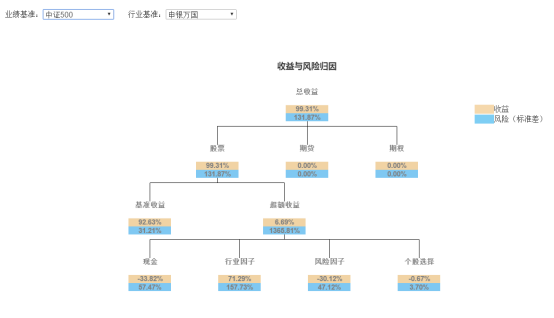
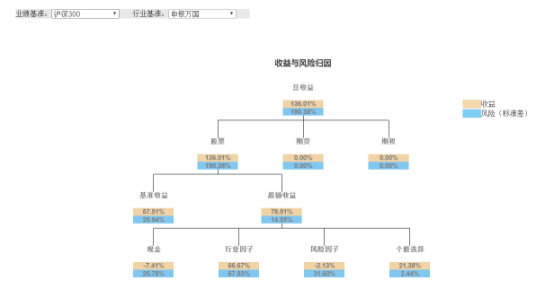
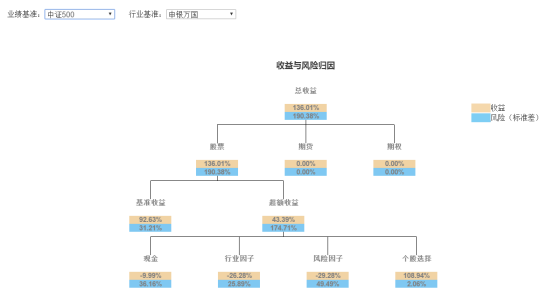
收益归因

业绩分析

回测显示，在五年的回测期内，我们的策略表现良好，取得了31.8%的年化收益率，跑赢沪深300与中证500两个指数。但是也存在回测过大，波动率过高的问题。下面我们将加入回撤控制进行检验。

2） Logistic选股，全时间段回撤控制

交易标的：股票

调仓周期：每月

回测时间：2012.01.01~2017.01.01

回测时长：5年

回撤控制：20%

收益曲线

收益归因

业绩分析

加入全时段的回撤控制后，相较于策略（1），收益率伴随回撤、波动率大幅下滑，夏普率上升，策略表现更加稳健。不过值得注意的是，在2015年下半年的熊市中，投资组合的持仓量降为0，即彻底退出股市，虽然这一定程度上躲开了股市大跌可能带来的损失，但也放弃了之后的潜在收益。为了避免这种情况，我们将回撤控制更改为月度，即控制每月回撤不超过一定阈值。

 

3） Logistic选股，月度回撤控制

交易标的：股票

调仓周期：每月

回撤控制：每月最高20%

回测时间：2012.01.01~2017.01.01

回测时长：5年

收益曲线

收益归因

 

业绩分析

相比于策略（2），策略（3）的收益率、回撤率、波动率都有所上升，夏普率略优于策略（2），相差不大。二者最大的差别在于，策略（3）采用每月控制回撤，每个月都是一个新的开始，在股灾平仓后，下个月仍将参与投资，仍然是资本市场的参与者。而策略（2）在平仓后不再开仓。使用哪种控制方式，应当取决于对策略的信心以及对市场大势的判断。

小结

LR是用机器学习技术处理分类问题的经典方法，将其应用在选股策略上是一个有趣的尝试。从回测结果上看，LR选股策略是行之有效的。值得注意的是，虽然LR模型在机器学习的方法中属于比较简单也比较成熟的模型，但是仍然有很多不同的参数可以设置、调整，本文未多做探索，直接使用了默认设置。此外，因子的选取对模型的预测效果至关重要，在挑选因子的过程中，除了关注因子与收益直接的相关性之外，还应该考量因子彼此直接的相关性，选取本身相关性较低的因子组合，有利于提升模型的稳定性。最后，LR模型只是给出了因子组合与跑赢大盘之间的定量关系，而这样的关系其背后的逻辑是很难合理的解释的，也因此可能无法保证未来选股结果的可靠性与稳定性。

相关课程推荐

三个月教你从零入门人工智能！！| 深度学习精华实践课程：

点击“阅读原文”开启新姿势