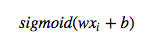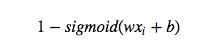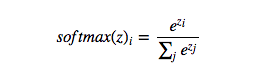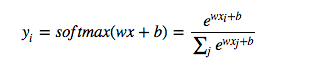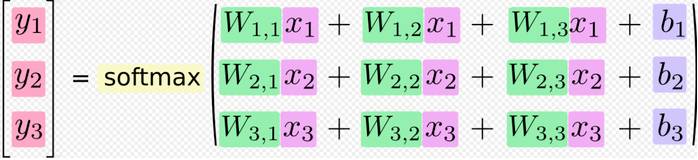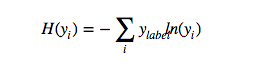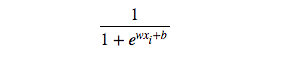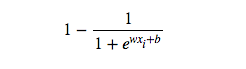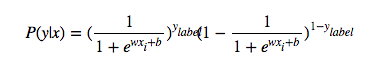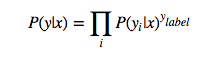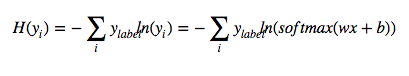10分钟搞懂Tensorflow 逻辑回归实现手写识别

“全球人工智能”拥有十多万AI产业用户，10000多名AI技术专家。主要来自：北大，清华，中科院，麻省理工，卡内基梅隆，斯坦福，哈佛，牛津，剑桥...以及谷歌，腾讯，百度，脸谱，微软，阿里，海康威视，英伟达......等全球名校和名企。

---

——免费加入AI技术专家社群>>

——免费加入AI高管投资者群>>

——申请成为AI高校推广大使>>

1.1. 逻辑回归原理

1.1.1. 逻辑回归

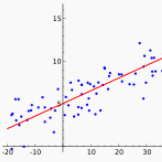
在现实生活中，我们遇到的数据大多数都是非线性的，因此我们不能用上一章线性回归的方法来进行数据拟合。但是我们仍然可以从线性模型着手开始第一步，首先对输入的数据进行加权求和。

线性模型：z=wx+b z = w x + b

其中w我们称为“权重”，b为偏置量（bias）， x x 为输入的样本数据，三者均为向量的形式。

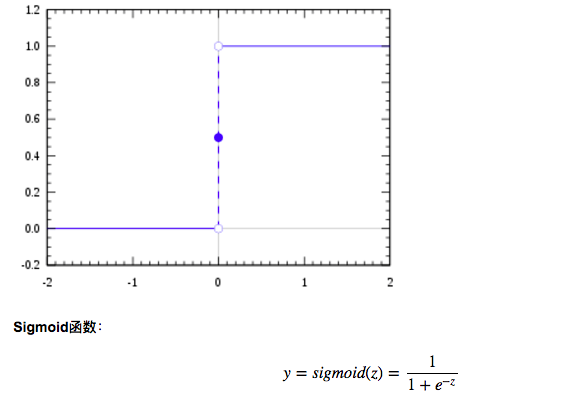
我们先在二分类中来讨论，假如能创建一个模型，如果系统输出1，我们认为是第一类，如果系统输出0，我们认为是第二类，这种输出需求有点像阶跃函数（海维塞德阶跃函数），但是阶跃函数是间断函数，y的取值在x=0处突然跳跃到1，在实际的建模中，我们很难在模型中处理这种情况，所以我们使用Sigmoid函数来代替阶跃函数。

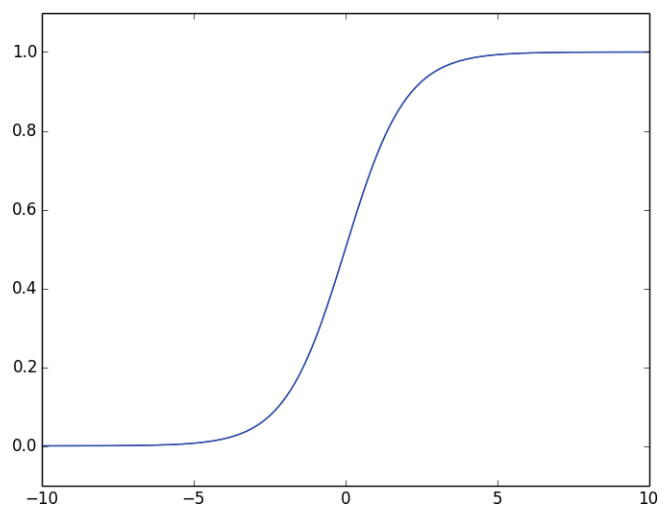
Sigmoid函数是激活函数其中的一种，当x=0时，函数值为0.5，随着x的增大，对应的Sigmoid值趋近1，而随着x的减小，Sigmoid值趋近0。通过这个函数，我们可以得到一系列0—1之间的数值，接着我们就可以把大于0.5的数据分为1类，把小于0.5的数据分为0类。

这种方式等价于是一种概率估计，我们把y看作服从伯努利分布，在给定x条件下，求解每个 y i 为1或0的概率。此时，逻辑回归这个抽象的名词，在这里我们把它转化成了能够让人容易理解的概率问题。接着通过最大对数似然函数估计w值，就解决问题了。
y i 等于1的概率为：

y i 等于0的概率为：

以上对Sigmoid函数描述可以看出该函数多用于二分类，而我们会经常遇到多分类问题，这时，Softmax函数的就派上用场了。

Softmax函数：
Softmax函数也是激活函数的一种，主要用于多分类，把输入的线性模型当成幂指数求值，最后把输出值归一化为概率，通过概率来把对象分类，而每个对象之间是不相关的，所有的对象的概率之和为1。对于Softmax函数，如果j=2的话，Softmax和Sigmoid是一样的，同样解决的是二分类问题，这时用两种函数都能进行很好的二分类。

以上公式可以理解为，样本为类别 i i 的概率。即：

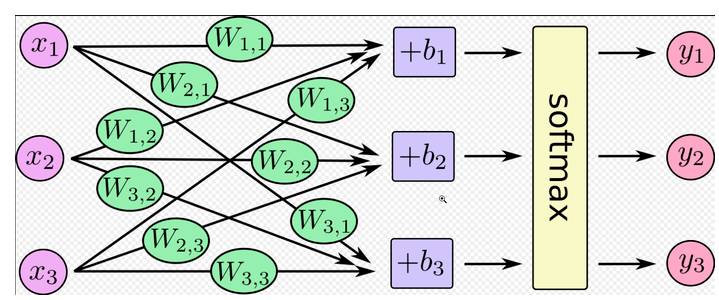
对于Softmax回归模型的解释，在这里引用一下别人的图，一张图片就胜过千言万语。

如果写成多项式，可以是这样：

如果换成我们常用的矩阵的形式，可以是这样：

1.1.2. 损失函数

在线性回归中，我们定义了一个由和方差组成的损失函数，并使该函数最小化来找到 θ 的最优解。同样的，在逻辑回归中我们也需要定义一个函数，通过最小化这个函数来解得我们的权重w值和偏差b值。在机器学习中，这种函数可以看做是表示一个模型的好坏的指标，这种指标可以叫做成本函数（Cost）或损失函数（Loss），然后最小化这两种函数，这两种方式都是一样的。

这里介绍一个常见的损失函数——“交叉熵”，在后面的实例代码中我们会用到。交叉熵产生于信息论里面的信息压缩编码技术，后来慢慢演变成从博弈论到机器学习等其他领域的重要技术，它用来衡量我们的预测用于描述真相的低效性。它的定义如下：

它是怎么推导出来的呢，我们先来讨论一下Sigmoid的损失函数，接着再来对比理解。在上面的二分类中问题中，我们使用Sigmoid函数，同时我们也假定预测值 y i 服从伯努利分布，则 y i 等于1的概率为：

y i 等于0的概率为：

则概率密度函数为：

上式中的 y l a b e l 是样本为类别1的实际概率。接着我们取对数似然函数，然后最小化似然函数进行参数估计（这里省略似然函数和一系列文字）。
而我们把问题泛化为多分类时，同样可以得出我们的概率密度函数：

我们对概率密度取自然对数的负数，就得到了我们的似然函数，即我们这里称为交叉熵的函数，其中 y i 是样本为类别 i 的预测概率m y l a b e l 是样本为类别 i 的实际概率。

最后，通过最小化该交叉熵，找出最优的w和b值。

1.2. 实例：手写识别系统

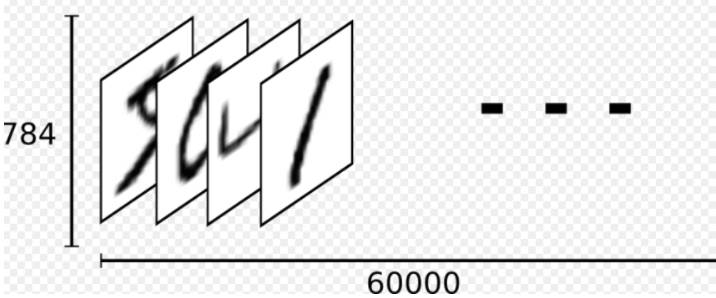
了解了逻辑回归的工作原理以后，现在我们用tensorflow来实现一个手写识别系统。首先我们必须去挖掘一些数据，我们使用现成的MNIST数据集，它是机器学习入门级的数据集，它包含各种手写数字图片和每张图片对应的标签，即图片对应的数字（0~9）。你可以通过一段代码把它下载下来，在下载之前记得安装python-mnist：

下载下来的数据总共有60000行的训练数据集(mnist.train)，和10000行的测试数据集(mnist.test)，同时我们把图片设为x，x是一个shape=[None，784]的一个张量，None表示任意长度，比如它可以小于或等于mnist.train里面的60000张图片。另外，每一张图片包含28像素X28像素，向量长度为28*28=789，表示图片是由784维向量空间的点组成的。然后，我们把图片的标签设为y_张量,shape=[None,10]，这个y_的值就是图片原本对应的标签（0~9的数字）。

用代码来表示可以参考：

数据都准备好以后，就开始训练我们的模型了。之前我们讲了Softmax函数，用该函数来做逻辑回归，我们可以通过这样的代码来表示：

cross_entropy = -tf.reduce_sum(y_ * tf.log(y))

但是Tensorflow已经实现好了这个Softmax函数，即：tf.nn.softmax_cross_entropy_with_logits()，而无需我们自己这样定义（-tf.reduce_sum(y_ * tf.log(y))）。为什么使用Tensorflow的呢，是因为我们在使用该函数的时候，可能会出现数值不稳定的问题，需要自己在Softmax函数中加一些trick，这样做起来比较麻烦，又把模型复杂化了，所以我们推荐使用Tensorflow自带的交叉熵函数，它会帮你处理数值不稳定的问题。

-tf.reduce_sum(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))

逻辑回归确定好各项函数后，我们还是用梯度下降的方式去寻找那个最优的w和b值，最后，整个手写图片识别系统的代码如下：

import numpy as npimport tensorflow as tffrom tensorflow.examples.tutorials.mnist import input_datamnist = input_data.read_data_sets("MNIST_data/", one_hot=True)from mnist import MNISTmndata = MNIST('MNIST_data')sess = tf.Session()x = tf.placeholder("float", [None, 784])W = tf.Variable(tf.zeros([784, 10]))b = tf.Variable(tf.zeros([10]))y = tf.matmul(x, W) + by_ = tf.placeholder("float", [None, 10])# 使用Tensorflow自带的交叉熵函数cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y)train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)init = tf.global_variables_initializer()sess.run(init)for i in range(1000):   batch_xs, batch_ys = mnist.train.next_batch(500)   sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})images, labels = mndata.load_testing()num = 9000image = images[num]label = labels[num]# 打印图片print(mndata.display(image))print('这张图片的实际数字是: ' + str(label))# 测试新图片，并输出预测值a = np.array(image).reshape(1, 784)y = tf.nn.softmax(y)  # 为了打印出预测值，我们这里增加一步通过softmax函数处理后来输出一个向量result = sess.run(y, feed_dict={x: a})  # result是一个向量，通过索引来判断图片数字print('预测值为：')print(result)--result...........................................................................................................................................................@@@......................@@@@@@@....................@@@....@@..................@@......@@.........................@@.........................@@@.......................@@@@......................@@@@@@.....................@@@@.@@@...........................@@..........................@@...........................@@..........................@@.........................@@...............@..........@@...............@.........@@................@........@@@................@@.....@@@...................@@@@@@@.......................@.....................................................................................................这张图片的实际数字是: 3预测值为：[[ 0.  0.  0.  1.  0.  0.  0.  0.  0.  0.]]

读者可以通过改变不同的图片来试试预测的结果，可以看出上面的预测情况还是很不错的。但是我们模型的性能到底如何，还是需要数据来说话，测试性能的代码如下：

# 检测预测和真实标签的匹配程度correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))# 转换布尔值为浮点数，并取平均accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))# 计算模型在测试数据集上的正确率 print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))--result0.9022

这个结果真的不怎么样，不过我们可以通过采用其他算法和模型来改进我们的性能，但这已超过了本节要讲的范围，我们仅需通过本章内容了解逻辑回归的工作原理就好了。以后我们可以共同探讨改进一下，从而进一步提升模型的准确率。

原文：http://www.cnblogs.com/vipyoumay/p/7507149.html

系统学习，进入全球人工智能学院

热门文章推荐

汤晓鸥教授：人工智能让天下没有难吹的牛!

英伟达发布全球首款人工智能全自动驾驶平台

未来 3~5 年内，哪个方向的机器学习人才最紧缺？

中科院步态识别技术：不看脸 50米内在人群中认出你！

厉害｜黄仁勋狂怼CPU:摩尔定律已死 未来属于GPU!

干货｜7步让你从零开始掌握Python机器学习！

华裔女科学家钱璐璐，发明仅20纳米的DNA机器人！

Geoffrey Hinton提出capsule 概念，推翻反向传播！

2017年7大最受欢迎的AI编程语言：Python第一!

重磅｜中国首家人工智能技术学院在京揭牌开学！