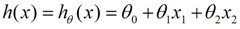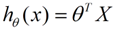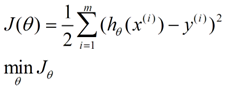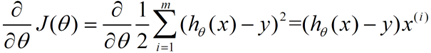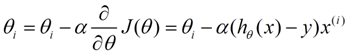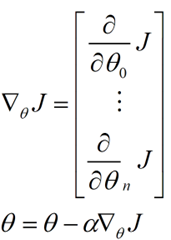今日面试题分享：说说梯度下降法

2019 年 2 月 26 日 七月在线实验室

undefined

今日面试题分享

说说梯度下降法

参考答案：

1 什么是梯度下降法 

经常在机器学习中的优化问题中看到一个算法，即梯度下降法，那到底什么是梯度下降法呢？ 

维基百科给出的定义是梯度下降法（Gradient descent）是一个一阶最优化算法，通常也称为最速下降法。 

要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索，则会接近函数的局部极大值点；这个过程则被称为梯度上升法。

额，问题又来了，什么是梯度？为了避免各种复杂的说辞，咱们可以这样简单理解，在单变量的实值函数的情况，梯度就是导数，或者，对于一个线性函数，也就是线的斜率。 

1.1 梯度下降法示例 
举个形象的例子吧，比如当我们要做一个房屋价值的评估系统，那都有哪些因素决定或影响房屋的价值呢？

比如说面积、房子的大小（几室几厅）、地段、朝向等等，这些影响房屋价值的变量被称为特征(feature)。在这里，为了简单，我们假定房屋只由一个变量影响，那就是房屋的面积。 

假设有一个房屋销售的数据如下： 
面积(m^2)  销售价钱（万元） 
123            250 
150            320 
87              160 
102            220
 …               …
 

插句题外话，顺便吐下槽，这套房屋价格数据在五年前可能还能买到帝都5环左右的房子，但现在只能买到二线城市的房屋了。
 

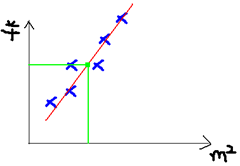
我们可以做出一个图，x轴是房屋的面积。y轴是房屋的售价，如下：


如果来了一个新的房子/面积，假设在房屋销售价格的记录中没有的，我们怎么办呢？ 

我们可以用一条曲线去尽量准的拟合这些数据，然后如果有新的输入面积，我们可以在将曲线上这个点对应的值返回。如果用一条直线去拟合房屋价格数据，可能如下图这个样子：


而图中绿色的点就是我们想要预测的点。
  
而图中绿色的点就是我们想要预测的点。
 

为了数学建模，首先给出一些概念和常用的符号。 

房屋销售记录表 – 训练集(training set)或者训练数据(training data), 是我们流程中的输入数据，一般称为x 

房屋销售价钱 – 输出数据，一般称为y 

拟合的函数（或者称为假设或者模型），一般写做 y = h(x) 

训练数据的条目数(#training set), 一条训练数据是由一对输入数据和输出数据组成的 

输入数据的维度(特征的个数，#features)，n
 

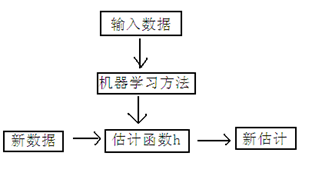
然后便是一个典型的机器学习的过程，首先给出一个输入数据，我们的算法会通过一系列的过程得到一个估计的函数，这个函数有能力对没有见过的新数据给出一个新的估计，也被称为构建一个模型。


我们用X1，X2..Xn 去描述feature里面的分量，比如x1=房间的面积，x2=房间的朝向等等，我们可以做出一个估计函数：


θ在这儿称为参数，在这儿的意思是调整feature中每个分量的影响力，就是到底是房屋的面积更重要还是房屋的地段更重要。

如果我们令X0 = 1，就可以用向量的方式来表示了：


我们程序也需要一个机制去评估我们θ是否比较好，所以说需要对我们做出的h函数进行评估，一般这个进行评估的函数称为损失函数（loss function），描述h函数不好的程度，这里我们称这个函数为J函数。


换言之，我们把对x(i)的估计值与真实值y(i)差的平方和作为损失函数，前面乘上的系数1/2是为了方便求导（且在求导的时候，这个系数会消掉）。

如何调整θ以使得J(θ)取得最小值有很多方法，其中有最小二乘法(min square)，是一种完全是数学描述的方法，另外一种就是梯度下降法。
 


1.2 梯度下降算法流程
 

梯度下降法的算法流程如下：
1）首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。 
2）改变θ的值，使得J(θ)按梯度下降的方向进行减少。

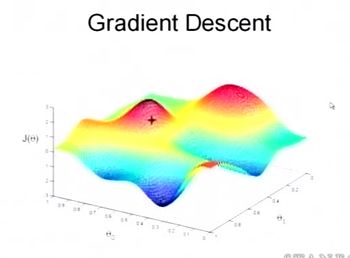
为了描述的更清楚，给出下面的图：


这是一个表示参数θ与误差函数J(θ)的关系图，红色的部分是表示J(θ)有着比较高的取值，我们需要的是，能够让J(θ)的值尽量的低，也就是达到深蓝色的部分（让误差/损失最小嘛）。

θ0，θ1表示θ向量的两个维度。

在上面提到梯度下降法的第一步是给θ给一个初值，假设随机给的初值是在图上的十字点。

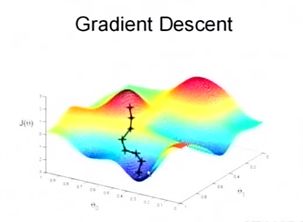
然后我们将θ按照梯度下降的方向进行调整，就会使得J(θ)往更低的方向进行变化，如下图所示，算法的结束将是在θ下降到无法继续下降为止。


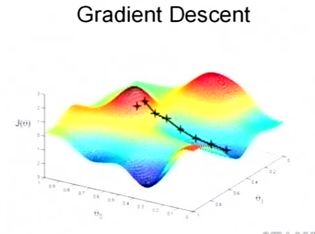
当然，可能梯度下降的最终点并非是全局最小点，即也可能是一个局部最小点，如下图所示：


上面这张图就是描述的一个局部最小点，这是我们重新选择了一个初始点得到的，看来我们这个算法将会在很大的程度上被初始点的选择影响而陷入局部最小点。 

下面我将用一个例子描述一下梯度减少的过程，对于我们的函数J(θ)求偏导J：


下面是更新的过程，也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值，-后面的部分表示按梯度方向减少的量，α表示步长，也就是每次按照梯度减少的方向变化多少。

一个很重要的地方值得注意的是，梯度是有方向的，对于一个向量θ，每一维分量θi都可以求出一个梯度的方向，我们就可以找到一个整体的方向，在变化的时候，我们就朝着下降最多的方向进行变化就可以达到一个最小点，不管它是局部的还是全局的。

用更简单的数学语言进行描述步骤2）是这样的：


本题解析来源：@LeftNotEasy
链接：http://www.cnblogs.com/LeftNotEasy/archive/2010/12/05/mathmatic_in_machine_learning_1_regression_and_gradient_descent.html