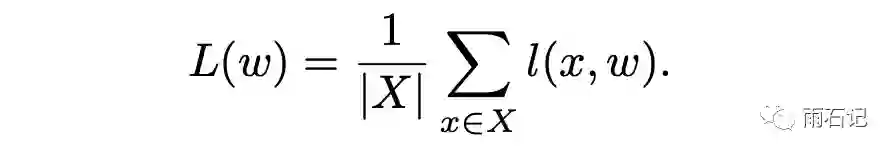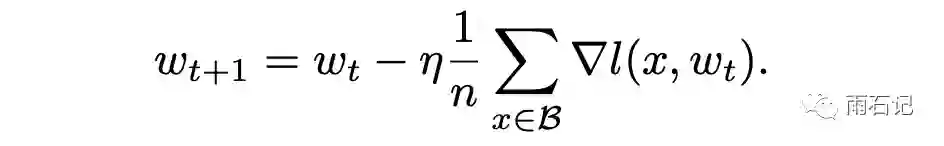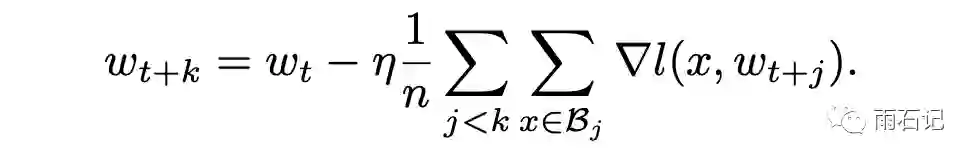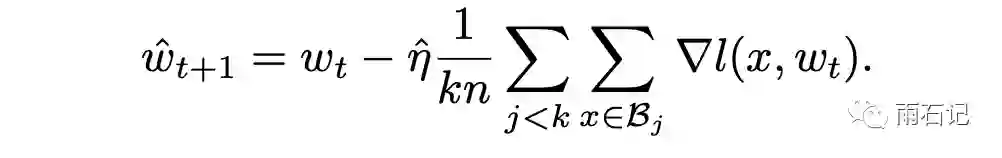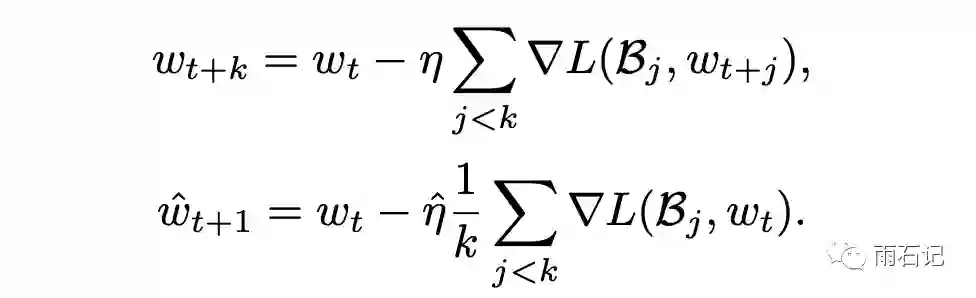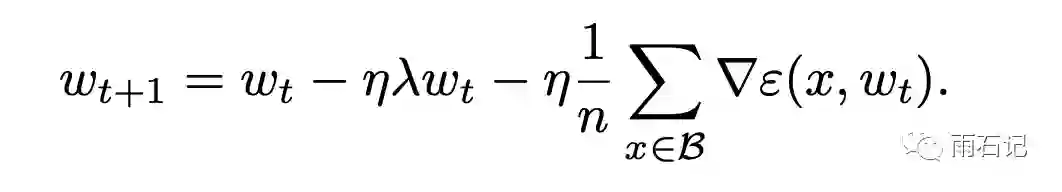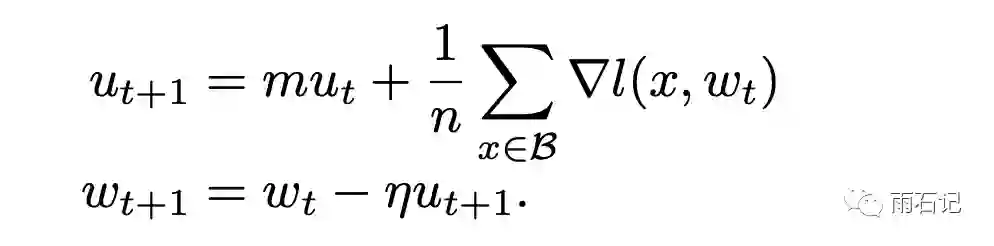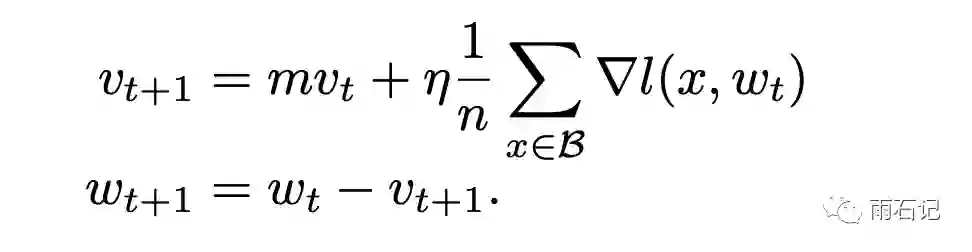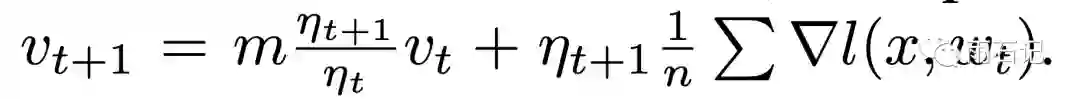会员服务 ·

大批量SGD: 1小时训练ImageNet

2020 年 9 月 28 日 AINLP

在分布式深度学习之参数服务器架构一文，给大家介绍了并行化训练模型的分布式架构。在PS架构中，梯度是同步更新还是异步更新是一个问题，同步更新会有短板效应，即训练速度和最慢的机器持平，而异步训练则有较好的并行提速和正则化效应。

但近两年来，模型训练加速的趋势反倒是采用同步式的大批量的数据训练，这点在Federated Learning: 问题与优化算法就有所体现，里面提到的Federated Averaging算法就是一个大批量的例子。

本文是较早的采用大批量SGD去做训练的论文[1]的阅读笔记，里面提出了很多在大批量训练时候的技巧。

回顾

首先，先来回顾一下mini-batch的梯度下降算法。在全部数据集上的损失函数计算如下:

那么mini-batch的梯度下降计算公式如下:

其中，η是学习率，n为当前mini-batch的样本数，B为mini-batch中的样本集合。

技巧一: 学习率和批数据大小呈线性关系

当把mini-batch的size扩大k倍时，学习率也应该相应的扩大k倍。

其理论基础如下，如果k个mini-batch一步一步进行训练的话，那么得到的梯度更新公式如下：

而如果在一个大的batch中，梯度更新公式如下：

这其中的区别就在于，k步训练中每一步计算梯度的参数状态是变化的，而一步计算相当于k个批次都用的是最初始的参数状态计算梯度。

如果假设每一步的参数状态变化不大的话，那么这样做就是可行的。而只有这样做了，才能使得大batch训练的学习曲线和一步一步训练的曲线是类似的。

当然，上面做的假设是一个强假设，在训练刚开始的时候一般是不成立的，因为此时模型的参数状态变化是很大的，因而，在刚开始的时候，需要使用一些warmup策略。

虽然这种方式可以有效的提升训练速度，但是实验发现，当batch-size超过一定阈值后，会导致效果的退化，实验中是在~8k以内这个技巧都有效。

技巧二: 不同的warmup

论文提出了两种warmup策略：

恒定warmup: 在最开始的5个epoch中使用一个较小的learning_rate，然后再使用k*η作为后面的学习率
渐变warmup: 在最开始的1个epoch使用一个较小的learning rate，然后在5个epoch中逐步将learning rate增加到k*η.

其中，第一个策略因为在第5个epoch的时候会有较大变化，所以会导致loss有个突起的尖峰。所以，一般采用第二种策略。

技巧三: 在本地数据上进行批归一化

批归一化一般是在参与一步训练的所有数据上做。但是让我们再次回顾大批量的初衷，大batch的目的是让k步训练合并为分布式系统上的一步，所以做了每步梯度都相差不大的假设。而k步训练的话，每一步都是在小batch上做的。所以，当把k步训练的数据合并为一步时，批归一化也应该是在大batch的1/k数据上分别做k次。

对应到分布式的训练上，就是保证每个worker上的数据都和原来小batch的batch_size一样，然后批归一化就在小batch上直接做。

这样也省掉了为批归一化计算全局统计值的通信开销。

陷阱一: 权重衰减

不同的平台的实现方式不同，所以论文还介绍了几种不容易被发现的实现上的问题，第一个问题就是权重衰减。

在计算损失函数的时候，一般我们会加正则化项:

加了正则化项之后，梯度的计算变成:

这样，梯度更新时就多了一个ηλw_t项，因为是线性的，所以很多平台的实现中都是单独去对它进行计算的。因而就造成了一个陷阱，即:

将交叉熵损失增大k倍并不是正确的增大学习率的方法，因为还有一个分项上的学习率没有扩大。

陷阱二: 冲量校正

一般情况下，为了加快训练，往往使用SGD + momentum算法。

而这个算法在很多平台的实现中往往有个变种:

在η不变的情况下，这两种方法是等价的，但如果η变化，那么如果使用后一种，就需要用如下方法校正:

陷阱三: 梯度聚合

在分布式系统中，聚合操作往往是加法而非平均，因而，一般在worker需要提前除以k然后聚合的时候直接加起来就可以。

实验结果

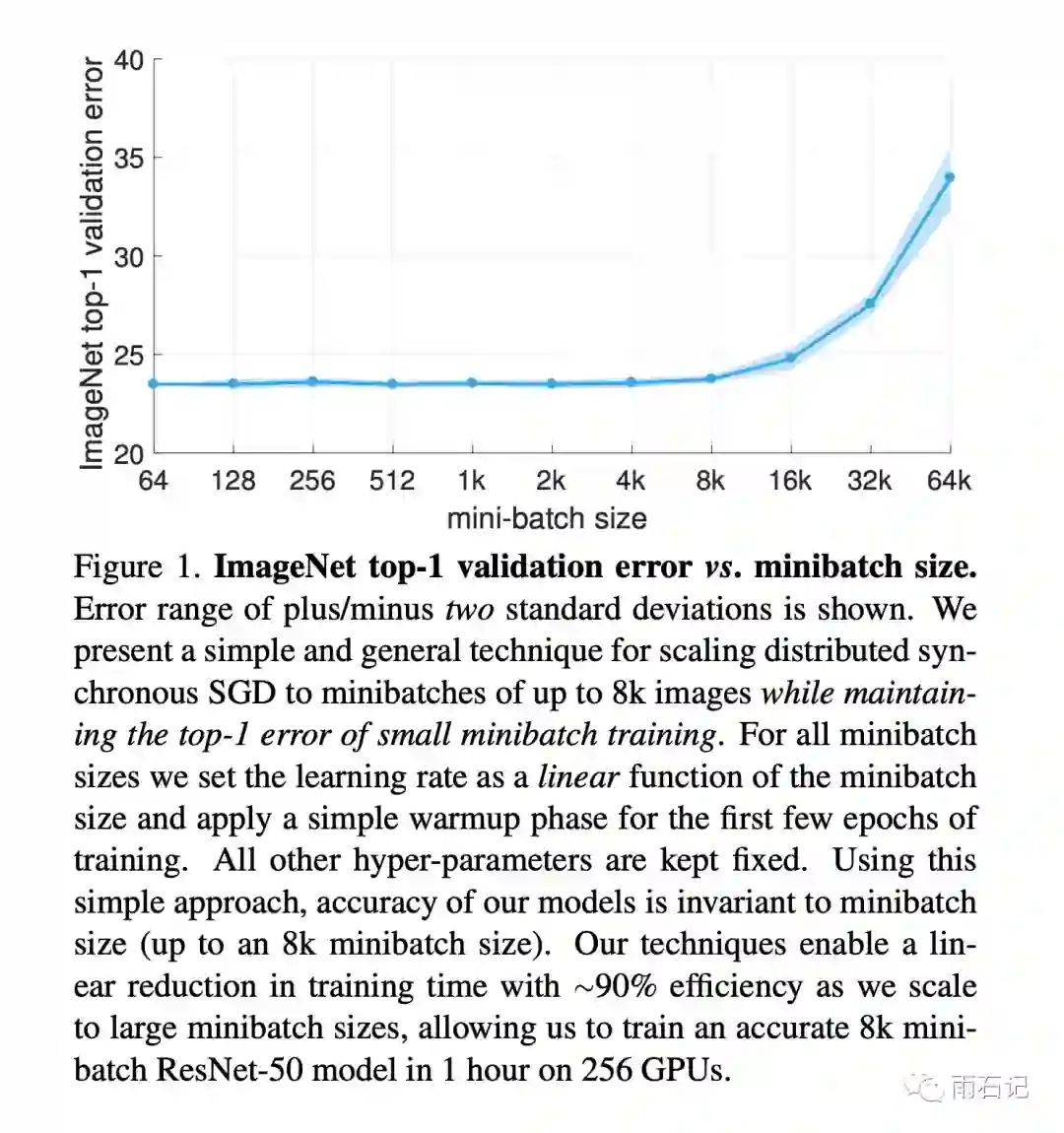
使用256个GPU进行训练的话，可以在1小时内将ResNet-50模型训练好。模型效果和batch_size的关系如下，可以看到，在batch_size超过8k的时候，效果有明显的drop。

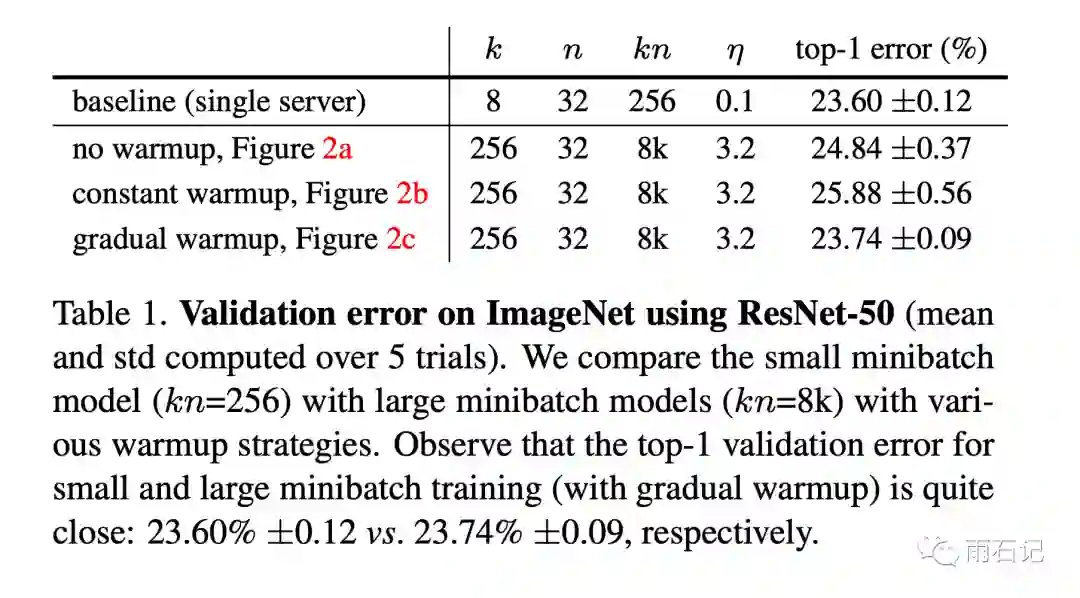
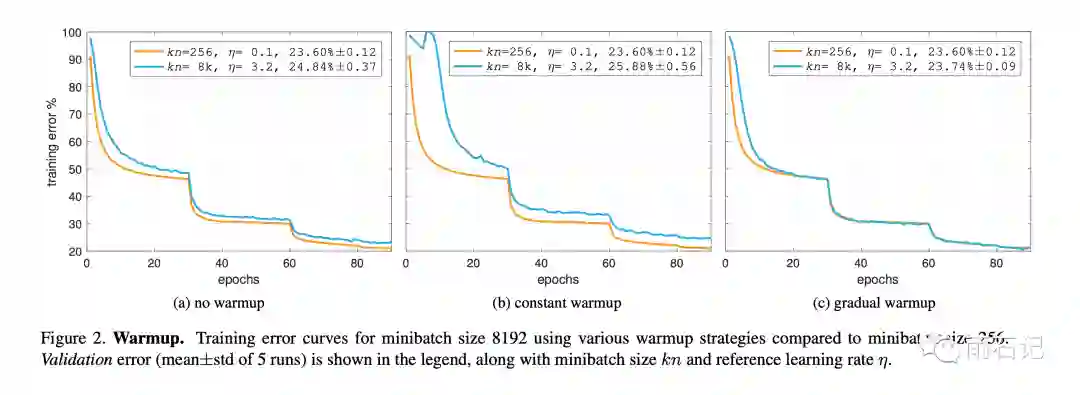
warm-up策略的的比较如下:

可以看到，渐变warm-up得到的训练曲线几乎和单GPU一步步训练一样。

还有很多其他实验结果，感兴趣的同学可以去关注原论文。

总结

这是一篇实验性的论文，但是开启了一个潮流。这里最大的batch_size可以到达8k，后面还有可以到32k/64k的算法。这里的算法是在ResNet上做的，后面还有在Bert上做的。这里的训练时间是1小时，后面还有分钟级的改进。欢迎关注公众号【雨石记】，继续学习后面的内容。

参考文献

[1]. Goyal, Priya, et al. "Accurate, large minibatch sgd: Training imagenet in 1 hour." arXiv preprint arXiv:1706.02677 (2017).

欢迎加入AINLP技术交流群

进群请添加AINLP小助手微信 AINLPer（id: ainlper)，备注NLP技术交流

推荐阅读

这个NLP工具，玩得根本停不下来

征稿启示| 200元稿费+5000DBC（价值20个小时GPU算力）

完结撒花！李宏毅老师深度学习与人类语言处理课程视频及课件（附下载）

从数据到模型，你可能需要1篇详实的pytorch踩坑指南

如何让Bert在finetune小数据集时更“稳”一点

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

文本自动摘要任务的“不完全”心得总结番外篇——submodular函数优化

Node2Vec 论文+代码笔记

模型压缩实践收尾篇——模型蒸馏以及其他一些技巧实践小结

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。