这里介绍几篇计算神经学领域的评论文章,论文主要概述理论计算神经学近几年来在多个方面的研究进展。
计算神经学是用理论方法去研究大脑的计算的学科。
这些论文来自于 Neuron 杂志的特刊:「How does the brain work」。
这篇特刊邀请了来自不同研究方向的实验神经学家和理论神经学家来探讨人类大脑的理论,进展和假说。
以下的文章都可以在 https://www.sciencedirect.com/journal/neuron/vol/94/issue/5 里找到。以及本文所有图片均来自于原文章。
论文1:Space-Time Dynamics of Membrane Currents Evolve to Shape Excitation, Spiking, and Inhibition in the Cortex at Small and Large Scales
一个神经元向目标神经元传递冲动,冲动到达目标神经元时转化为膜电流。
由此方式,目标神经元接受到一定的电流后,就会产生强大快速的膜电流,动作电位,或者冲动。
本文主要介绍了各种神经元膜电流与脑区互相刺激所产生的小范围和大范围的活动现象里观察到的规律。
原文链接:https://www.sciencedirect.com/science/article/pii/S0896627317303951
神经元主要分为两种,一种是兴奋神经,另一种是抑制神经。
兴奋神经的冲动到达其受体神经元会使受体神经元膜电流增加,使受体神经元更容易产生并发射冲动信号。
抑制神经元则相反,其冲动到达其受体神经元会使受体神经元膜电流减少,从而受体神经元更难以产生发射给其受体神经元的冲动信号。
在中枢神经里神经网络膜电流的活动分为四种。
第一种是自发的异步不规则冲动状态,第二种是无冲动的状态,第三种是活性冲动的状态,第四种是没有冲动信号的缓慢震荡状态。
这些状态的切换方式有时候是单一的神经元活动可以影响一个神经网络,在别的情况下,一个相邻神经网络的活动也会影响单个神经元的活动。
本文重点介绍在中枢神经内膜电流在前两种状态下小范围和大范围的活动。
自发的异步不规则冲动状态
:
这种状态一般是大脑没有感官信息的输入,比如轻微麻醉状态下的动物,或者被皮质其他区域的网络自发活动带动。
这种自发的情况下,膜电位多是异步地有不规则波动。
并且兴奋神经和抑制神经对膜电位的控制有紧凑的平衡。
大多数神经元不放电。
少数神经元放电频率缓慢,不规则,并且混乱。
抑制神经放电来中和兴奋神经的放电。
在微观尺度上,网络是平衡的,也就是兴奋神经对膜电位的升高和和抑制神经对膜电位的降低形成一种平衡的状态,但是这种平衡也不是瞬间就达成的,否则网络就不会放电,而是一种长期的动态平衡状态。
活性冲动的状态
:
神经网络从自发的异步不规则冲动状态转而到活性冲动的状态需要打破之前紧凑的平衡状态,从而膜电位的波动突破临界进入多数神经元放电的状态。
如果一个脑区进入活性冲动的状态,那么这种活性冲动的状态可以传播到不同等级,不同阶层的别的脑区。
这种状态下的兴奋-抑制平衡就不是紧凑的了,而进入一种延迟的平衡状态。
因为兴奋神经可以快速适应这种状态,而原先用来抑制这些兴奋神经的抑制神经适应性不好,这种平衡被延迟了。
在介观尺度上,一群兴奋的神经元,在一段延迟后,被抑制信号所平衡。
比如下图是一个脑区膜电位导数随时间的变化(红黄绿为兴奋作用,蓝黑为抑制作用),可见初始时的兴奋作用随时间被抑制作用替代,达到延迟的兴奋-抑制的平衡状态。
评论:
在现有的人工神经网络里并没有动态平衡类似的算法,本文所介绍的兴奋神经和抑制神经导致的膜电位动态平衡,不知道该机制对大脑计算有哪一些方面的帮助,以及为什么在不同的状态下他们的活动也不一样。
下一篇文章就介绍了兴奋神经-抑制神经保持动态平衡的状态时对网络的学习的作用。
论文2:The Brain as an Efficient and Robust Adaptive Learner
这篇文章来自 ENS 的 Group for Neural Theory,原文链接:
https://www.sciencedirect.com/science/article/pii/S0896627317304178
大脑里大多数神经元循环递归地连接其他的神经元,并且大多数神经元要通过多层的连接才能到达直接接受感官的神经元和直接控制肌肉运动的神经元。
这种计算架构,如果仅仅是利用相邻神经元之间的可塑性,很难学会像识别感官信息,操控运动这样需要运用大量神经元的任务。
同时,生物实验指出:
神经元的活动是非常消耗能量的,生物体 20% 的能量需要耗在神经信息处理上。
并且,如果只观测单一的一个神经元,会发现单一神经元它发射电信号的变化性非常大,以至于用同一种刺激物导致神经元放电,每一次测量同一个神经元的活动都不一样。
并且,通过测量多个神经元,研究人员发现,单个神经元的活动变化难以用当时在执行的任务或者刺激物来解释,而与其相邻的神经元的活动更能解释该神经元的活动。
那么,表面上来看,大脑用这么多噪音极大,并且相互影响的神经元来计算看起来既没有效率,又浪费能量。
虽然最近许多人工神经网络,比如循环,卷积神经网络在这些方面多有应用。
但是这些算法需要的反向传播的学习方式是不可能在生物脑里实现的 (Feedback Alignmentan 算法除外,但是 Feedback Alignment 至今在高纬度的图像识别应用上还不成功)。
那么大脑里的神经元又是怎么学习的呢?
文章作者认为,这些看似矛盾的脑神经元特性,用两个元素来解释,就能体现大脑里的神经元其实是强大高效的计算元。
一个是神经元相互之间紧凑的兴奋与抑制机制。
另一个是从上到下的错误反馈,改变连接强度和回路的活动。
这样的话,生物神经网络可以对任何一个动力系统的活动进行学习。
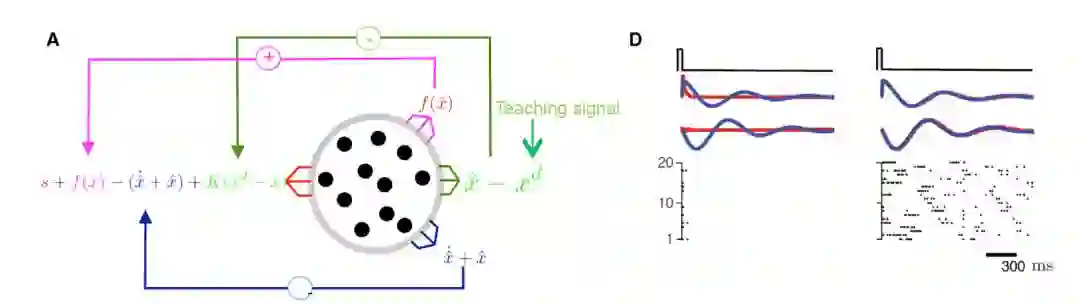
模拟一群神经元,他们接受随着时间变化的输入信息 s,教学信号$x^d$,目的是输出教学信号的近似$x$, 以及所要近似的函数 f(x)。
如上图 A:
神经元的输入是输入信息 s 与输出的函数,对自我动态的预估,和自我活动与教学信号的差值。
这样一群神经元,有了以上的反馈回路,他们学习的目的是使得输入的信号为零,这样就代表系统已经对自我动态,教学信号,以及所要学习的函数有了很好的预测。
这样一群神经元他们同时通过两种时效不同的方式学习,一是通过监督信号$x^d$对于整体神经元反馈来调整连接强度,这一过程相对慢;
二是通过兴奋性神经元和抑制性神经元之间的可塑变化,使得抑制神经活动紧跟兴奋神经,这样学习的过程相对快。
上图 C 中是对于该学习方法模拟的结果。
可见通过学习去近似蓝线,神经元的活动可以从 D 的左图到 D 的右图, 到达神经元活动(红线)近似于蓝线的状态。
评论:
文章作者给出了生物神经网络作为一个动力系统可以对任何一个动态函数近似的思路,并且这种思路可以用来解释上文提到过的动态平衡的计算作用,非常有趣。
论文3:Hierarchy of Information Processing in the Brain: A Novel 'Intrinsic Ignition' Framework
原文来自:
https://www.sciencedirect.com/science/article/pii/S0896627317302404
在这篇评论里,作者提出了一个「自发点燃」的研究思维框架去理解大脑信息处理的不同等级。
"自发点燃」的思维框架是指:
在全脑整合的活动下,信息从空间上的一个本地节点(可以是一个神经元或者一个脑区)通过前馈(feedforward) 或者递归的方式传递到到网络上别的节点的能力。
研究健康的与带有疾病的大脑在认知,感知和运动功能的运算是一个非常复杂的任务,因为大脑里有十亿个递归的,用突触连接的,并且种类各异的神经元。
这些神经元和突触的活动都有很强的非线性特征, 耦合的前馈的和反馈的连接使得大脑成为一个非常复杂的非线性动力系统。
至今研究大脑这样的动力系统的主要方式有三种:
一是寻找神经元与大脑执行的任务的相关性。
比如在初级视觉皮层,观察单一的神经元活动与视觉刺激物的相关性。
一旦确定这样的相关性,研究员就可以测试其中的因果关系去了解神经元的功能。
第二个方式是去测量神经元在没有外界刺激情况下的脑区之间的自发性运动。
但是这样的分析只能了解到脑区活动之间的相关性,而非因果关系。
第三则是去干扰系统,主要用在动物实验上,比如用手术方法使神经元病变,或者用电极去刺激神经元。
作者指出,"自发点燃」作为一种大脑固有的干扰,可以作为一种新的研究方式去理解信息是如何在大脑所处的状态下从一个脑区传递到别的脑区。
这样就可以去研究大脑神经网路各个神经元之间在时间与空间上传递信息的能力。
作者提出,「自发点燃」这样的框架可以用来探索神经元之间计算的等级。
虽然现有的神经连接组学可以用图论的方法去研究大脑神经元解刨结构(physical connectivity)的拓扑等级,但是神经元解刨结构上的等级关系不一定能够对应神经元对信息的动态处理的等级关系。
通过「自我点燃」的框架可以研究和回答后者这个很重要的问题。
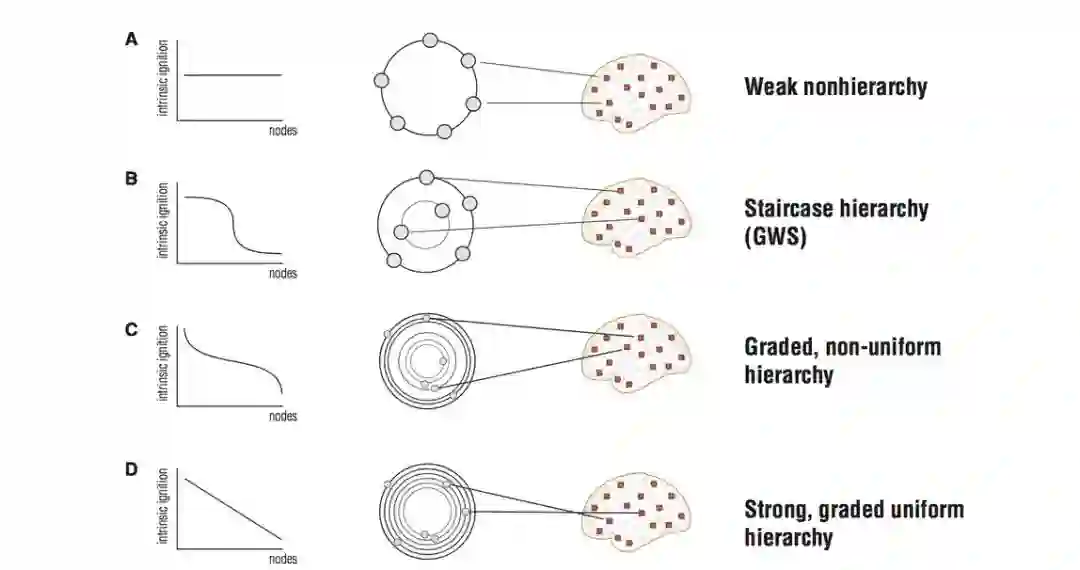
作者将信息处理的等级关系分为几种。
一种极端是计算元于计算元之间不存在等级关系;
每个计算元都有相同的重要性,如上图 A。
另一个极端是强等级关系,并且等级之间是均匀的分层次的,如上图 D。
如果一个神经元在这样线性的等级关系的顶端代表它有最高的「自燃」性,也就是它的活动可以影响到等级较弱的神经元。
在两个极端的等级关系之间有楼梯等级关系,也就是存在较少的等级,并且高级别的计算元「自燃」性更强,低级别的计算元「自燃」性更弱,如图 B。
另外一种是强等级关系,但等级之间层次不均,如图 C。
作者通过对核磁共振数据的分析,总结出大脑在「自发点燃」的情况下更倾向于这一种等级关系。
评论:
作者提出了一个相对新颖的研究框架来理解大脑信息处理。
尤其适用于核磁共振,EEG 等测量大量脑区非侵入性的实验数据。
并且结合图论和复杂网络的理论研究方法,把脑区活动于动物当时的状态结合,可以用来理解很多东西。
以用对于复杂网络以及图论的知识分析信息在大脑之中的传递。
但是作者把大脑信息处理等级分类,并且通过处理 FMRI 数据总结出大脑倾向于强等级关系的结论并不令人惊讶。
毕竟图 C 的等级关系也是是最大熵的等级关系。
论文4:Optimizing Neural Information Capacity through Discretization
原文链接:
https://www.sciencedirect.com/science/article/pii/S0896627317304014
如何去理解像大脑这样复杂的生物系统里面不同的电路,电路元件,蛋白和细胞种类呢?
作者提出可以从以下三点出发,来理解生物系统的计算,并且系统上地解释生物的复杂性:
复杂的系统可以由多个量化的简单系统所构成。
生物系统需要最大化信息传递。
新陈代谢对能量的限制。
理解神经元的计算原理,理论上需要理解一个系统是如何在能量有限的条件下有效地组合量化的信息处理单元去表达系统被输入的在某个范围的信息。
那么怎样组合量化的神经计算元呢?
作者认为,最优的组合形态取决于各个神经元的可靠性和噪声强度。
这里的噪声是指神经元对同一个输入电流反应的噪声,通常神经元会有一定发出电冲动的概率,但是并不是每一次同样刺激条件都会导致同样的结果。
通过组合这样的神经元有两种方式可以得到像逻辑门一样的非线性信息处理元。
一种是冗余编码。
如果每个神经元激发的临界值都很相近,并且遇到外界刺激的反应也相似,那么这些神经元都可以被归作一个类别。
一群这样类似的神经元取平均数,就可以得到比单个神经元更可靠的计算。
另外一种组合方式是各个神经元都有不同的临界值,加权平均各个神经元的活动,这种方式更类似于分布式的编码,尤其适用于需要编码的反应函数和单个神经元的反应函数完全不同的情况下。
冗余编码和分布式的编码 在不同情况下各有优劣。
当每个神经元都有噪音且不可靠的情况下,冗余编码相较于分布式的编码能够传递更多信息。
而当每个神经元的可靠性高于一个临界值时,基于每个神经元都有不同临界值的分布式的编码能传递更多的信息,并且当神经元的临界值分布对应输入的分布的时候,这种信息传递可以最大化。
评论:
这篇文章的作者用一种物理学的思维方式思考神经计算的问题,这种思路深刻并带有启发性。
但是行文缺乏条理,有些类似于在时间压力下写出并发表的。
论文5:Inference in the Brain: Statistics Flowing in Redundant Population Codes
原文链接:https://www.sciencedirect.com/science/article/pii/S089662731730466X
当我们对感知信息进行处理时,我们需要通过高度不确定性的感官信息来推断外部世界的特性。
感知需要用近似的概率推理去从含混的感知数据来推测变量与变量之间的因果关系,并且估算这些特性的概率。
比如当我们伸出手去拿一个杯子的时候,我们并不知道杯子的三维坐标,而是通过对视觉的感应和拿到杯子的感觉来作出这样的行为的。
不确定性是感知系统不可避免的属性,概率推理则是处理这样的信号的最有价值的方法。
那么我们的大脑是怎么去对感知信息进行概率推测的呢。
如果要理解神经元的对概率推测的原理,我们需要理解信息是怎么在非线性的循环递归网络里面传递的。
作者提出,大脑可能在用冗余神经元执行消息传递算法。
运用这种思路可以从以下三个方面去理解神经元的计算。
一方面是感官信息如何「编码」到神经元的活动上。
一方面是神经元的活动模式被「转录」的动态转化。
另一方面是神经信号是如何「解码」去产生行为的。
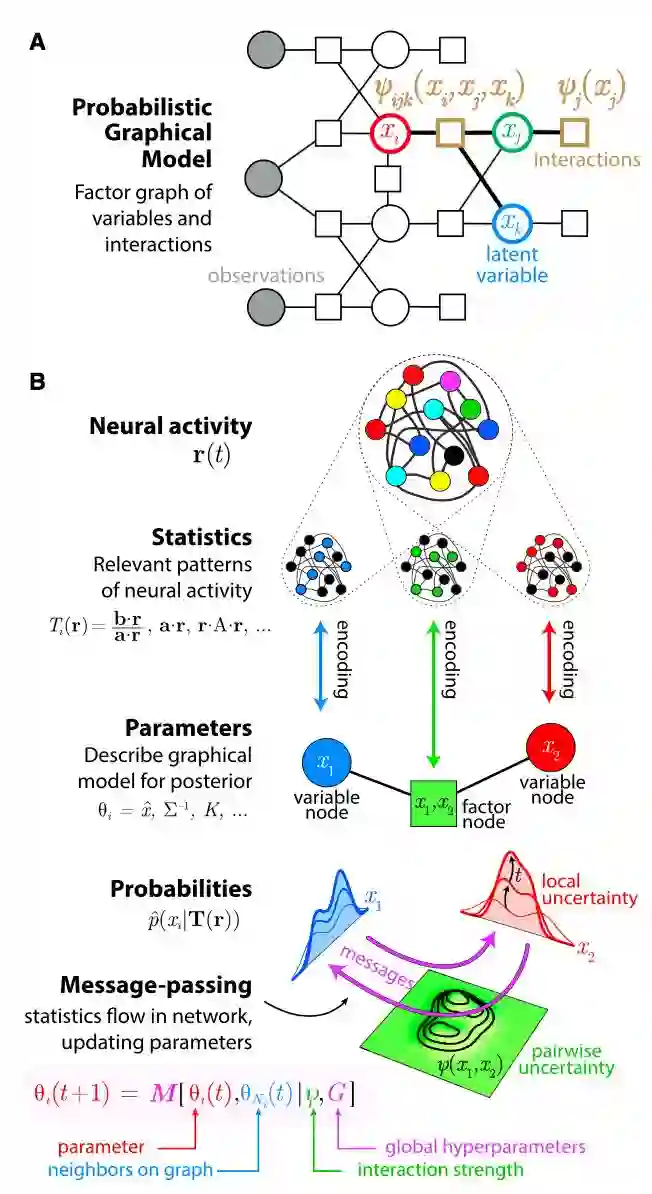
对感官信息的「编码」可以用分布式概率图模型表达。
因为感官世界有着复杂的概率联系。
作者认为,大脑假设只有少量的变量之间有很重要的联系,这种联系可以用概率图模型来表示。
那么这样的概率图模型是如何被神经元的活动来表示的呢?
每一个感官变量的信息传递给和很多对该变量有电冲动反应的神经元。
反过来,同一个神经元可能对多种感官信息都有反应。
作者认为,两者加起来意味着大脑对感官信息的编码是分布式复编码。
通过用一群互相影响的神经元表示概率图模型可以去近似高纬度的概率分布(虽然如何有效地近似还是一个研究领域)。
「转录」表示从神经元的活动模式的动态转化。
大脑需要对信息进行转录来取得有用的信息。
这种转录可以是非线性的,这样一可以独立出与任务相关的隐藏变量,二可以更新用来概率推测的参数。
这样对信息的转录可以用多层信息处理的网络来近似这样的非线性函数,并且这样的处理需要根据不确定性的变化而变化。
那么转录是如何在循环递归的生物神经网络里进行的呢?
作者提出,很可能是通过生物神经元执行的信息传递算法。
这些算法包括 belief propagation, expectation propagation, mean-field inference, 以及一些随机取样算法等等。
神经元的"解码"可以理解为对概率的控制。
这些控制包括有模型的控制和没有模型的控制。
前者表示动物有个自我行为和世界运转的关系的模型,这样的话选择一个好的行为就类似于一个最优的控制问题,动物想要通过对现在以及未来的隐藏变量的推测来最优化获取的奖励。
这样的话概率推测对行为也有指导作用。
后者指动物只是对各种行为和它们的奖励值建立一个查找表。
评论:
感知近似的概率推理这种想法在之前就被休谟,康德以及柏克莱等哲学家就有提到过。
把经验哲学的这一思想和神经学计算结合起来,如果神经网络由感知推断概率图模型,并且神经元活动可以理解为概率取样,这样又可以解释单一神经元活动的随机性,又可以解释感知推理的神经机制。
但是这种假设牵引出许多理论上也未解决的问题,比如作者提出的神经元对感知进行的分布式复编码,它的机制是什么,分布式的计算元又是如何学习一个解释感官世界的概率图模型的。
以及如何在实验上如何验证这样的假设。
这些问题都需要合理的解释。
分析师简介:
Shuchen 目前在图宾根大学人工智能研究所与马克斯普朗克智能系统做研究实习,项目研究如何使深度神经网络的图像识别更接近于人类的视觉识别。
本科物理,计算神经硕士。
主要研究兴趣在于寻找生物学习的的计算模型。
欢迎交流。
✄------------------------------------------------
加入机器之心(全职记者 / 实习生):hr@jiqizhixin.com
投稿或寻求报道:content@jiqizhixin.com
广告 & 商务合作:bd@jiqizhixin.com