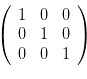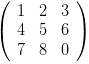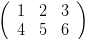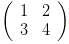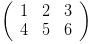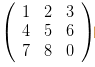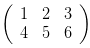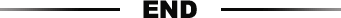大学数学(高数线代)直观理解(二)
本专栏指南:专栏里的每篇文章,我都会大概和包子,可乐,炒菜,火锅……对比一下才会发出来,确保专栏里的每篇文章至少顶两个包子,至多……未知。我想靠推动一下大家学习的进程来自力更生丰衣足食,不知道大家资瓷不资瓷啊?
别误会了,各位,今天我只是邀请大家一起来幻想的。
最简单的大概就是点、线、面、体之类的了。让我们开始幻想,一维空间,二维空间,三维空间……在一个方向上,空间慢慢展开。在两个方向上,让空间慢慢展开。在三个方向上……
这时,如果要我们描述n维空间的概念的话,我们大概会说:所谓一维空间,就是在一个方向上无限扩张(延长)的存在,二维空间,就是在两个方向上无限扩张的存在。而三维空间,说白了就是一个在三个方向无限扩张的存在,那么我们推广到更高的维度,比如n维空间,意思就是一个朝着n个方向无限扩张的存在(只不过这个直观想象不出来)。
以上段落在我刚写的时候,我觉得是浅显易懂,无懈可击的。如果你也这么认为,说明——你还是没动脑筋。
动脑筋的小朋友看了后就问我,小明同学,前/后/左/右是四个方向,你怎么说那是二维呢?
……你是来找茬的???
不过,我们很快能意识到,我们说上述加粗文字的时候,脑中所浮现的“方向”,其实都默认是互不相关的方向,不然的话我们甚至可以说平面在无穷多个方向上扩张——其实也没有错,只是这些方向,都可以被最基础的两个表示出来而已。
怎么表示?你应该想到向量的合成了。如果给你一组向量,里面的向量
不能被其他向量表示出来,那么
(在这个向量组里)就是独立的,是和其他那些不相关的。如果这个向量组里的每一个向量,都不能被这组里其他的向量表示,那么就是说它们都是彼此无关的,这样的向量组叫做极大线性无关组。
话说如果一个向量在这个组里可以被其他成员所表示——那这个向量有卵用……
我不知道大家学的时候是什么感觉,n个彼此无关的向量可以构筑一个n维空间,书上把向量组A的极大线性无关组里面的向量个数叫做向量组A的秩,秩其实就是等级的意思。你向量组A里面彼此无关的向量越多,所构筑的空间维度等级越高。
动脑筋的小朋友又出来了,又指着屏幕说:“你说n个彼此无关的向量可以构筑一个n维空间,具体怎么构筑?好好的n个向量,怎么就构筑成空间了呢?”
哈哈哈哈哈!这真是个好问题,我们得按一定的结构才能筑成空间。我们之前说,n维空间,粗糙地说就是一个在n个(不相关)方向上无限扩张的结构。那么,很显然的,要靠不相关方向能得到相关方向,前提条件是向量可以进行合成才行。而无限扩张说明向量必须得能够缩放吧。合成和缩放,这用代数的观点看,是要我们干嘛?加法和数乘啊!下面就是我们具体把这个空间构筑起来:
首先我们要有个向量组,拿里面线性无关的向量做基。赋予加法和数乘两种运算,两种运算的具体定义如下:
加法:
(1)(交换律)x+y=y+x;
(2)(结合律)(x+y)+z=x+(y+z)
(3)(零元素)在V中有一元素θ,对于V中任一元素x都有x+θ=x;
(4)(负元素)对于V中每一个元素x,都有V中的元素y,使得x+y=θ;
数乘
(5)(1乘律)1x=x;
(6)(结合律)k(bx)=(kb)x;
然后再考虑一下混合运算——
(7)(分配律)(k+b)x=kx+bx;(k倍的缩放加 b 倍的缩放等于k+b倍的缩放)
(8)(数因子分配律)k(x+y)=kx+ky.(合成后再缩放等于缩放后再合成)
k,b等元素属于一个数域P(初学者就理解成R吧)。
好了,数学家拍拍手,这样我们就得出一个向量空间了。
记住这个例子,对于很多人来说,这也许是我们第一次接触数学里”结构“这个概念,而且也许是最后一次。而数学专业的同学以后肯定会再次接触这个概念的。你看,我们这次构筑空间后,至少我们会在直觉里把元素和它们的运算律(映射关系)这些东西和”结构“扯上关系了。下次如果看到什么”代数结构“之类的词也不至于一脸懵逼。
矩阵这个东西实在是个大发明,但其实就表达拿特定的向量所构筑的一个空间。搞个简单的,比如“(1,0,0)(0,1,0)(0,0,1)三个向量所构筑一个三维空间”,这么长一句话的内容其实一个矩阵就表达完了——
嗯……这个是单位阵形式。当然你还可以搞各种花式构筑,比如我们用(1,2,3)(4,5,6)(7,8,9)作为基底一样可以构筑三维空间,表达出来就是这样子的
。不过这些矩阵都是等价的,他们实际上都表示同一个空间,只不过描述方式不一样罢了。
但有的时候,我们会看到这样的
,这个按理说,应该是(1,2,3)(4,5,6)两个向量做基底,构筑的就是二维空间,但它和
不等价。因为从理论上说,既然一个向量,用了三个坐标表示,那意味着我们已经把它放在了一个三维空间里思考,不过这两个向量本身只能构成一个二维空间。所以总的来说,
这个矩阵表示的是一个在三维空间里的二维空间。我们称它表示的是三维空间的一个子空间。三维空间里等级最高为三,像
的等级就达到了满级,而
却没有达到满级。哦,数学里面叫满秩。
任何n阶的满秩矩阵就是n维空间那一定可以表示成n阶单位阵
。事实上,我们知道向量是可以缩放与合成的,比如
是个以(1,2)(3,4)为基的二维空间吧,而这两个基其实完全可以变成(1,0)(0,1),没错吧。怎么变?缩放+合成嘛。也就是用之前说的加法和数乘啊。我们先把(1,2)放大嘛,放大个两倍成(2,4),再反个向得到(-2,-4),然后和(3,4)合成就可以得到(1,0)了,然后再用(1,0)的反向(-1,0)和(1,2)合成,就会得到(0,2),缩放后就是(0,1),OK,基底变换完成。这个就是初等行变换的意思。
基础知识基本就到这里了,也许你还没看够。因为之后的信息量简直要爆炸,我处理三四天了实在没处理得过来,只能放在下一篇了。等价相似特征值,高斯格林斯托克,还有有趣的行列式!这段时间大家多幻想一下空间的扩张,说不定自己就会有奇妙的体验哦。
敬请期待。
往期精彩文章:
长按二维码识别
欢迎大家把独特见解分享出来,投稿邮箱:
math_alg@163.com