Hinton向量学院推出神经ODE：超越ResNet 4大性能优势

2018 年 6 月 21 日 新智元

新智元报道

来源：arXiv

作者：闻菲，肖琴

【新智元导读】Hinton创建的向量学院的研究者提出了一类新的神经网络模型，神经常微分方程（Neural ODE），将神经网络与常微分方程结合在一起，用ODE来做预测。不是逐层更新隐藏层，而是用神经网络来指定它们的衍生深度，用ODE求解器自适应地计算输出。

我们知道神经网络是一种大的分层模型，能够从复杂的数据中学习模式。这也是为什么神经网络在处理图像、声音、视频和序列行动时有很多成功的应用。但我们常常忘记一点，那就是神经网络也是一种通用函数逼近器，因此，神经网络可以作为数值分析工具，用来解决更多的“经典”数学问题，比如常微分方程（Ordinary Differential Equation，ODE）。

2015年横空出世的残差网络ResNet，已经成为深度学习业界的一个经典模型，ResNet对每层的输入做一个reference，学习形成残差函数，这种残差函数更容易优化，使网络层数大大加深。不少研究者都将 ResNet 作为近似ODE求解器，展开了对 ResNet的可逆性（reversibility）和近似计算的研究。

在一篇最新的论文里，来自多伦多大学和“深度学习教父”Geoffrey Hinton创建的向量学院的几位研究者，将深度学习与ODE求解器相结合，提出了“神经ODE”（Neural ODE），用更通用的方式展示了这些属性。

他们将神经ODE作为模型组件，为时间序列建模、监督学习和密度估计开发了新的模型。这些新的模型能够根据每个输入来调整其评估策略，并且能显式地控制计算速度和精度之间的权衡。

将深度学习和常微分方程结合在一起，提供四大优势

残差网络、递归神经网络解码器和标准化流（normalizing flows）之类模型，通过将一系列变化组合成一个隐藏状态（hidden state）来构建复杂的变换:

其中，。这些迭代更新可以看作是连续变换的欧拉离散化。

当我们向网络中添加更多的层，并采取更少的步骤时会发生什么呢？在极限情况下，我们使用神经网络指定的常微分方程（ODE）来参数化隐藏单元的连续动态：

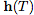
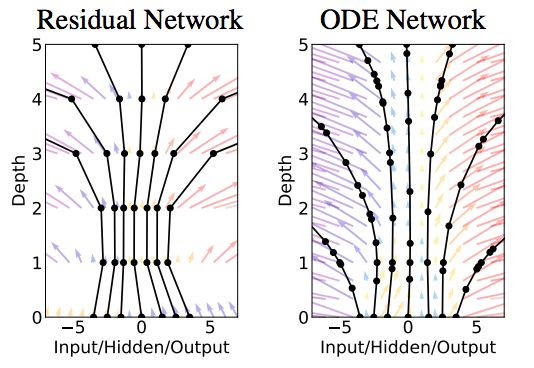
从输入层开始，我们可以将输出层定义为在某个时间时这个ODE的初始值问题的解。这个值可以通过黑盒微分方程求解器来计算，该求解器在必要的时候评估隐藏单元动态，以确定所需精度的解。图1对比了这两种方法。

图1：左：残差网络定义一个离散的有限变换序列。右：ODE网络定义了一个向量场，它不断地变换状态。圆圈代表评估位置。

使用ODE求解器定义和评估模型有以下几个好处：

内存效率。在论文第2章，我们解释了如何计算任何ODE求解器的所有输入的标量值损失的梯度，而不通过求解器的操作进行反向传播。不存储任何中间量的前向通道允许我们以几乎不变的内存成本来训练模型，这是训练深度模型的一个主要瓶颈。
自适应计算。欧拉方法（Euler’s method）可能是求解ODE最简单的方法。现代的ODE求解器提供了有关近似误差增长的保证，检测误差的大小并实时调整其评估策略，以达到所要求的精度水平。这使得评估模型的成本随着问题复杂度而增加。训练结束后，可以降低实时应用或低功耗应用的精度。
参数效率。当隐藏单元动态（hidden unit dynamics）被参数化为时间的连续函数时，附近“layers”的参数自动连接在一起。在第3节中，我们表明这减少了监督学习任务所需的参数数量。

可扩展的和可逆的normalizing flows。连续变换的一个意想不到的好处是变量公式的变化更容易计算了。在第4节中，我们推导出这个结果，并用它构造了一类新的可逆密度模型，该模型避免了normalizing flows的单个单元瓶颈，并且可以通过最大似然法直接进行训练。
连续时间序列模型。与需要离散观测和发射间隔的递归神经网络不同，连续定义的动态可以自然地并入任意时间到达的数据。在第5节中，我们构建并演示了这样一个模型。

ODE求解器提供了一个通用的反向传播算法

论文作者、多伦多大学助理教授David Duvenaud表示，他们通过ODE求解器，提供了一个通用的backprop，但他们的方法是从可逆性上入手，而不是在ODE求解器的运算里进行反向传播（因为这样做对内存消耗很大）。这个方法已经添加到 autograd。

另一位作者、多伦多大学的博士生Tian Qi Chen也表示，他们这项工作创新的地方就在于提出并且开源了一种新方法，在自动微分的框架下，将ODE和深度学习结合在一起。

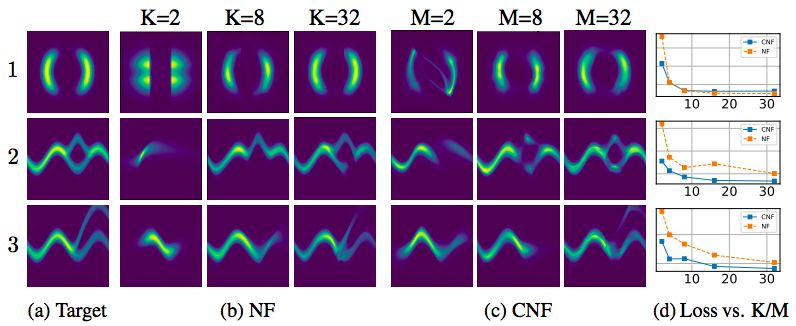
此外，这项研究还得到了很多意外的收获。例如，构建了连续标准化流（continuous normalizing flows），可逆性强，可以使用宽度，就像 Real NVP一样，但不需要对数据维度分区或排序。

标准化流与连续标准化流量的比较。标准化流的模型容量由网络的深度（K）决定，而连续标准化流的模型容量可以通过增加宽度（M）来增加，使它们更容易训练。来源：研究论文

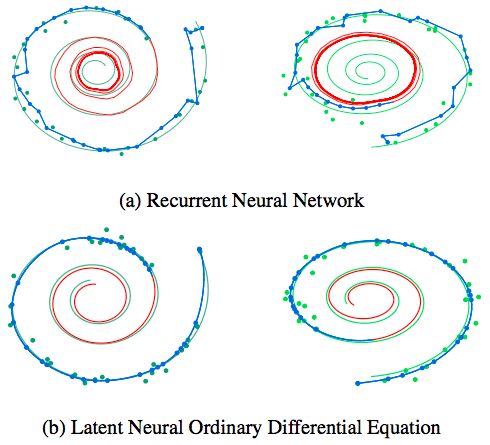
还有时间连续RNN（continuous-time RNNs），能够处理不规则的观察时间，同时用状态依赖的泊松过程近似建模。下图展示了普通的RNN和神经ODE对比：

Tian Qi Chen说，他尤其喜欢变量的即时改变，这打开了一种新的方法，用连续标准流进行生成建模。

目前，作者正在讲ODE求解器拓展到GPU上，做更大规模的扩展。

论文：神经常微分方程

摘要

我们提出了一类新的深度神经网络模型。不在隐藏层中指定离散序列，而是用神经网络来对隐藏状态的导数进行参数化。网络的输出使用一个黑箱微分方程求解器来计算。这些连续深度（continuous-depth）模型具有常量存储成本，根据每个输入来调整其评估策略，并且可以显示地（explicitly）牺牲数值精度来获取速度。我们在连续深度残差网络和连续时间潜变量模型中证明了这些性质。我们还构建了连续标准化流（continuous normalizing flows），这是一种可以用最大似然法来训练的生成模型，无需对数据维度进行分区或排序。至于训练，我们展示了在不访问其内部操作的情况下，对任意ODE求解器进行可扩展反向传播的过程。这使得我们能在较大的模型里对ODE进行端到端的训练。

参考资料 & 了解更多：