[ATCE] 无限宽网络的背后

坐在马桶上，端着一本书，陷入了沉思，我第一次知道无限这个词到底是什么时候？

思绪不由开始扩散，慢慢进入了被我称之厕所贤者时间的状态。正是欧阳修说的“三上”：枕上、马上（温馨提示：开车勿走神）、厕上，中的厕上。

突然灵光闪过，可不就是小学三年级时，每天放学后，打开电视，数码宝贝 OP 刚刚响起：

Wow Wow Wow...

無限大な夢の後の...

我站在沙发上跟着电视机嚎，也只会“wow wow wow”和模糊不清的“无限大”，果然因缘深远，心中一块石头落下，俗话说得好，一通则百通，思想通了，身体也就通了。

果不其然。

“啊~~~”

“ 古池や、蛙飛びこむ、水の音 ”

“哗啦啦啦...”

心满意足地走出厕所。

说起无限，真是数学里一个迷人的话题，直到大学毕业为止也没 get 到它的美。奈何都是被逼着学，只是死记硬背什么泰勒公式无穷级数，遇到题目暴力套公式。

直到 Master 阶段，某天读到某篇论文，作者给一个运算推至极限，之后用切比雪夫大数定理，推出一个非常简洁的结果，那一刻我瞬间被数学之美电到了，本以为只是用来考试的公式，居然可以被灵活地用在这种地方。

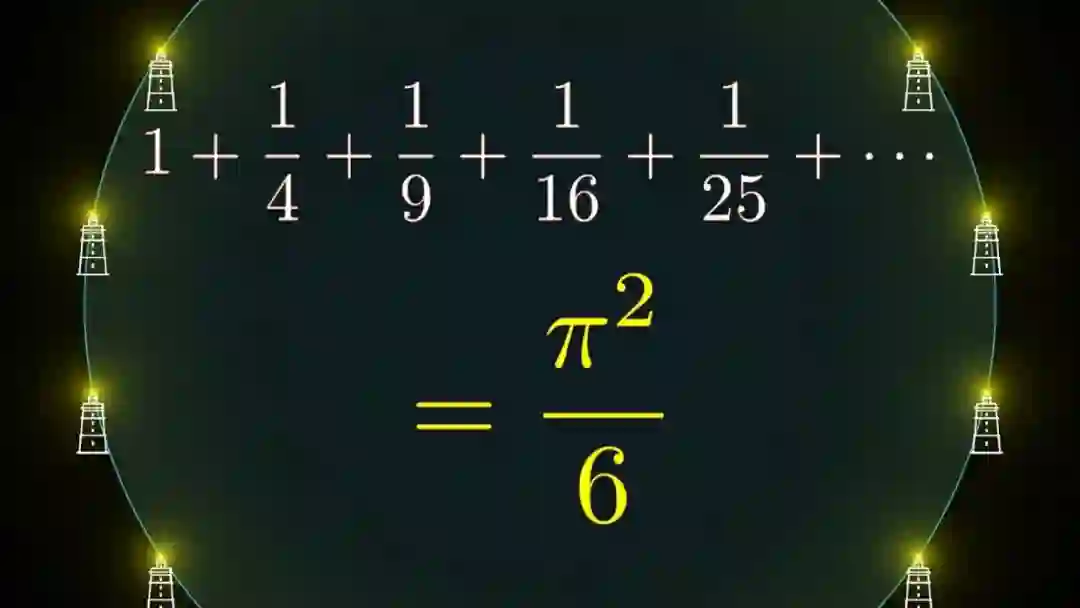
之后关注各种极限，发现用极限看很多东西，会带来一种完全不一样的视角，比如说直线其实只是一个无限大的圆，从此就能很容易的推出巴塞尔问题的解，具体看 3Blue1Brown 的 why  系列。

于是带着极限的视角来看神经网络也是，根据最近研究发现，神经网络参数增加时，一开始确实会和大家预期的差不多，overfitting 然后测试误差增大。

image.png

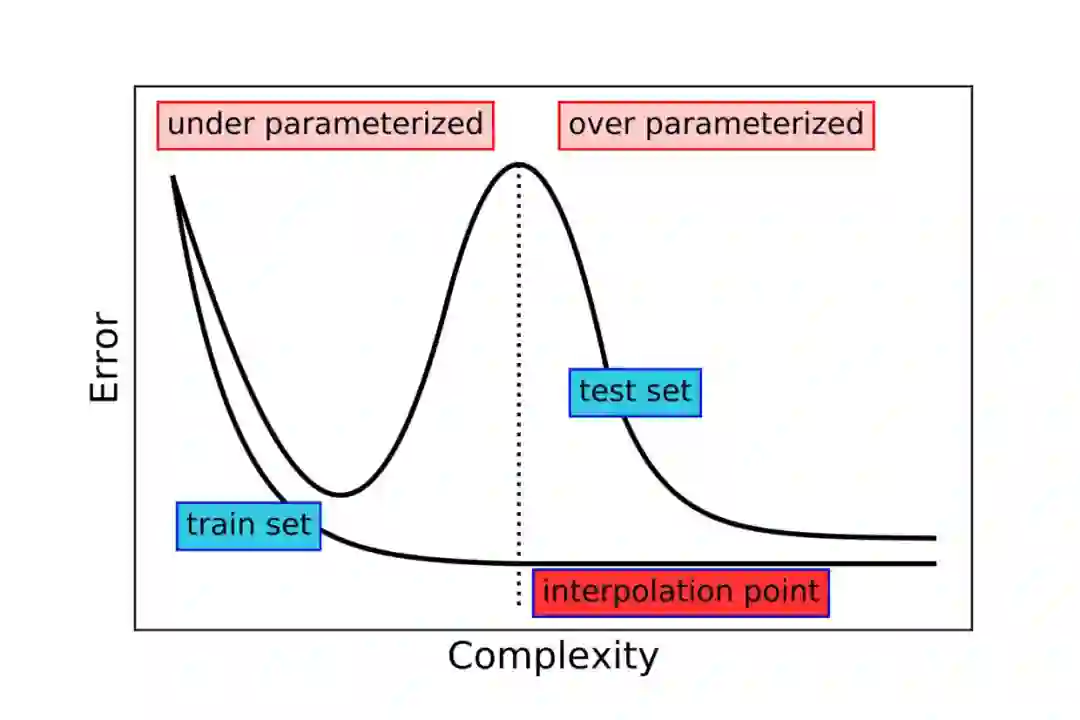
但当我们继续增加神经网络参数时，却发现还没完，测试误差又下去了，这就是之前引起很多兴趣的“double descent”现象。此外，还发现大模型有其他一些特性，比如大模型比小模型训练速度更加快，效率更高，这个可以参考我之前这篇：

同时，大模型在实际应用中也确实取得非常好的效果，于是大家也就不免会问出，如果网络无限大的话会怎么样？

如果网络无限宽

那么大的话就有两个方向，一个是变宽，一个是变深，变深是另一个话题了，目前似乎还没有无限深网络研究。但变宽，现在已经得到了很多关注。

当然变宽并不是直接将神经网络的宽度（对全连接层就是神经元数，对卷积层就是通道数）增加到无限大，然后训练，这样的话即使是给全世界的 GPU，TPU，CPU 什么放一起也训练不起来。

但与数学物理里很多问题一样，大家发现当在想象中给宽度增加到无限大时，看神经网络的视角突然就变了，神经网络和核方法连接起来了，就像圆就和直线连接起来一般。

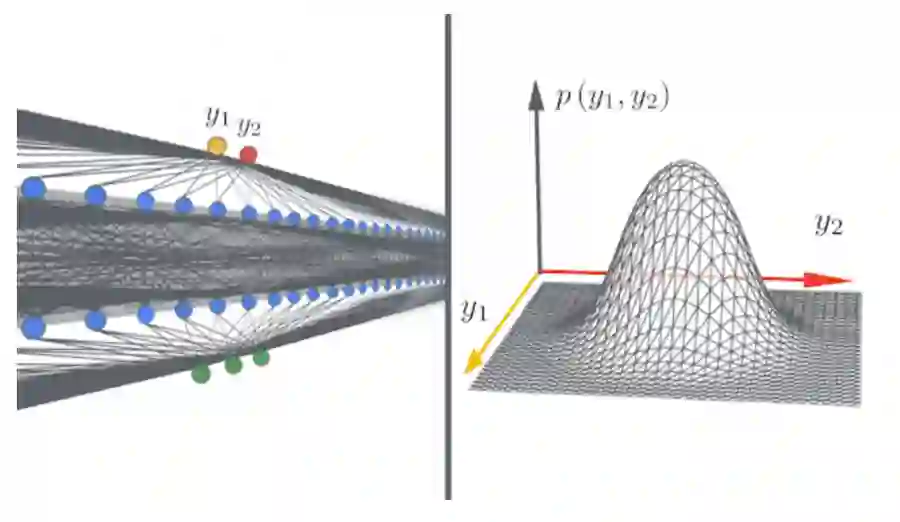
发现通过独立同分布初始化的单层神经网络，在无限宽的假设下，其实就是一个可以从高斯过程(Gaussian Process)得出的函数。

image.png

于是这样的话，我们就不需要实际构建一个真实的无限大网络了，而只需要求出对应的核函数就行。

弱训练的无限宽网络

首先来看最初的研究，研究人员发现了对应低层随机初始化无限宽网络加上顶层经过训练的分类层的核函数，因为底层是随机初始化参数的，所以才被称为弱训练的。

具体推导过程可以参考 [4,5] 论文。

结论是，对应上述无限宽网络的核函数为

其中  为有着  为参数的神经网络对  的输出， 则是  随机化的分布，一般就是限定范围内的高斯分布。这里  是另一个输入。

但问题是，这里对应的时底层未训练的无限宽网络，而我们当然希望真正能得到经过训练的网络。

NTK 与训练过的无限宽网络

于是，接着另一篇论文发现了一种叫做  neural tangent kernel 的核函数可以对应所有层经过梯度下降训练的网络。论文中具体的说明是

通过无穷小步长的梯度（即梯度流）下降训练的，经过适当随机初始化的，一个足够宽的神经网络，相当于一个具有确定核的核回归预测器，而这个核就是 neural tangent kernel (NTK)。

而这个核函数公式为

与前一节的核函数不同的是，NTK 是通过神经网络输出相对参数的求导之间的内积来定义的。

为什么一个经过训练，理应是动态的网络可以通过一个静态的核来估算呢，其中一个 intuition 是，在训练网络时大家发现，当将网络宽度增大，网络越大，经过训练后每个权重相对初始化的改变就越小，那么往无限大推想的话，是不是网络无限大时，经过训练后的权重和初始后的权重就没差。

具体可以参考原始论文[6]和这篇非常好的博文[7]。

至于为什么叫 tangent，应该是跟 tangent linear approximation 的思想一致的原因吧。

NTK 性能与工具

现在很多论文以及在各种任务对无限宽网络以及正常网络进行了对比，但目前还都是在很简单的网络结构下，而且在这样条件下，正常网络还是要比利用 NTK 的无限宽网络要好。

所以这里一定还有 gap 存在于理论和实际中，比如说有什么样的 trick 适用于无限宽网络，可以提高它们性能，当然还有如何将正常网络的各种部件转换成核形式，之后进行对比。

相信大家也发现了其实所谓无限宽，更多是将无限宽网络转换成对应的核形式。

而对于这个，google 最近开源了一个基于 JAX 的工具 neural tangents，将很多无限宽网络转换成核形式给自动化，这样子就不需要花大量时间手动去算实际对应的复杂的核函数（我会说看这些论文，推导部分我都是跳过的吗）。

Reference

[1] Ultra-Wide Deep Nets and the Neural Tangent Kernel (NTK)

[2] On Exact Computation with an Infinitely Wide Neural Net

[3] Fast and Easy Infinitely Wide Networks with Neural Tangents

[4] Priors for Infinite Networks

[5] Deep Neural Networks as Gaussian Processes

[6] Neural Tangent Kernel: Convergence and Generalization in Neural Networks

[7] Understanding the Neural Tangent Kernel

推荐阅读

AINLP年度阅读收藏清单

世界读书日，我来凑个单，推荐几本NLP/推荐算法/广告系统/其他相关的新书

百度PaddleHub NLP模型全面升级，推理性能提升50%以上

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

当当的羊毛，快薅，这一次要拼手速！

数学之美中盛赞的 Michael Collins 教授，他的NLP课程要不要收藏？

自动作诗机&藏头诗生成器：五言、七言、绝句、律诗全了

From Word Embeddings To Document Distances 阅读笔记

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

这门斯坦福大学自然语言处理经典入门课，我放到B站了

可解释性论文阅读笔记1-Tree Regularization

征稿启示 | 稿费+GPU算力+星球嘉宾一个都不少

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。