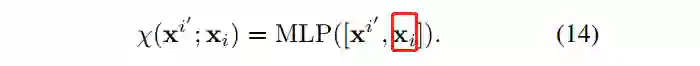AAAI 2022 | 条件局部图卷积网络用以气象预测

©PaperWeekly 原创 · 作者 | 西南交一枝花

单位 | 西南交通大学CCIT实验室

研究方向 | NLP、时空数据挖掘

本次分享的是 AAAI 2022 一篇来自西湖大学的气象预报工作《Conditional Local Convolution for Spatio-temporal Meteorological Forecasting》。

作者单位也对此论文进行了相关解读。还对此解读的原因有两点：1）链接中的解读介绍的过于泛泛，没有看到问题转化的过程；2）自己也在做这块研究，同一个研究任务学习一下看待问题的角度以及相应的解决方法。

整体来说，该文针对气象预测任务提出了一种条件局部时空图网络，从球面气象信号特性切题，依据到图神经网络面向非规则数据的特征表达能力，考虑到气象流动的区域性以及，设计局部条件的图卷积核计算单元。

本文的介绍顺序与原文有些类似，不过有些概念为方便理解提前给出。时空预测挑战--->研究动机--->问题定义，相关概念--->方法介绍---->实验。

时空气象预测任务面临两大挑战

1. 非规则分布传感器采集到的气象信号不同于平面栅格类图像，不适用于 CNN 类网络。比如，温度传感器在海洋或陆地上不均匀分布，不是固定结构的网格位置。此外，气象数据通常是球面信号不是平面信号。之所以说气象数据是球面信号，依据是气象信号反映的地球表面的状态，地球表面是球面。

2. 高维时序和空间依赖难以建模动态性。比如，不同的地形地貌表现出完全不同的风流或温度传播模式，另外，极端气象变化导致气象时序信号的非平稳性。

针对以上两点，补充说明的是，除本文外，笔者并未搜索到气象信号视为球面信号的工作，有了解的欢迎补充。关于第二点，对于 AI for environment science 是一个难题，环境科学是一个复杂的开放环境，难以对其完整建模，只能做简化。以不同地形、地貌表现不同的气象状态为例，有时候隔一个山头（空间距离并不远）可能温度差别很大，确实很难建模。通过数据探索空间两个点所处地形的联系，还是比较困难，可以引入先验知识指示模型区分不同点的属性。

研究动机

1. 图神经网络在非规则时空预测任务上取得较好的表现，如交通流预测、空气质量预测等；

2. 气象流在不同局部区域表现差异较大。

通过上述两点的分析，作者想要建立一种图卷积核，它可以感知不同位置区域进行相应计算，用于近似和类比真实环境下不同区域的局部气象模式。

因此，基于位置特性的平滑性假设，提出了局部条件核，将其嵌入到基于图卷积的循环网络，图卷积同时考虑两个节点之间的距离和相对方向。

在文中 4.3，给出了该假设的解释。气象信息流动的局部模式具有平滑性，也就是，两个相近的节点在从它们的邻居聚合信息的模式应该是相似的。

下面，我们来看本文是如何定义位于球面气象信号的时空预测任务。

问题定义&概念定义

输入&输出：给定 t 时刻，N 个位于球流形 的气象信号，可以将其表示为图 记录了 N 个节点的位置。球面可以视为 的子集，所以每个节点位置包括了 ，并且 。 表示边的几何，A 表示邻接矩阵。N 个信号在 t 时刻的气象观测值可以表示为 ，D 表示气象因子的个数：

由于数据集不存在邻接矩阵，本文计算两两之间的球面距离，然后再通过 K 近邻聚类。

补充一下，wiki上的概念，流形是可以局部欧几里得空间化的拓扑空间，是欧几里得空间中的曲线、曲面等概念的推广。地球表面是一个稍微复杂的流形。球面（球流形）由一群二维图形表示，称为二维流形。想要进一步了解，可以查阅：

https://www.wanweibaike.net/wiki-流形

图卷积计算没有特别说明，沿用了 DCRNN 的计算形式，除了论文特别提及的卷积核的数值应该对于着重影响气象变化的邻居节点上更大。比如，从东南往西北方向流动的热流，应该给与东南方向的节点更大的权重。（感觉难以实现，首先数据上不支持，其次在卷积中如何依据此类知识动态赋予权重）

概念

1. 球流形，地球表面的信号可以看作是球面信号，所以引入了球流形便于卷积计算，由于卷积操作是在平面上进行的，论文定义了局部空间，又称为 M-D 欧式空间，认为一般性的卷积可以在此局部空间计算。

2. 局部空间，是指以节点 x 为中心的局部欧式空间。

3. 球表面两点距离计算。great-circle 距离，也称为球面距离，可参考 https://en.wikipedia.org/wiki/Great-circle_distance。在计算 K 近邻时需要依据两点间的球面距离。

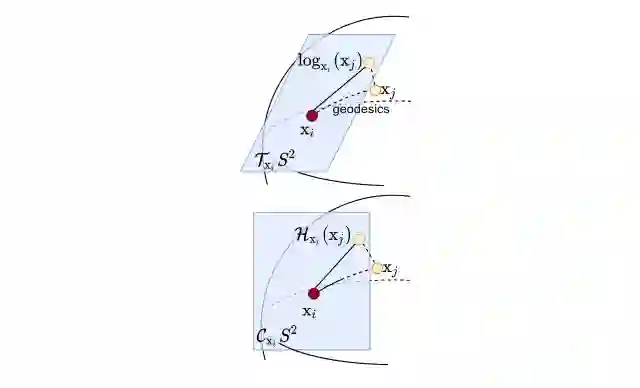
4. 同距映射（isometric map），球表面到局部空间映射，卷积是在平面上进行的，所以引入了局部空间，那么还需要把球表面映射到局部空间。涉及到球面上两个点的距离，映射到局部空间上，两点距离的变化。同距映射需要保证等距映射，即源球表面的距离应该等于映射后的平面距离。

5. 对数映射（Logarithmic map），用于将节点 x 的邻居节点同距映射到局部空间。

6. 局部坐标系统，本质上是为了建立球表面映射到局部空间后节点之间的相对位置或相对方向。具体如何实现的，笔者未从文中看到。

所提方法

4.1 作用于球面的局部卷积

先对不同一般性图卷积进行介绍。文中公式表示图卷积如下：

公式 2、3 是通用的节点表示更新方式，公式 4 中， 表示卷积核，是 ，这里作者应该是想将之前作用在平面的卷积，定义为作用在球流形上的卷积，但仅给出了符号定义，没说明计算上有什么不同，不过笔者没有去看源码，后续有新发现再来补充。基于这种定义，可以看出 是等价于 的，但是文中缺少对 的介绍。

下面看下对于 DCRNN 卷积公式的表示：

▲ DCRNN在本文

以下为 DCRNN 原论文表示：

▲ DCRNN3

两者在计算上是一致的，用来表示带权的邻接矩阵。只不过作者在文中没有从这个角度说明与 DCRNN 的关系。

下面返回到在球表面上做局部卷积操作：

1. 先给出在平面在做局部卷积计算定义，其中关于 k1 和 k2 的介绍，就是对卷积核大小的限定。

2. 将上述卷积扩展到球流形上需要两个操作，通过等距映射将中心节点球表面的邻居映射到局部空间，然后通过建立局部坐标系统，使得邻居节点保持原有的相对方向。

如公式 10 和 11 所示，除等距映射和局部坐标系统外， 表示卷积核。

下面对如何构建局部坐标系统，如何实现等距映射以及局部卷积核的具体实现进行介绍。

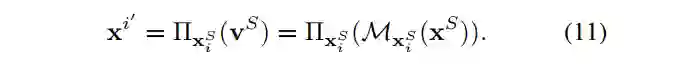
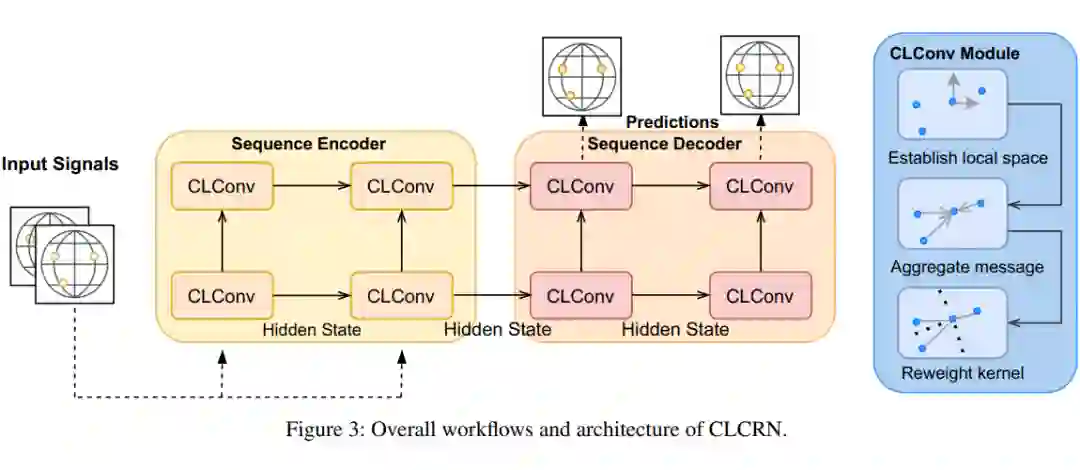
4.2 局部空间构造

首先，引入圆柱正切空间（cylindrical-tangent space）和水平映射（horizon map），使用水平映射将球流形的节点映射到圆柱正切空间。为何不使用正切空间+对数映射，主要是考虑到前者可以保留原有球表面上的相对方向，这点我们在之前有提到过相对方向在气象中的作用。

（上面子图是正切空间搭配对数映射，下面子图是圆柱正切空间搭配水平映射）

举例来说，位于北半球的一个节点，邻居位于它的东方，经过对数映射后，在正切空间上，会变为位于东北方。具体的证明，笔者没有去细究，感兴趣的可以在附录上看证明。

铺垫了这么久，终于要介绍条件局部卷积了。

4.3 条件局部卷积

作者认为局部条件卷积应该具有三个特性：

1. location-characterized，不同中心节点的局部区域，由卷积核抽取的气象特征是不同的。

2. smooth， 空间距离相近的中心节点表现的模式应该是相似的。

3. common，核由不同局部空间的不同邻居空间分布所共享。

下面一个个地介绍三个部分：

首先是位置特性，期望卷积能够自适应学习并模仿每个中心节点局部区域的局部模式。 在更新时使用了邻居信息（仅表示相对位置），这样使得kernel不能捕获局部特点模式。最后解决方法是加上自身节点，一大段介绍，有点封装过度，一句话就能说清楚的事情，考虑了什么问题，所以采用了什么方法。

其次是平滑性，定义为两个相近的节点在从它们的邻居聚合信息的模式应该是相似的。

主要思想是如果节点 和 距离非常近，那么 相似于 。

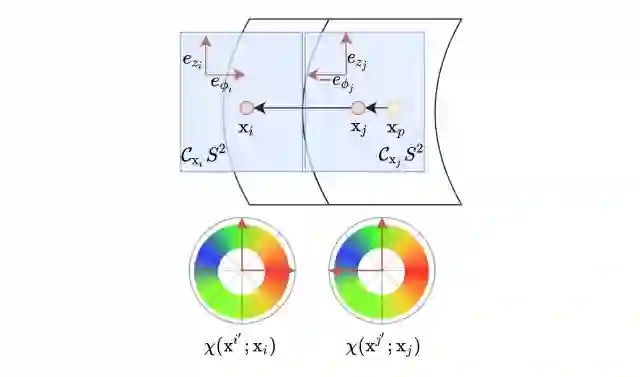
我们先了解下为什么会有正交基？圆柱正切空间是欧式空间的一种，局部空间转化可以通过两个正交基来实现，这点在前面没有介绍，这里补充一下。

作者认为统一标准的正交基选择可以避免平滑性被破坏，原因如下图所示：

▲ 平滑性

节点 i 和节点 j 互为邻居，其所表示的正交基如红色箭头所示。给定球表面上一个点 p 位于两个节点的东方，对节点 i 和节点 j 有较大的气象影响。在局部坐标系统中，第一个坐标如果是正的，另外一个就是负的。如果不是统一标准的正交基，核如果还是平滑的话，p 不会对节点 i 和 j 造成很大影响（这是笔者对原文的意译，但是确实没看懂为何不会产生大的影响（计算值的大小））。

作者使用了全连接网络，使用 tanh 作为激活函数来保持正交基选择的统一标准，这样保证了局部卷积的平滑性。

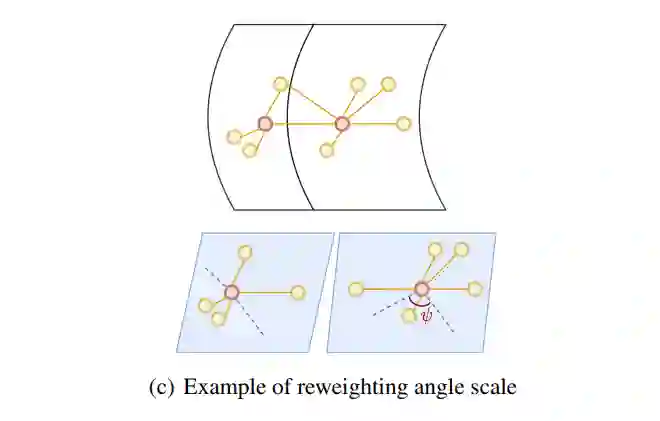
下面介绍如何重新为非规则空间分布赋予权重。动机是考虑离散节点的非规则分布与核函数的连续性冲突。

如下图所示，原文中介绍右边中心节点坐落在西南方的邻居节点有两个，左边中心节点有一个。笔者从图上来看，不是正好相反吗？左边的中心节点西南方（左下方）有两个，右边是一个，没看明白。这个本质上还是每个节点周围拓扑结构不同，不了解为什么需要重新分配权重。文中重新分配权重的依据是综合了角度与距离，将局部坐标转化到极坐标系统，可以同时表示距离和角度。

接下来，介绍为何所提到的局部卷积不适用于交通流预测，也就是说明为何不直接照搬交通流上的图卷积操作到气象预测。

主要论点是交通流模式与气象模式在平滑性上存在较大的不同。比如说两个很接近的区域，由于中间存在重要的交通枢纽出口，交通模式可能存在很大的差异。此外，所提卷积核考虑了方向性，这种机制在交通上没有太大意义。作者还给出了相应的图示：

笔者认为上述两点有些牵强，首先，相邻的区域的气象也有可能有不同的表现，受局部地貌影响，受洋流影响等，环境的复杂性要高于交通流的复杂性；此外，交通流预测也会考虑到方向性的问题，比如某些道路是单行道，双行道，道路的等级之类。

4.4 动态时序建模

讲完空间，现在说到了时序建模，在该方面，论文所介绍地简单些，使用 GRU 来捕获时间特性。令读者迷惑的是，直到这个章节，论文才给出整体结构。（当然，我看的这个版本是 arxiv 上，不知道在 AAAI22 最终版是否有修改），整体结构采用 seq2seq 的方法，没有特别需要关注的地方。

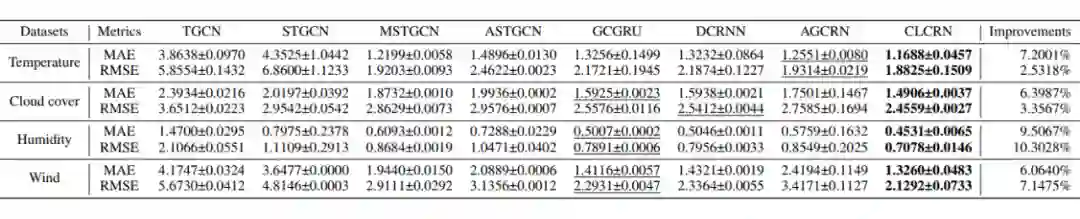
实验

数据集：采用 WeahterBench（2020 发表的一篇论文），包含了 2048 个传感器，本文选择了温度、云量、湿度和地表风分量 四个因子作为预测目标。使用历史 12 个时刻预测未来 12 个时刻。

评测指标：MAE, RMSE, MAPE

对比方法：都是时空图方法，包括 STGCN, MSTGCN, ASTGCN, TGCN, GCGRU, DCRNN, AGCRN。

5.1 总体表现

▲ 总体表现

所提方法表现最好，另外说明了与基于循环网络的方法对比注意力表现更好，所提方法进一步提升了基于循环网络的方法。这几个说明都还没触及到本文的创新点，我们接着往下看。

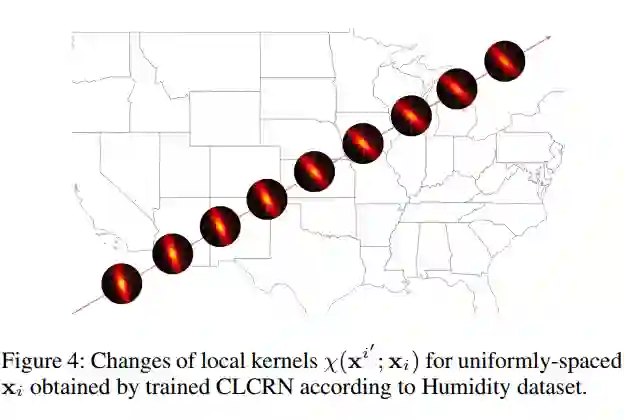
5.2 可视化

▲ 可视化

作者选择美国从西南到东北的线，一些采样点作为中心节点。如上图所示，论文中介绍“从湿度数据中观察到明显的方向性：节点从西北和东南影响中心节点最大。”，作者应该对图中的颜色进行说明个，是否是通过中间区域的扁平范围表示影响，全靠读者来揣测。

5.3 CNN还是RNN

这个实验不太重要，也不是论文的重点，可以往后放一下，不用太靠前。

5.4 水平映射 VS 对数映射

5.5 消融实验

论文针对卷积核中所用到的角度、距离以及 MLP 做了对比。另外还有网络层数，邻居个数，隐藏单元个数的超参实验。

看了实验章节，总体感受还是觉得，实验还是应该集中到所提的卷积核上，通过替换卷积表现出局部条件卷积的优越性；通过对比圆柱正切空间+水平映射 对比 正切空间+对数映射，这些才是论文的核心创新点。

该工作涉及了较多几何学相关的概念，在读的过程中，觉得论文在将工作封装地过于“高大上”，对于简单的思想，介绍地过于复杂（文中有给出示例）。不过，总体来看，作者对于问题的研究还是比较深，能够将地球气象的一些特点与几何空间的概念联系在一起。

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·