AAAI 2018 | 腾讯提出自适应图卷积神经网络，接受不同图结构和规模的数据

2018 年 1 月 21 日 机器之心

选自arXiv

作者：Ruoyu Li等

机器之心编译

参与：路雪

近日，AAAI 2018 发布接收论文列表，腾讯 AI Lab 共入选 11 篇。在论文《Adaptive Graph Convolutional Neural Networks》中，腾讯联合德克萨斯大学阿灵顿分校提出自适应图卷积神经网络 AGCN，可接受任意图结构和规模的图作为输入。

论文：自适应图卷积神经网络（Adaptive Graph Convolutional Neural Networks）

论文链接：https://arxiv.org/pdf/1801.03226.pdf

摘要：图卷积神经网络（Graph CNN）是经典 CNN 的推广方法，可用于处理分子数据、点云和社交网络等图数据。Graph CNN 中的的滤波器大多是为固定和共享的图结构而构建的。但是，对于大多数真实数据而言，图结构的大小和连接性都是不同的。本论文提出了一种有泛化能力且灵活的 Graph CNN，其可以使用任意图结构的数据作为输入。通过这种方式，可以在训练时为每个图数据构建一个任务驱动的自适应图（adaptive graph）。为了有效地学习这种图，我们提出了一种距离度量学习方法。我们在九个图结构数据集上进行了大量实验，结果表明我们的方法在收敛速度和预测准确度方面都有更优的表现。

引言

尽管卷积神经网络（CNN）被证明可成功解决大量机器学习问题（Hinton et al. 2012; Dundar et al. 2015），但是它们通常要求输入为张量。比如，图像和视频被分别建模为 2-D 和 3-D 张量。但是，在很多真实问题中，数据所在的栅格（grid）不规则或者非欧几里德域（non-Euclidean domain），如化学分子、点云和社交网络。相比于规则的张量，这些数据更适合被建构为图，从而能够处理不同的近邻顶点连接性（neighborhood vertex connectivity）和非欧几里德度量。在这种情况下，支持在栅格上进行卷积的平稳性和复合性无法再得到满足。因此，在图结构数据上重构卷积算子是必要的。

但是，把 CNN 从规则栅格扩展到不规则栅格并不容易。为了简洁地构建卷积核，早期 Graph CNN 假定数据仍然是低维的（Bruna et al. 2013; Henaff, Bruna, and LeCun 2015）。由于卷积器根据节点度（node degree）区别处理各个节点，卷积核过分关注于局部而不灵活，无法学习复杂图（带有无法预测且灵活的节点连接性，如分子和社交网络）的层次表征。

当前 graph CNN 遇到了以下瓶颈问题：

图度（graph degree）受限；
输入数据必须共享同样的图结构；
图固定，且非通过训练学得；
无法从拓扑结构中学习。

本文提出了一种新型频谱图卷积网络（Spectral Graph CNN），输入可以是多种图结构的原始数据，如包含不同数量苯环的有机分子。因此，该网络不使用共享频谱核，而是给批量中的每个样本一个特定的图拉普拉斯矩阵（Graph Laplacian），客观描述其独特拓扑结构。根据其独特的图拓扑，定制化图拉普拉斯算子将带来定制化的频谱滤波器。

研究哪种图最适合某种监督学习任务是很有意思的。例如，化学键自然地为化合物构建出一个内在图。但是，它无法保证内在图上的卷积器能够提取所有有意义的特征。因此，我们训练了一个「残差图」（residual graph）以发现内在图不包含的残差子结构。此外，为了确保残差图是特定任务的最佳补充，我们设计了一个机制在训练其余 Graph CNN 时学习残差图。

我们在多个图结构数据集上验证本文提出的频谱卷积网络，数据集包括化学分子、LIDAR 生成的点云。Graph CNN 的创新之处如下：

1. 构建独特的图拉普拉斯算子。为一个批量中的每个样本构建和学习独特的残差拉普拉斯矩阵，将学得的残差图拉普拉斯算子添加到初始图上。

2. 学习用于生成残差图的距离度量。通过学习共享的最优距离度量参数，图的拓扑结构随着预测网络的训练而更新。学习的复杂度独立于输入规模，成本仅相当于。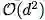

3. 卷积中的特征嵌入。在卷积前，先进行顶点特征变换，使得顶点内不同特征之间和不同顶点特征均联系起来。

4. 接受灵活的图输入。由于 1 和 2，本文提出的网络可以输入不同的图结构和图大小，对图度没有限制。

方法

SGC-LL 层

SGC-LL 层的运算如算法 1 所述：

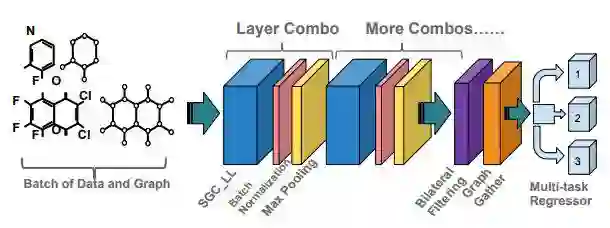
AGCN 网络

图 3：AGCN 网络配置。把原始图结构数据和初始图直接输入该网络。

结论

我们提出了一种新型的基于自适应图的频谱图卷积器（SGC-LL）。SGC-LL 学习最优距离度量和特征变换，进而学习残差图拉普拉斯矩阵（Residual Graph Laplacian）。目前，AGCN 是首个允许任意图结构和规模的频谱 Graph CNN。残差图拉普拉斯的监督式训练使得模型更适合预测任务。在不同图结构数据上的大量多任务学习实验表明，不同预测任务上 AGCN 优于之前顶尖的 Graph CNN。