Google AI 普林斯顿：当前和未来的研究

2019 年 1 月 8 日 谷歌开发者

文 / Elad Hazan 和 Yoram Singer，Google AI 和普林斯顿大学研究员

Google 长期与学术界合作推动研究，并与全球多个大学在合作研究项目上开展合作，从而在计算机科学、工程和相关领域中取得了新的进展。今天我们宣布，最近的学术合作将在新的实验室中开展，该实验室与普林斯顿大学历史悠久的拿骚楼 (Nassau Hall) 仅一街之隔，将于明年初开始启用。通过促进与普林斯顿大学师生更紧密的合作，此实验室旨在扩展机器学习领域多个方面的研究，初期的研究工作主要侧重面向大规模机器学习、控制理论和强化学习的优化方法。下面我们简要介绍一下迄今为止的研究进展。

大规模优化

想象一下，您正在山中徒步旅行并且用光了水。您需要到湖边去。如何才能最高效地到达湖边？这是一个路线优化问题，类似于数学中的梯度下降法。因此，您向最速下降方向移动，直到在路线尽头找到最近的湖泊。如果用优化的语言表述，湖泊的位置称为（本地）最小值。梯度下降轨迹与下图所示路径相似，一个口渴的徒步旅行爱好者会按照这一路线尽快赶到湖边。

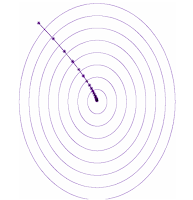
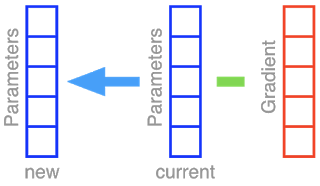
梯度下降 (GD) 及其随机版本随机梯度下降 (SGD) 是用于优化神经网络权重的选择法。通过将全部参数堆叠在一起，形成一组组合成向量的单元格。我们简单观察一下，然后假设我们的神经网络只有 5 个不同的参数。采取梯度下降步骤意味着从当前参数组（蓝色）中去除梯度向量（红色），并将结果放回到参数向量中。

回到我们的徒步旅行爱好者身上，我们假设她在向下张望时凭借有限的能见度发现了一条未经标注的路，这条路又长又窄。如果遵循下降法，她的下山路径将会呈之字形，如下方左侧插图所示。但现在，通过利用地形的倾斜几何构造，她的下山进程可以更快。也就是说，相比于向两边移动，她可以前进更多距离。在梯度下降的语境中，我们将 “加快步伐” 称为 “加速”。斯坦福大学的 John Duchi 教授在 Google 工作时，我们合作设计了 AdaGrad 算法，并在此算法中首次提出了一类非常受欢迎的加速方法，名为自适应正则化（或自适应预处理）。

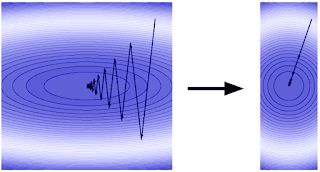
此方法旨在改变优化目标景观的几何结构，从而使梯度下降法更容易发挥作用。为此，我们采用预处理方法拉伸和旋转空间。经过预处理的地形看起来仿佛右上方图片中平静的湖面，是一个近乎完美的球形，而下降轨迹则是一条直线！从程序上来看，相比于从参数向量本身去除梯度向量，自适应预处理首先通过一个名为矩阵预处理器的 5×5 多单元格结构增加梯度，如下图所示。

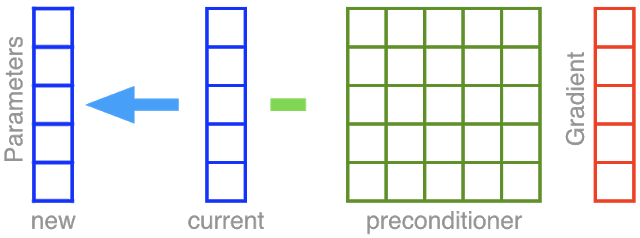
这项预处理操作生成了一个经过拉伸和旋转的梯度，然后我们像之前一样，去除其中的梯度向量，从而加快前往湖边的进程。然而，预处理存在一个弊端，即它的计算成本。与从 5 个单位的参数向量中去除 5 个单位的梯度不同，预处理变换本身需要 5×5=25 次运算。假设我们要预处理梯度，以便使用 1000 万参数学习深度网络。单单一个预处理步骤就需要 100 万亿次运算。为了节省计算，我们还在关于 AdaGrad 的论文原稿中介绍了对角版本，其中的预处理相当于无旋转拉伸。之后研究人员采用并修改了对角版本，从而产生了另一个非常成功的算法，叫做 Adam。

这种简化的对角预处理使梯度下降仅需承担边际额外成本。但过分简化也有弊端：我们无法再旋转空间。回到我们的徒步旅行者，如果又深又窄的峡谷呈东南至西北走向，那么她将无法再向西跃进。如果我们向她提供一个“受到操纵”的指南针，即北极在西北方向，她就可以遵循之前的下降步骤了。在高维度中，对指南针操纵的模拟是全矩阵预处理。因此，我们自问能否设计一种预处理方法，该方法允许进行相当于坐标旋转的操作，同时可以保持计算效率。

在 Google AI 普林斯顿，我们开发了一种进行全矩阵自适应预处理的新方法，该方法的计算成本与常用的对角限制大致相同。您可以在论文中找到详细信息，但我们会在下面描述方法背后的核心思想。我们没有使用全矩阵，而是用三个矩阵的积来代替预处理矩阵：高瘦型矩阵、（小）正方矩阵和矮胖型矩阵。我们使用较小的矩阵执行大量运算。如果我们有 d 个参数（而不是单个大型 d × d 矩阵），则由 GGT（Gradient GradientT的简写形式）维护的矩阵和提出的方法大小分别为 d × k、k × k、k × d。

对于可以被当做算法 “窗口大小” 的 k 的合理选择，计算瓶颈已经从单个大型矩阵减为小得多的 kk 矩阵。在实现过程中，我们通常将 k 选择为 50，维护较小的正方矩阵其开销要低很多，同时却能产生良好的实证性能。与处理标准深度学习任务的其他自适应方法相比，GGT 可以与 AdaGrad 和 Adam 媲美。

用于控制和强化学习的频谱滤波

Google 研究团队在普林斯顿的另一个主要任务是为决策系统开发有原则的构件块。具体而言，该团队在努力利用在线学习领域的可证明保证，研究决策算法在不确定状态下的鲁棒性（最坏情况）保证。如果一个在线算法事后学会了制定决策和最好的 “线下” 决策，则我们说它会获得无悔保证。该领域的观点已推动了理论计算机科学的许多创新，并为研究应用广泛的 Boosting 技术提供了简练的数学框架。我们设想利用在线学习的理念来扩展现代强化学习的工具包。

抱着这一目标，通过与普林斯顿大学研究人员和学生的合作，我们为线性动态系统的估算和控制开发了频谱滤波算法技术（参见 https://openreview.net/forum?id=BygpQlbA-）。这样一来，就可以从未知来源传输有噪观察值（例如，位置传感器测量值）。信号源作为一个系统，其状态会遵循一组线性方程（例如牛顿定律）随着时间的推移发生演变。要预见未来的信号（预测），或者执行将系统带入预期状态的操作（控制），常用方法是从明确地学习模型开始（一种称为系统识别的任务），但这种方法往往缓慢且不准确。

通过将预测和控制重新表示为凸计划，频谱滤波可以规避明确模拟动态情况的需求，从而实现可证明的无悔保证。新的信号处理转换是这项技术的重要组成部分。其理念是使用定制的滤波器组通过卷积来总结过去输入信号的较长历史记录，然后使用此表征预测动态系统的未来输入。每个滤波器通过采用此前输入的加权组合，将输入信号压缩为单个实数。

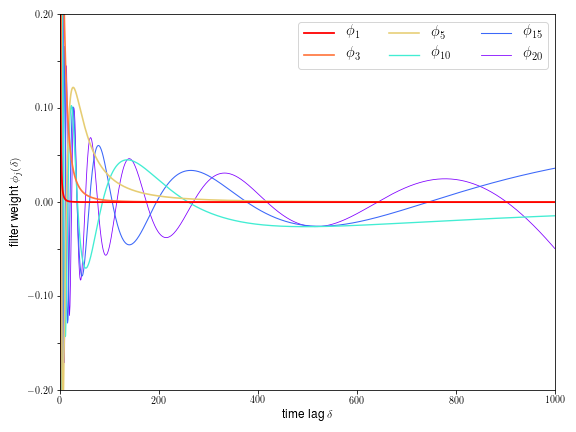
滤波器幅值与时间关系图中描绘的一组滤波器。借助频谱滤波技术，我们可以使用多个滤波器预测给定时间的线性动态系统状态。每个滤波器都是一组权重，用于总结过去的观察值，这样就可以以加权方式将它们组合起来，随着时间的推移，我们可以更准确地预测系统

这些权重（过滤器）的数学推导与汉克尔矩阵的频谱理论之间存在着有趣的联系。

展望未来

在与普林斯顿大学的师生合作过程中，我们的研究工作取得了诸多令人兴奋的进展，期待实验室在未来几周内正式投入使用。长期以来，Google 一直认为开放的研究文化对行业和学术界都大有裨益，我们期待继续开展紧密合作。

致谢

本文中讨论的研究和成果离不开下列研究人员的贡献：Naman Agarwal、Brian Bullins、Xinyi Chen、Udaya Ghai、Tomer Koren、Karan Singh、Cyril Zhang、Yi Zhang 和客座教授 Sham Kakade。自今年年初加入 Google 以来，该研究团队一直在 Google 纽约办公室和普林斯顿大学远程工作，他们有望在未来几周内搬进普林斯顿校园对面新的 Google 办公空间。

更多 AI 相关阅读：