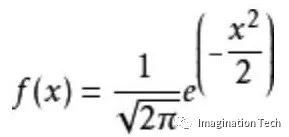【原理】学懂GAN的数学原理，让它不再神秘

知乎上有个讨论，说学数学的看不起搞深度学习的。曲直对错不论，他们看不起搞深度学习的原因很简单，因为从数学的角度看，深度学习仅仅是一个最优化问题而已。比如，被炒的很热的对抗式生成网络(GAN)，从数学看，基本原理很容易就能说明白，剩下的仅仅是需要计算资源去优化参数，是个体力活。

本文的目的就是尽可能简单地从数学角度解释清楚GAN的数学原理，看清它的庐山真面目。

1，从生成模型说起

机器学习的模型可分为生成模型和判别模型。

简单说说二者的区别，以二分类问题来讲，已知一个样本的特征为x，我们要去判断它的类别y(取值为0,1)。也就是要计算p(ylx)，假设我们已经有了N个样本。

计算p(ylx)的思路有两个，一个就是直接求，即y关于x的条件分布，逻辑回归就是这样干的。凡是按这种思路做的模型统一称作判别模型

另一个思路是曲线救国，先求出x,y的联合分布p(x,y)，然后，根据p(ylx)=p(x,y)/p(x)来计算p(ylx)，朴素贝叶斯就是这样干的。凡是按这种思路做的模型统一称作生成模型。

那么，GAN属于什么呢？答案是生成模型，因为它也是在模拟数据的分布。

举个例子，我们有N张尺寸为50*50的小猫的照片，先不管这些猫多可爱，多漂亮，从数学的角度看，一张猫的图片可以理解为2500维空间中的一个点或者说是一个2500维的向量，N张图就是N个点或者说向量。如果我们想让神经网络自动生成一个小猫的图片，所要做的就是假设N张图片都是某个2500维空间中的随机分布的样本，这个分布抽样产生的点就是一张猫的图片。

这里有一个问题，需要再思考一下，我们假设的这个分布存在吗？答案是存在的，因为这是GAN的理论基础，没有这个假设，GAN就玩不下去了。具体的证明过于数学了，此刻，我们只要相信它存在就是了。

假设图片背后隐藏的分布是Pd(d就是data)，我们的任务就是用神经网络生成一个分布Pg(g就是generate)，只要Pg和Pd很接近，就可以用Pg生成一张小猫的图片了。

2，GAN解决的基本问题

根据上面的讨论，我们要解决两个问题:

一是如何用神经网络构造一个模拟分布Pg，

另一个是如何衡量Pg和Pd是否相似，并根据衡量结果去优化Pg

这就是GAN解决的最根本的两个问题。

3，GAN是如何解决这两个问题的？

第一个问题很容易解决，以上面的小猫问题为例，只要做一个神经网络，它的输入是来自某个特定分布的数，为便于说明，我们就假设这个特定分布是一维的，也就是它产生的数就是一个标量，如1，2.5之类的，经过多层的映射后，产生一个2500维的向量。可以想象，只要输入来自一个特定的分布，映射产生的2500维向量也会形成一个分布。这个分布的概率密度函数就是输入分布的概率密度函数在2500维空间的扩展。

我们来举个例子，为了说明问题，这里假设神经网络映射后也是一个一维的数，不再是上面例子中的2500维向量，但我们要清楚，其原理是一样的。

假设我们的输入分布是一个标准正态分布，其概率密度函数为

标准正态分布

我们的神经网络就相当于一个函数y=g(x)，现在已知x的概率密度函数如上所示，那么y的概率密度函数会是什么样子呢？

没有什么是一个例子说明不了的，如果有，那就两个。

假设g就是一个等值映射，即g(x)=x，显然y与x的概率密度函数一样，也是标准正态分布。

如果g(x)=x+1，那么，y的概率密度函数就是均值为1，方差为1的正态分布。

可见，神经网络对某个特定分布x映射后的y确实是一个分布，其概率密度函数既与x的概率密度函数相关，又与神经网络的结构g函数相关。这里说的网络结构有两层含义，一个网络的内部构造，另一个就是网络的输出向量维数。我们虽然只举了输出为1维的情况，但在输出是多维时，y的分布会有一些新的特点。

比如，一个有趣的问题是，若原始的输入是一维的正态分布，其取值空间是整个一维实数空间，如果输出的是多维向量分布，那么，它的取值空间还会是整个多维空间吗？

这个问题让我联想到《三体》，太阳系遭受二向箔攻击后，变成了二维空间，逃离的人类，开始寻找更高级的宇宙文明，期望有一天，能够将二维化的地球还原成三维的世界。

第二个问题如何解决呢？

回到刚才小猫的问题，假设我们有一万个样本图片，也有了一个生成分布的神经网络G，它的输入是一个正态分布。输出是2500维的向量。

从数学上讲，我们的问题是，如何衡量Pd，Pg的相似性，以及如何使Pg接近Pd。

具体的方法不用我们费心想了，我们直接看现成的就可以。

即再定义一个NN，叫做D，D(x)产生的是0到1之间的一个值

定义函数

V(G, D) = Ex~Pd(log(D(x)) + Ex~Pg(log(1-D(x))

对于一个特定的G，通过调整D，可以得到maxV(G,D)，它就能衡量Pd和Pg的difference，这个值越小， 二者差距越小。

为什么maxV(G,D)可以衡量两个分布的差异？

我们先直接观察V，把D看作一个判别器，V的第一部分表示D对来自真实分布的数据的评分的期望，第二部分表示D对来自G生成的数据的评分与1的差的期望。

最大化V，就是要使D对来自真实数据的评分尽可能高，对来自G生成的数据的评分尽可能低(即让1-D(x)尽可能高)。

至此，我们看到，V越大，表示D对来自真实分布和来自G的数据评分差异越大，真实的样本越接近1，G产生的样本越接近0。

通过调整D，得到的maxV，表示在我们能力范围内，我们找到的最强的D，它能把Pd和Pg产生的数据区分开的程度。自然，这个区分程度就表示了Pd和Pg的差异程度。因为可以想象，Pd和Pg越接近，同样的D，得到的V肯定越小。因为二者产生的数据越难区分开。

以上，是通过直观的分析得出的一些认识，我们还可以从数学上进行一些分析。

对V做一些变形，可以得到如下

V = Σ（Pd*log(D(x)) + Pg*log(1-D(x))）

       x

maxV时，我们只要看对于一个x，如何最大化这个值即可：

Pd*log(D(x)) + Pg*log(1-D(x))

这里，除了D是变化的，其他都是已经给定的，

令a=Pd，D=D(x)， b = Pg

a，b都是一个确定的数值，因为x此时是确定的，上式进一步变成这样

alogD + blog(1-D)

对这个式子，求导，很容易得出最佳的D值是：

D^* = a/(a+b) 可见，D的值确实是0到1之间的值

再将D^*带入最上面的V的定义中，经过一系列的计算推导(此处省略了推导过程，感兴趣的小伙伴可以自己推导一下)，我们可以得出maxV实际表示的是Pd

和(Pd+Pg)/2的KL散度加上Pg和(Pd+Pg)/2的KL散度

如果令g = (Pd+Pg)/2，则

maxV = -2log2 + KL(Pd||g) + KL(Pg||g)

如果有小伙伴对KL散度不是很理解，推荐看看我的另一篇文章《机器学习面试之各种混乱的熵》，里面有一个很通俗易懂的解释。

这里有一个数学定义:

JSD(Pg||Pd)=1/2*(KL(Pd||g) + KL(Pg||g))

根据定义，maxV就变成这样了:

maxV = -2log2 + 2JSD(Pg||Pd)

JSD全称是Jessen-Sannon Divergence，它是一个对称化的KL散度。

从数学上可以证明，JSD最大值是log2，最小值是0

所以maxV最大值是0，最小值是-2log2。

至此，我们的第二个问题已经解决了一半，将Pd和Pg的差异量化成了一个-2log2到0之间的一个数值。

另一半问题就是如何针对求出的最大化V的D，更新调整G，使得maxV变小一点。

我们将maxV定义为L(G)，即

L(G)=maxV

可见，maxV实际上就是G的损失函数，可以用梯度下降更新神经网络G的各个参数得到G1，使得maxV下降。

有了G1后，我们再次重复上面的最大化V的过程，得到D1，然后再次运用梯度下降，得到G2，如此循环下去，可以期待，Pg将会越来越接近Pd。

上图来自李宏毅深度学习课程截图

这是从理论上证明的，如果你感觉看得比较晕乎，没关系，我们下面就来看看实践中的做法。

4，实践中的做法

以上的推导都是从理论上进行的分析，在工程实践中，有个问题必须解决:

我们并不能真正知道Pd，我们只是有很多Pd产生的样本，自然也求不出logD(x)关于Pd的期望，对于Pg的期望也有类似困难。

那么，实践中是怎么做的呢？

首先，既然直接计算期望而不可得，我们只能退而求其次，从Pd中sample 出m个样本，再从Pg中sample出m个样本，最大化D(x)在这2m个样本的V值，如下图所示：

仔细观察上式，最大化V的过程，就是将Pd产生的样本作为正样本，Pg产生的样本作为负样本，训练一个分类器D的过程。

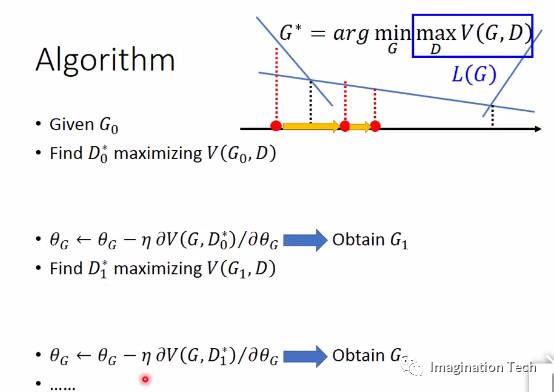
完整的算法如下所示：

该图同样来自李宏毅深度学习课程

另外，在工程实践中，还有一个实际的调整，就是将V蚯蚓中的log(1-D(x))改为-log(D(x))

原因是：

D的值在0到1之间，

在刚开始时，由于G生成的图像比较挫，D可以很容易分辨出来，也就是生成的值都远小于0.5，V蚯蚓关于G的参数θg的梯度等于 log(1-D(x))关于D的梯度再乘以D关于θg的梯度，但是此时，log(1-D(x))在0到0.5之间的梯度比较小，这就会导致θg的更新比较慢，但是换成-log(D(x))后，它在0到0.5之间的梯度是比较大的，可以快速的更新g的参数。这符合我们的直觉，就是一开始学习要快一点，后面要慢一点。

5，无总结，不进步

纵观整个GAN，本来我们要求Pg和Pd之间的相似度，由于不能直接求，转而借助一个D，maxV求出一个最佳的D后，maxV就是在衡量Pg和Pd的JS 散度，然后，最小化这个散度值，更新一次Pg，有了新的Pg后，进一步求出最佳的D，然后重复上面的步骤。

作者：milter
來源：简书(http://www.jianshu.com/p/5842ca632816)

高质量延伸阅读

☞  【最详尽的GAN介绍】王飞跃等：生成式对抗网络 GAN 的研究进展与展望

☞  【智能自动化学科前沿讲习班第1期】王飞跃教授：生成式对抗网络GAN的研究进展与展望

☞  【智能自动化学科前沿讲习班第1期】王坤峰副研究员：GAN与平行视觉

☞  【重磅】平行将成为一种常态：从SimGAN获得CVPR 2017最佳论文奖说起

☞  【平行讲坛】平行图像：图像生成的一个新型理论框架

☞  【计算机视觉简介】历史、现状和发展趋势

☞  【CMU与FAIR】联合发布非局部神经网络，有效提升视频分类、对象分割、姿态估计结果

☞ .【最新前沿】Facebook何恺明等大神最新论文提出非局部神经网络（Non-local Neural Networks）

☞  【Ian Goodfellow盛赞】一个GAN生成ImageNet全部1000类物体

☞  【理论】究竟深度学习在干什么？