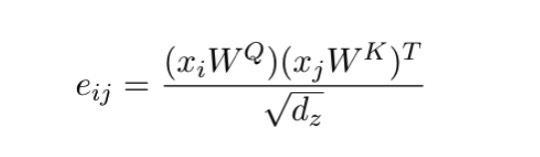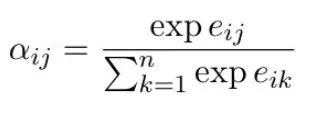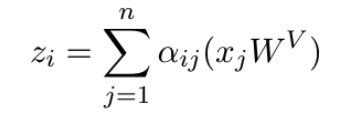自注意力机制和全连接的图卷积网络(GCN)有什么区别联系？

2020 年 7 月 11 日 极市平台

加入极市专业CV交流群，与 10000+来自港科大、北大、清华、中科院、CMU、腾讯、百度等名校名企视觉开发者互动交流！

同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总，行业技术交流。关注 极市平台 公众号，回复 加群，立刻申请入群~

本文整理自知乎问答，仅用于学术分享，著作权归作者所有。如有侵权，请联系后台作删文处理。

观点一

作者｜Guohao Li

https://www.zhihu.com/question/366088445/answer/1023290162

来说一下自己的理解。

首先结论是大部分GCN和Self-attention都属于Message Passing（消息传递）。GCN中的Message从节点的邻居节点传播来，Self-attention的Message从Query的Key-Value传播来。

Message Passing[4]

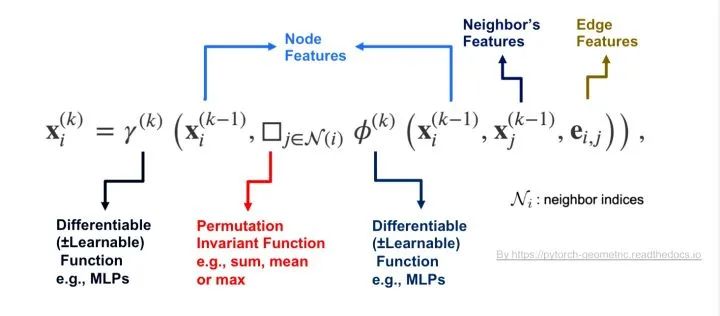
先看看什么是Message Passing。我们知道在实现和设计GCN的时候很多时候都是采用Message Passing的框架[3]，其思想是把每个节点的领域的特征信息传递到节点上。在这里举例描述一个节点i在第k层GCN卷积的过程：

1）把节点i的每一个邻居j与该节点的特征经过函数变换后形成一条Message（对应公示里函数\phi里面的操作）；

2）经过一个Permutation Invariant（置换不变性）函数把该节点领域的所有Message聚合在一起（对应函数\square）；

3）再经过函数\gamma把聚合的领域信息和节点特征做一次函数变化，得到该节点在第k层图卷积后的特征X_i。

那么Self-attention是否也落在Message Passing的框架内呢？我们先回顾一下Self-attention一般是怎么计算的[2]，这里举例一个Query i的经过attention的计算过程：

1】Query i的特征x_i会和每一个Key j的特征计算一个相似度e_ij；

2】得到Query i与所有Key的相似度后经过SoftMax得到Attention coefficient（注意力系数）\alpha_ij；

3】通过Attention coefficient加权Value j计算出Query i最后的输出z_j。

好了，那么我们来看看它们之间的对应关系。首先结论是Self-attention计算中的1】2】3】是对应Message Passing里的1）2）的。

如果用Message Passing来实现Self-attention，那么我们可以这么一一对应：

-1 每个Key-Value j可以看作是Query i的邻居；

-2 相似度和注意力系数的计算和最后3】中Value j与注意力系数相乘的操作可以对应为Message Passing中第一步构成Message的过程；

-3 最后Self-attention的求和运算对应Message Passing中第二步的Permutation Invariant函数，也就是说这里聚合领域信息的过程是通过Query对Key-Value聚合而来。

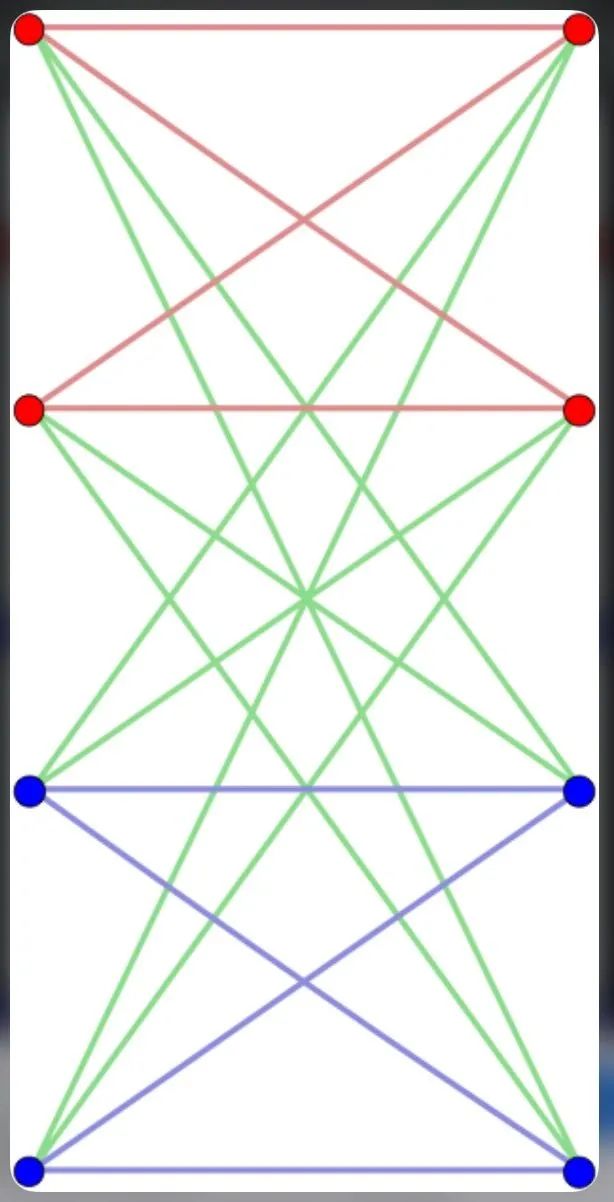
那么也就是说，Attention的过程是把每一个Query和所有Key相连得到一个Complete Bipartite Graph（左边是Query右边的Key-Value），然后在这图上去对所有Query节点做Message Passing。当然Query和Key-Value一样的Self-attention就是在一般的Complete Graph上做Message Passing了。

Complete Bipartite Graph

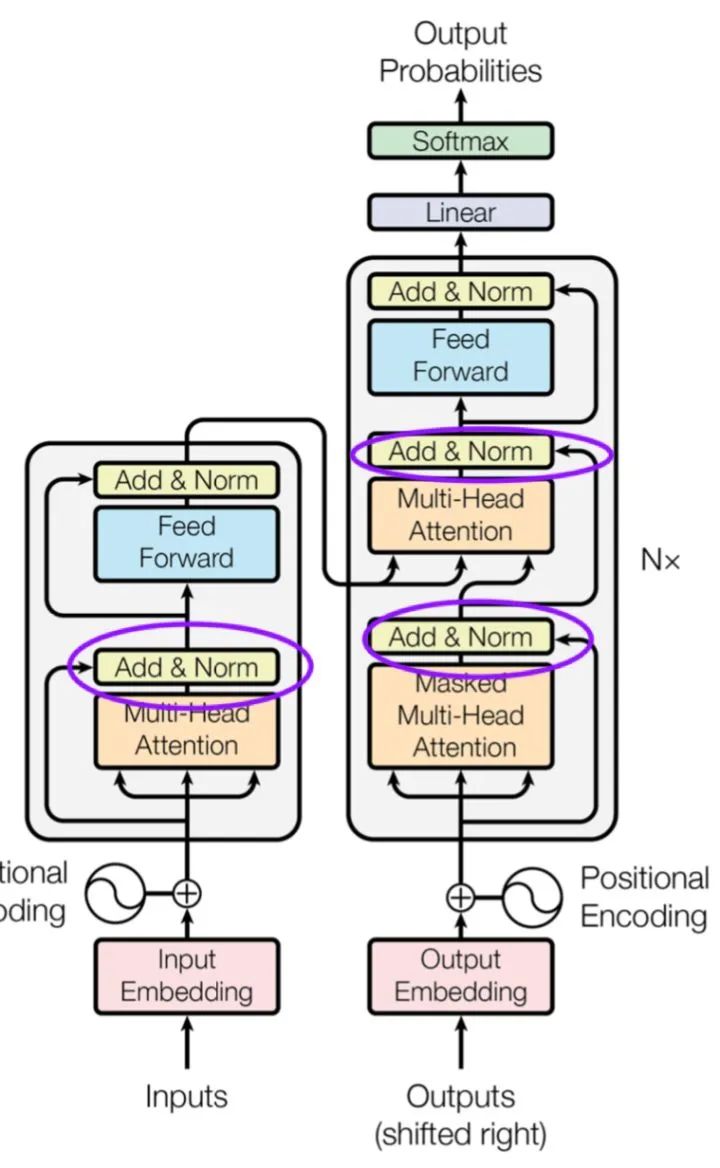
看到这里大家可能疑问那么为什么Self attention里面没有了Message Passing中第三步把聚合的信息和节点信息经过\gamma函数做变换的过程呢。是的，如果没有了这一步很可能学习过程中Query的原来特征会丢失，其实这一步在Attention is all your need[1]里还是有的，不信你看：

在每一次经过Self-Attention之后基本上都是有Skip connection+MLP的，这里某种程度上对应了Message Passing里的\gamma函数不是吗？

那么说白了GCN和Self-attention都落在Message Passing（消息传递）框架里。GCN中的Message从节点的邻居节点传播来，Self-attention的Message从Query的Key-Value传播来。如果称所有的Message Passing函数都是GCN的话，那么Self-attention也就是GCN作用Query和Key-Value所构成Complete Garph上的一种特例。也正如乃岩 @Naiyan Wang的回答一样。

可以说NLP中GCN应该大有可为，毕竟Self-attention可以看出是GCN一种，那么肯定存在比Self-attention表达能力更强和适用范围更广的GCN。

感谢评论里 @叶子豪的补充，DGL团队写了个很详尽的用Message Passing实现Transformer的教程。对具体实现感兴趣的同学可以去读一下：DGL Transformer Tutorial。

Reference：

1. Attention is All You Need

2. Self-Attention with Relative Position Representations

3. Pytorch Geometric

4. DeepGCNs for Representation Learning on Graphs

观点二

作者｜Houye

https://www.zhihu.com/question/366088445/answer/1022692208

来说一下自己的理解。

GAT中的Attention就是self-attention，作者在论文中已经说了

下面说说个人理解：

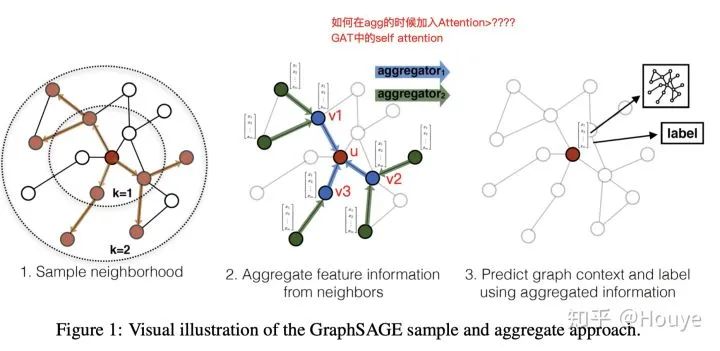
GNN，包括GCN，是一种聚合邻居信息来更新节点表示的神经网络模型。下图取自GraphSAGE，感觉比较好的说明了聚合过程。这里我们只关注图2：红色的点u是我们最终需要关注的点，3个蓝色的点{v1,v2,v3}是红色点的一阶邻居。每次更新在红色节点表示的时候，GNN都会收集3个蓝色点的信息并将其聚合，然后通过神经网络来更新红色节点的表示。这里神经网络可以是一个mean-pooling，也是对邻居进行平均，这时候 v1，v2，v3的权重都是1/3。

那这里就有问题了，3个蓝色的点都是邻居，直观的想，不同邻居对于红色的点的重要性是不同的。那么，在GNN聚合邻居的时候能不能考虑到邻居的重要性来加权聚合呢（比如，0.8v1+0.19v2+0.01v3）？手动加权肯定是不实际的。虽然加权感觉好一些，但是不加权也是可以做GNN的，在有些数据集上，不加权的效果甚至更好。

个人感觉在深度学习领域，“加权=attention”。我们这里可以设计一种attention机制来实现对邻居的加权。这里的权重可以理解为边的权重，是针对于一对节点来说的（比如u和v1）.

那这里为啥是self-attention，因为GNN在聚合的时候会把自身也当做邻居。也就是说，上图中u的邻居集合实际是{u,v1,v2,v3}。这是很自然的，邻居的信息只能算是补充信息，节点自身的信息才是最重要的。

现在问题转化成了：给定{u,v1,v2,v3}作为输入，如何将u更好的表示出来？这个就很像NLP里面的self-attention了，见下图（引自川陀学者：Attention机制详解（二）——Self-Attention与Transformer）