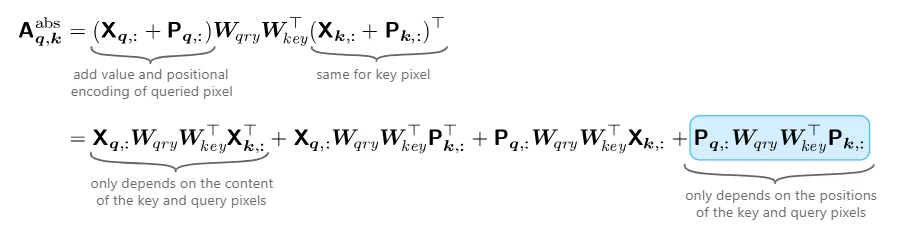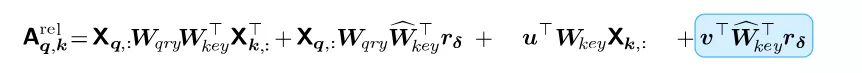无所不能的Self-Attention！洛桑理工ICLR2020论文验证「自注意力可以表达任何CNN卷积滤波层」

【导读】自注意力机制Self-attention近年来在深度学习方法中得到了广泛的应用，围绕self-attention的transformer模型已经在自然语言处理中成为基础模型构件，能够建模序列模型RNN/LSTM的作用，并且能够并行化。但是与卷积神经网络相比，self-attention能否建模达到同样的作用？最近，来自瑞士联邦理工学院在ICLR2020的论文验证了self-attention与卷积层的关系《On the Relationship between Self-Attention and Convolutional Layers 》，表明一个自注意力层可以表达任何卷积滤波器，只要有足够的头和使用相对位置编码。

Self-attention对文本处理产生了很大的影响，并成为自然语言理解NLU的不可缺少的构建模块。但是这种成功并不局限于文本(或者一维序列)——基于transformer的架构可以在视觉任务上打败最先进的ResNet技术[1,2]。为了解释这一成果，我们的工作[3]表明，self-attention可以表达CNN层，这种卷积滤波层是在实际任务中得到。我们提供了一个互动网站来探索我们的结果。

图1: 9个头的一个查询像素(黑色中心正方形)的注意力得分(单独标绘)。如果在每个查询像素上，每个注意力头都能在任意的移动中注意到单个像素(红色)会怎么样?然后，自注意层可以表示一个大小为3×3的卷积滤波器……我们证明了多头自注意层有能力表现这种模式，并且这种行为是在实际中学习得的。多头自注意是卷积层次的泛化。

Ashish Vaswani和同事[4]引入的transformer架构已经成为自然语言理解的主要工具。transformer与以往的方法，如递归神经网络(RNN)和卷积神经网络(CNN)的关键区别在于transformer可以同时处理输入序列中的每一个单词。

自注意力与卷积层 Self-Attention & Convolutional Layers

为了指出卷积层和自注意力层之间的相似点和不同点，我们首先回忆一下它们是如何处理形状为W×H×D的图像的。CNNs背后的机制是很容易理解的，但是将transformer架构从1D(文本)提升到2D(图像)需要很好地掌握自注意力机制。你可以参考所有你需要的Attention is All You Need[4]的论文和Transformer的博客文章The Illustrated Transformer来解释1D的情况。

卷积层 Convolutional Layer 卷积神经网络(CNN)由许多卷积层和子采样层组成。每个卷积层学习大小为K×K的卷积滤波器，输入和输出维度分别为Din和Dout。该层的参数化是四维核张量W位数为 K×K×Din×Dout和维数为Dout的偏差向量b进行的。

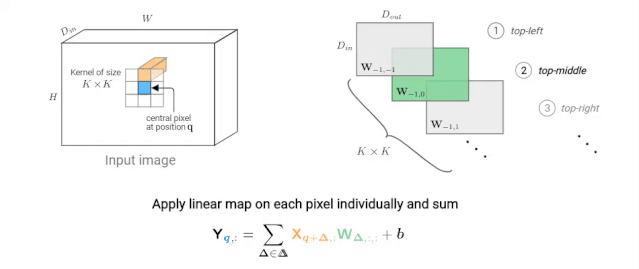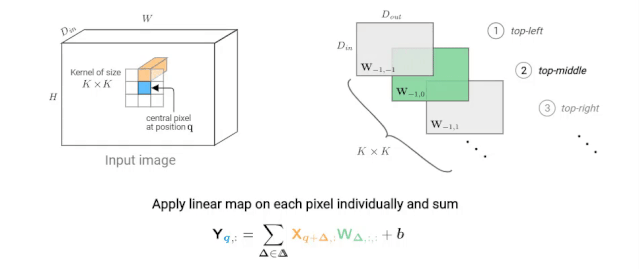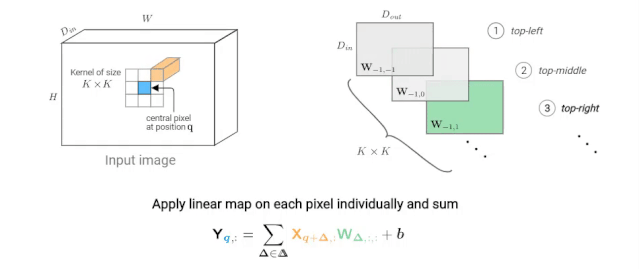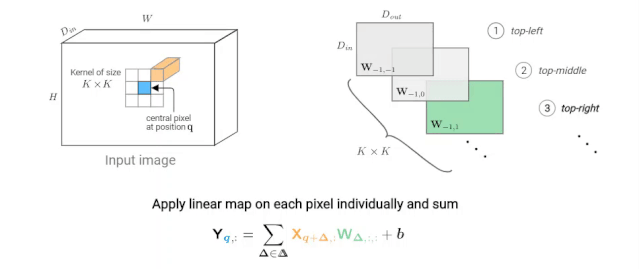
下图描述了如何计算像素q的输出值。在动画中，我们独立考虑每个核跳跃shift，这种观点可能不太常用，但在下面我们比较卷积和自注意力层时，它将被证明是有用的。

图2: K×K卷积在给定像素(蓝色)处的输出值的计算示意图。

多头自注意力层 Multi-Head Self-Attention Layer CNN和self-attention layers之间的主要区别是一个像素的新值依赖于图像的其他像素。与接受域为 K×K邻域网格的卷积层不同，自注意力的感受野总是全图。这带来了一些缩放的挑战，当我们应用Transformer到图像，我们没有覆盖在这里。现在，让我们定义什么是多头自注意力层。

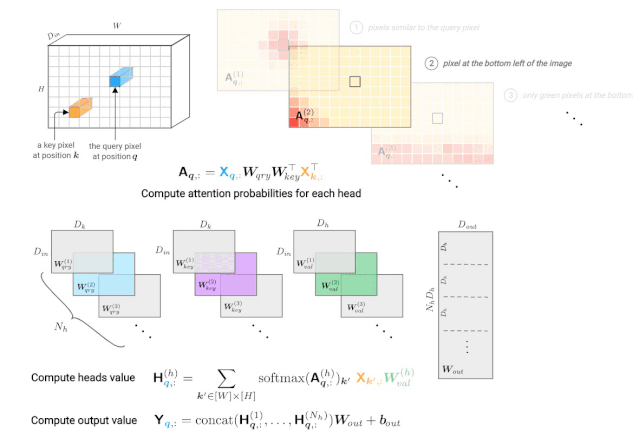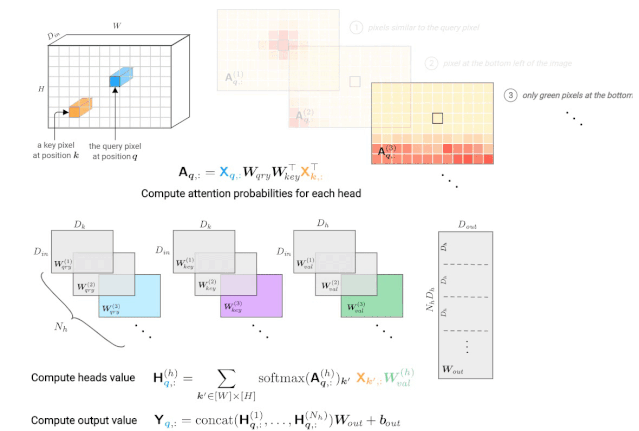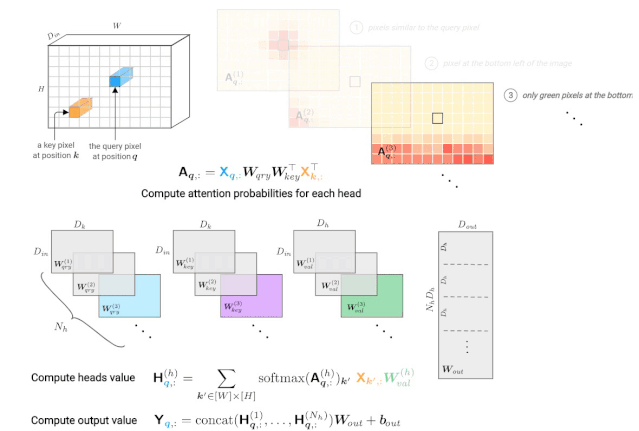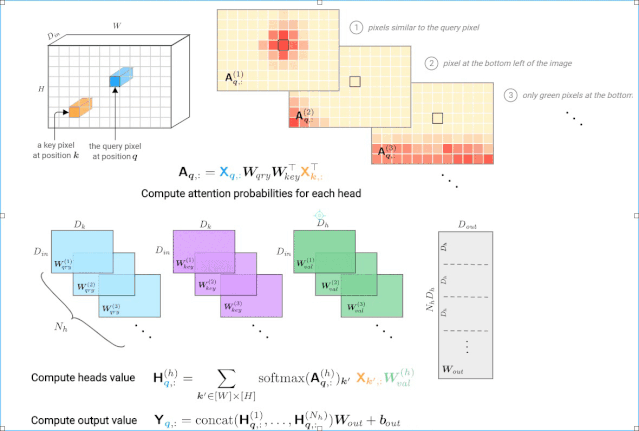
图3: 由一个多头自注意力层计算一个查询像素(深蓝色)的输出值。右上角显示每个头部的注意概率示例，红色位置表示“注意力中心”。

注意概率的计算基于输入值X。这个张量经常用位置编码来增广(通过加法或拼接)，从而使图像中的像素位置之间的距离扩大。注意能力模式的假设例子说明了对像素值和/或位置的依赖关系: 1. 使用查询的值和键像素，2. 只使用关键像素的位置编码，3. 使用关键像素的值及其位置。

再参数化 Reparametrization

你可能已经看到了自我注意力和卷积层之间的相似性。

定理：

自注意力层表达卷积的两个最关键的要求是:

有多个头去处理卷积层感受野的每个像素，

使用相对位置编码来确保翻译的方差相等。

第一点可以解释为什么多头注意力比单头注意力更有效。关于第二点，我们接下来给出了关于如何编码位置以确保自我注意可以计算卷积的见解。

相对位置编码 Relative Positional Encoding

上面描述的自注意力模型的一个关键特性是，它与重排序是等价的，也就是说，它给出的输出与输入像素的打乱方式无关。对于我们期望输入顺序重要的情况，这是有问题的。为了减轻这种限制，对序列中的每个标记(或图像中的像素)进行位置编码，并在应用自注意力机制之前将其添加到标记本身的表示中。

注意概率(图3，右上角)是根据输入值和层输入的位置编码计算的。我们已经看到，对于每个查询像素，每个头部可以聚焦在图像的不同部分(位置或内容)。我们可以明确地分解这些不同的依赖关系如下:

因为卷积层的感受野不依赖于输入数据，所以只需要最后一项就可以实现自我注意力对CNN表现。

我们所忽略的CNN的一个重要特性是翻译的等方差。这可以通过用相对位置编码代替绝对位置编码来实现 这种编码最早是由Zihang Dai和他的同事在TransformerXL[5]提出的。主要的思想是只考虑位置差异δ= k−q之间的关键(像素参加)和查询像素(像素计算)的表示而不是绝对位置的像素的关键。The absolution attention概率可以用一种相对的方式重写：

在这种情况下，注意力得分只取决于移动，我们实现了平移等方差。最后,我们表明,存在一组的相对位置向量维度Dpos = 3以及self-attention参数允许参加像素在任意转移(图1)。我们认为任何卷积过滤器可以由多头self-attention在满足在上面的定理条件下进行表达。

学习注意力模式 Learned Attention Patterns

尽管我们证明了自注意力层有能力表达任何卷积层，但这并不一定意味着这种行为会在实际中可以发挥作用。为了验证我们的假设，我们实现了一个6层的全注意力模型，每层有9个头部。我们在CIFAR-10上训练了一个监督分类目标，并达到了94%的良好准确率(虽然不是最先进的，但已经足够好了)。我们重新使用了从Irawn Bello和同事[1]那里学到的相对位置编码，分别学习了行偏移和列偏移编码。主要的区别是我们只使用相对位置来设定注意概率，而不是输入值。

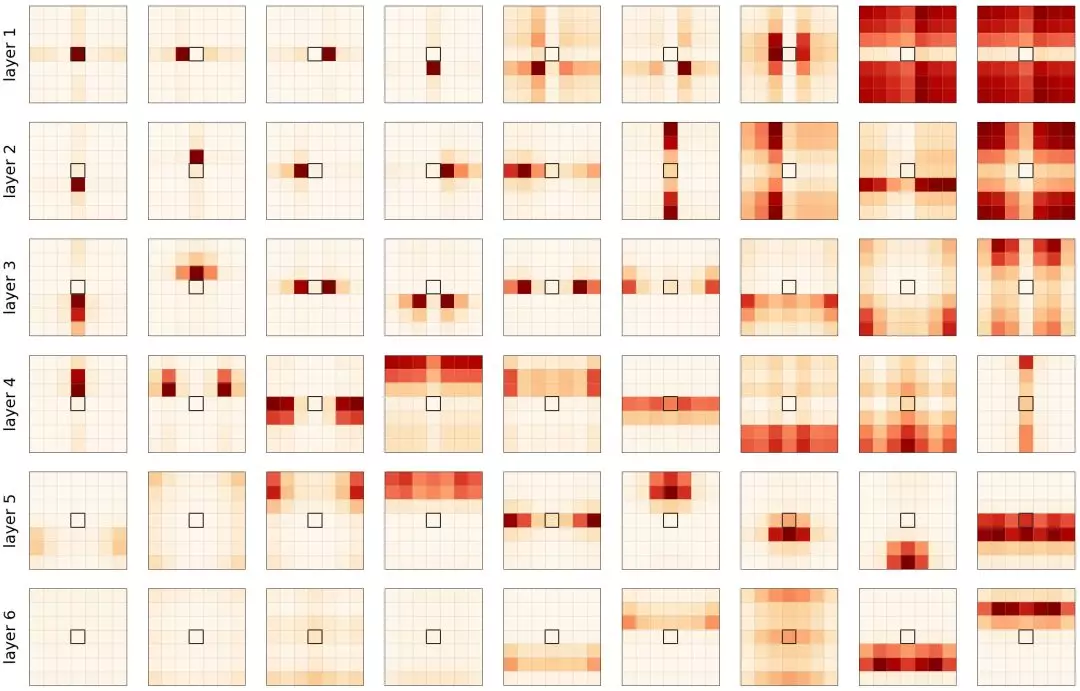
图4所示的注意力概率表明，确实，自注意力的行为与卷积相似。每个头部都学会关注图像的不同部分，重要的注意力概率通常都是局部的。

图4: 使用学习的相对位置编码在每个层(行)上的每个头(列)的注意映射。中间的黑色方块是查询像素。我们重新排列了头部以使其可视化。

我们还可以观察到，第一层(1-3)专注于非常接近和特定的像素，而较深层(4-6)专注于图像整个区域的像素的更多全局斑块。在这篇论文中，我们进一步用更多的头做实验，观察到比网格像素更复杂的(学习到的)模式。

结论 Conclusion

在我们关于卷积层和自注意力之间关系的论文[3]中，我们证明了一个自注意力层可以表达任何卷积滤波器，只要有足够的头和使用相对位置编码。这可能是为什么需要多个头的第一个解释。事实上，多头自注意力层概括了卷积层: 它学习整个图像上感受野的位置(而不是一个固定的网格)。感受野甚至可以根据输入像素的值进行调整，我们将这个有趣的特性留到以后的工作中。希望我们关于图像位置编码的发现也能对文本有帮助，似乎使用2维的相对位置编码就足够了，但我们需要在实践中验证这一点。

参考文献：

Attention Augmented Convolutional Networks  [PDF] Bello, I., Zoph, B., Vaswani, A., Shlens, J. and Le, Q.V., 2019. CoRR, Vol abs/1904.09925.

Stand-Alone Self-Attention in Vision Models  [PDF] Ramachandran, P., Parmar, N., Vaswani, A., Bello, I., Levskaya, A. and Shlens, J., 2019. CoRR, Vol abs/1906.05909.

On the Relationship between Self-Attention and Convolutional Layers  [link] Cordonnier, J., Loukas, A. and Jaggi, M., 2020. International Conference on Learning Representations.

Attention is All you Need  [link] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, L. and Polosukhin, I., 2017. Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, 4-9 December 2017, Long Beach, CA, USA, pp. 5998--6008.

Transformer-XL: Attentive Language Models beyond a Fixed-Length Context  [link] Dai, Z., Yang, Z., Yang, Y., Carbonell, J.G., Le, Q.V. and Salakhutdinov, R., 2019. Proceedings of the 57th Conference of the Association for Computational Linguistics, ACL 2019, Florence, Italy, July 28- August 2, 2019, Volume 1: Long Papers, pp. 2978--2988.