Jürgen Schmidhuber：无监督神经网络在极大极小上的博弈

来源：Jürgen

编译：Bot

编者按：如果说GAN的发展史上有什么戏剧性事件，那“LSTM之父”Jürgen Schmidhuber（发音：You_again Shmidhoobuh）和“GAN之父”Ian Goodfellow之间的恩怨绝对是其中最精彩的一幕。在2016的NIPS大会上，Schmidhuber和Goodfellow就GAN是否借鉴了前者在九十年代发表的一篇论文展开了激烈争论，引得满座震惊。虽然事后学界认可了GAN的原创性，但Schmidhuber似乎对此仍然耿耿于怀。近日，他发表了一篇小短文，文章的主角还是几十年前的那个模型——PM。

1990s，无监督神经网络在最小值上的博弈 每个网络最小化由另一个网络最大化的值函数 或生成实验，产生对好奇心的内在奖励

在对人工神经网络（NN）的研究中，研究人员最重要的目标之一是创建能从给定数据中学习统计数据的算法。为了实现这一目标，我在20世纪90年代曾引入一种新型无监督学习机制，它基于极大极小博弈中的梯度下降/上升原理，其中一个NN负责最小化由另一个NN最大化的目标函数。我把发生在这两个无监督神经网络之间的对抗称为“可预测性最小化”（Predictability Minimization）。

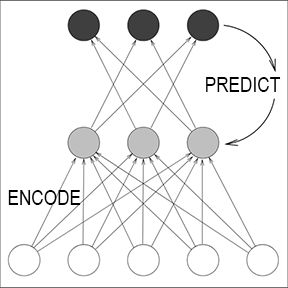
首先，PM需要一个自带初始随机权重的编码器网络，它通过其输入节点（下图中的白色圆圈）接收数据样本（例如图像），并在其输出节点（下图中的灰色圆圈，也称编码节点）生成对应编码。每个编码节点都可以在区间[0,1]内被激活。

图中的黑色圆圈表示一个独立的预测网络，经过训练后，给定一部分编码节点，它能学习每个编码节点的条件期望，从而预测所有未提供的编码节点。虽然图中没有标出，编码网络和预测网络都有隐藏节点。

但是，每个编码节点都希望自己能变得更不可预测。因此它需要经过训练，最大限度地提高由预测网络最小化的目标函数（如均方误差）。预测器和编码器相互对抗，以激励编码器实现无监督学习的“圣杯”——关于输入数据的理想的、展开的、二元的阶乘编码，其中每个编码节点在统计上彼此互相独立。

理想情况下，NN在经过学习后，给定数据模式的概率就应该等于其编码节点概率的乘积，这个概率也是预测网络的输出。

无独有偶，生成对抗网络（GAN）也使用无监督的极小极大原理来模拟给定数据的统计数据。相信读者都熟悉NIPS 2014的那篇GAN论文，虽然那位作者声称PM并不是基于值函数的极大极小博弈，不是一个网络寻求最大化而另一个寻求最小化，相比GAN那种“网络之间的对抗是唯一训练标准，并且足以完成训练”的方法，PM只能算“一个正则，鼓励神经网络的隐藏节点在完成其他任务时在统计上独立，其对抗性不是主要的训练方法”。

但是，我觉得PM确实也是个纯粹的极大极小博弈，尤其是它也对抗训练，“网络之间的对抗是唯一训练标准，并且足以完成训练”。

将无监督极大极小博弈用于强化学习好奇心

还是20世纪90年代，PM论文发表后，我曾尝试过把这个想法扩展到强化学习领域，构建具有人工好奇心的智能体。

我构建了一个目标是在环境中生成动作序列的神经网络C，它的动作生成的由一个追求回报最大化的节点控制。作为参考，我设计了一个名叫世界模型M的独立神经网络，它能根据给定的以往输入和动作预测未来输入。动作选择越合理，网络得到的回报就越高，因此C所获得的内在回报和M的预测误差成正比。同时，因为C试图最大化的正是M试图最小化的值函数，这意味着C会尽力探索M无法准确预测的新动作。

最近关于好奇心的强化学习论文有很多，我觉得它们都是基于这个简单的90年代的原理。尤其是在97年的那篇论文中[UARL3-5]，我让两个对抗的、追求回报最大化的模块（左脑和右脑）共同设计一个实验：一个能定义如何在环境中执行动作序列、如何通过实现由实验触发的观察序列的可计算函数（如二元分类）的指令序列来计算最终实验结果的（概率）程序。

两个模块都能提前预测实验结果，如果它们的预测或假设不同，那么在动作生成和执行完毕后，失败一方会向这个零和博弈的优胜一方提供内在回报。这种设计促使无监督的两个模块专注于“有趣”的事情，也就是不可预测的空间。同样的，在没有外部回报的情况下，每个无监督模块都在试图最大化由另一个最小化的值函数。

当时我在论文中提出，如果想把这种方法用于现实世界的某些问题，我们还需要科学家和艺术家的人为介入，设置合理的外部回报。而时至今日，很多人也确实正在用它处理数据分布建模和人工好奇心等任务。

小结

看到这里，相信大家都看出来了，Jürgen Schmidhuber还是放不下对GAN的纠结，或者说，是对“对抗”这种方法的执念。虽然GAN的原创性已无争议，但比起抬高/贬低Schmidhuber的为人，我们都不能否认他对深度学习作出的杰出贡献。2年前，他也正是以一种几乎“闹剧”的方式警告所有人，在过去几十年的研究中，可能存放着许多不为人知的珍宝，它们不是不够优秀，而只是输给了时代。

正如网友评价的：

作为机器学习的英雄，我们追随他；作为超越时代的罪人，我们围攻他。但他都可以接受，因为他不是英雄。他只是一个沉默的守护者，一个警惕的保护者，一个Schmidhuber。

参考文献

[PM1] J. Schmidhuber. Learning factorial codes by predictability minimization. Neural Computation, 4(6):863-879, 1992. Based on TR CU-CS-565-91, Univ. Colorado at Boulder, 1991. PDF. More.

[PM2] J. Schmidhuber. Netzwerkarchitekturen, Zielfunktionen und Kettenregel (Network architectures, objective functions, and chain rule). Habilitation (postdoctoral thesis), Institut for informatics, Tech Univ. Munich, 1993. PDF. HTML.

[PM3] J. Schmidhuber, M. Eldracher, B. Foltin. Semilinear predictability minimzation produces well-known feature detectors. Neural Computation, 8(4):773-786, 1996. PDF. More.

[PM4] N. N. Schraudolph, M. Eldracher, J. Schmidhuber. Processing Images by Semi-Linear Predictability Minimization. Network, 10(2): 133-169, 1999. PDF.

[PM5] P. Dayan, R. Zemel, and A. Pouget, 1992. Personal Communication. See [PM2], Sec. 6.9.3.

[ZIF] J. Schmidhuber. Neural predictors for detecting and removing redundant information. In H. Cruse, J. Dean, and H. Ritter, editors, Adaptive Behavior and Learning. Kluwer, 1998. PDF. HTML.

[GAN1] I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, Y. Bengio. Generative adversarial nets. NIPS 2014, 2672-2680, Dec 2014.

[PhD] J. Schmidhuber. Dynamische neuronale Netze und das fundamentale raumzeitliche Lernproblem (Dynamic neural nets and the fundamental spatio-temporal credit assignment problem). Dissertation, TUM, 1990. PDF. HTML.

[UARL1] J. Schmidhuber. Making the world differentiable: On using fully recurrent self-supervised neural networks for dynamic reinforcement learning and planning in non-stationary environments. Technical Report FKI-126-90, TUM, Feb 1990, revised Nov 1990. PDF

[UARL2] J. Schmidhuber. A possibility for implementing curiosity and boredom in model-building neural controllers. In J. A. Meyer and S. W. Wilson, editors, Proc. of the International Conference on Simulation of Adaptive Behavior: From Animals to Animats, pages 222-227. MIT Press/Bradford Books, 1991. PDF. HTML.

[UARL3] J. Schmidhuber. What's interesting? Technical Report IDSIA-35-97, IDSIA, July 1997. More on artificial curiosity.

[UARL4] J. Schmidhuber. Artificial Curiosity Based on Discovering Novel Algorithmic Predictability Through Coevolution. In Proc. CEC 1999, p. 1612-1618, IEEE Press, Piscataway, NJ, 1999.

[UARL5] J. Schmidhuber. Exploring the Predictable. In Ghosh, S. Tsutsui, eds., Advances in Evolutionary Computing, p. 579-612, Springer, 2002. PDF. HTML.

[AC91b] J. Schmidhuber. Adaptive curiosity and adaptive confidence. Technical Report FKI-149-91, Institut fuer Informatik, Technische Universitaet Muenchen, April 1991. PDF.

[AC91] J. Schmidhuber. Curious model-building control systems. In Proc. International Joint Conference on Neural Networks, Singapore, volume 2, pages 1458-1463. IEEE, 1991. PDF. HTML. Numerous papers on artificial curiosity followed later.

[AC09] J. Schmidhuber. Art & science as by-products of the search for novel patterns, or data compressible in unknown yet learnable ways. In M. Botta (ed.), Et al. Edizioni, 2009, pp. 98-112. PDF. (More on artificial scientists and artists.)

[ICML18ws] J. Schmidhuber. Unsupervised Minimax: Nets That Fight Each Other. Slides for the ICML 2018 Workshop on Theoretical Foundations and Applications of Deep Generative Models. PDF.