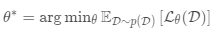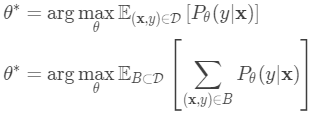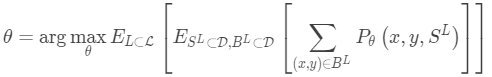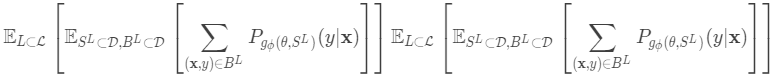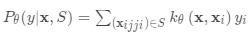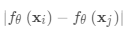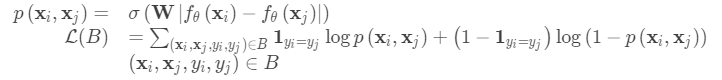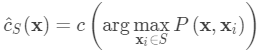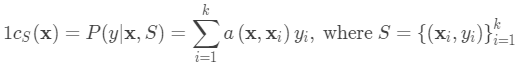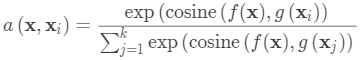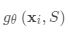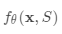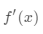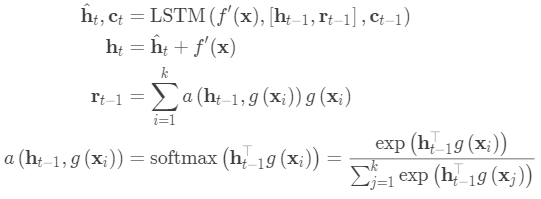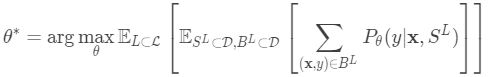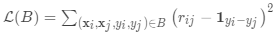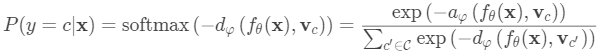Meta-Learning 元学习:学会快速学习
【导读】元学习,也称为“学习学习”,旨在通过一些训练少量样本可以学习新技能或快速适应新环境的模型。有三种常见的方法:1)学习有效的距离度量(基于度量); 2)使用(循环)网络与外部或内部存储器(基于模型); 3)明确优化模型参数以进行快速学习(基于优化)。
良好的机器学习模型通常需要使用大量样本进行训练。相比之下,人类能够更快,更有效地学习新的概念和技能。只看过几次猫和鸟的孩子可以很快分辨它们;会骑自行车的人很快就能上手摩托车。是否有可能通过一些训练少量样本快速设计出具有类似属性的机器学习模型?这就是元学习旨在解决的问题。
一个良好的元学习模型能够很好地推广到在训练期间从未遇到过的新任务和新环境。最终,改编的模型可以完成新任务。这就是元学习也被称为学习如何学习学习的原因。
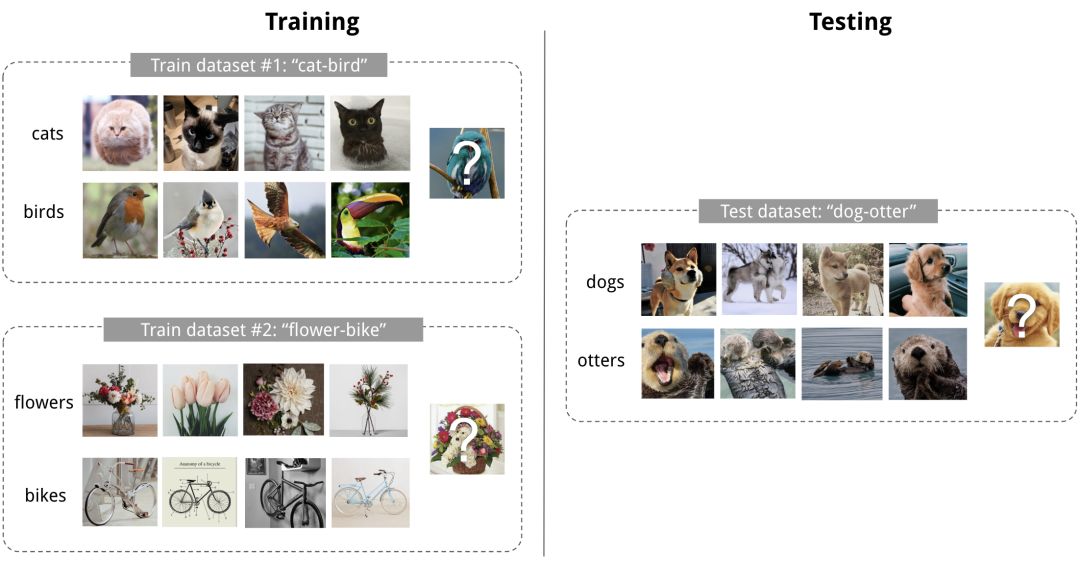
任务可以是任何明确定义的机器学习问题系列:监督学习,强化学习等。例如,这里有几个具体的元学习任务:
本文将分为两部分,第一部分主要介绍元学习的定义和基于度量的元学习,第二部分介绍基于模型和基于优化的元学习,尽情期待!
元学习问题的定义
一个简单的视角
一个好的元学习模型应该在各种学习任务上进行训练,并针对任务进行优化。 每个任务都与数据集相关联,数据集包含特征向量和真实标签。 最佳模型参数是:
它看起来与正常学习任务非常相似,但是一个数据集被视为一个数据样本。
Few-shot classification是监督学习领域中元学习的实例。 数据集通常被分成两部分,一个用于学习的支持集\和一个用于训练或测试的预测集,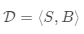
数据集包含特征向量和标签对,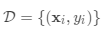
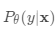
最佳参数应最大化真实标签的概率
在Few-shot classification中,目标是给定“快速学习”的小数据集,减少预测误差。 我们希望使用标签子集“伪造”数据集,以避免将所有标签暴露给模型并相应地修改优化过程以鼓励快速学习:
对标签子集进行采样。
对支持集和训练batch进行采样。 它们都只包含带有属于采样标签集的标签的数据点。
支持集是模型输入的一部分。
最终的优化使用小批量计算损失并通过反向传播更新模型参数,就像在监督学习中一样。
每对采样数据集可以视为一个数据点。 完成对模型训练之后,它可以推广到其他数据集。
该想法在某种程度上类似于仅有一组特定数据样本可用时,在图像分类(ImageNet)或语言建模(大文本语料库)中使用预训练模型。 元学习将这一想法更进一步,但是它不是根据一个下行任务进行微调,而是靠优化模型。
Learner和Meta-Learner
元学习的另一种流行观点将模型更新分解为两个阶段:
分类器 是训练用于操作给定任务的“学习者”模型; 与此同时,优化器gφ学习如何通过支持集更新学习者模型的参数
然后在最后的优化步骤中,我们需要更新θ和φ以最大化
常见方法
元学习有三种常用方法:基于度量,基于模型和基于优化。 Oriol Vinyals在他NIPS 2018的演讲中有一个很好的总结:
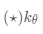
接下来我们将回顾每种方法中的经典模型。
基于度量的元学习
基于度量的元学习中的核心思想类似于最近邻算法(即,k-NN分类器和k均值聚类)和核密度估计。 一组已知标签
上的预测概率是支持集样本的标签的加权和。 权重由核函数
生成,测量两个数据样本之间的相似性。
学习一个好的内核对于基于度量的元学习模型的成功至关重要。度量学习与此意图完全一致,因为它旨在学习对象的度量或距离函数。良好指标的概念取决于问题。它应该代表任务空间中输入之间的关系,并促进解决问题。
下面介绍的所有模型都明确地学习了输入数据的嵌入向量,并使用它们来设计适当的核函数。
卷积Siamese神经网络
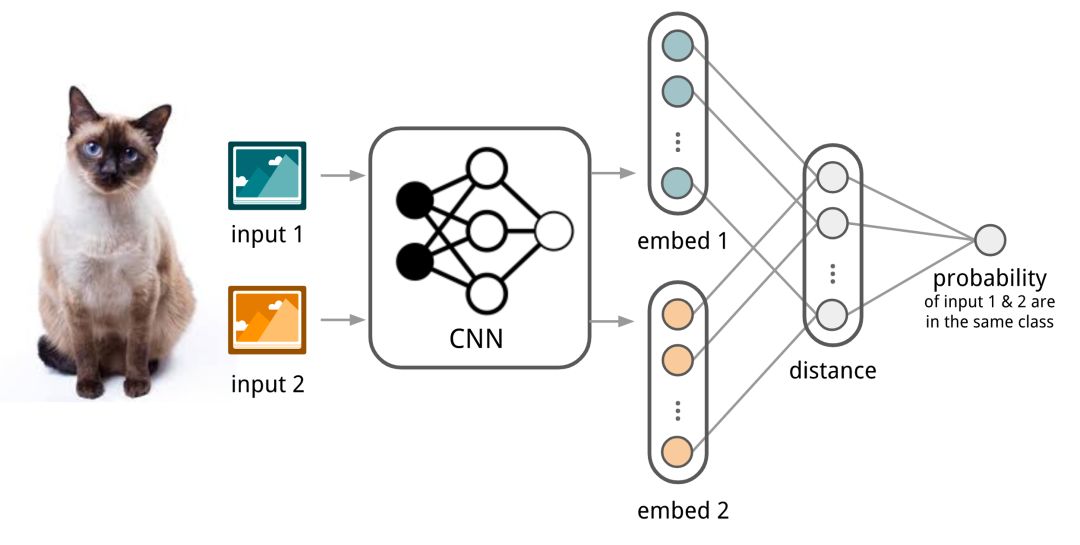
Siamese神经网络由两个网络组成,它们的输出在顶部联合训练,具有学习输入数据样本对之间关系的功能。两个网络是相同的,共享相同的权重和网络参数。换句话说,两者都指的是学习有效嵌入以揭示数据点对之间的关系的相同嵌入网络。
Koch,Zemel和Salakhutdinov(2015)提出了一种使用暹罗神经网络进行一次性图像分类的方法。首先,训练暹罗网络进行验证任务,以判断两个输入图像是否在同一类中。它输出属于同一类的两个图像的概率。然后,在测试时间期间,暹罗网络处理测试图像与支持集中的每个图像之间的所有图像对。最终预测是具有最高概率的支持图像的类。
首先,卷积Siamese网络学习通过包含一对卷积层的嵌入函数将两个图像编码成特征向量。
-
两个嵌入之间的L1距离是
。
-
通过线性前馈层和Sigmoid将距离转换为概率p.
它是从同一个类中抽取两个图像的概率。 直观地说,损失是交叉熵,因为标签是二元的。
-
当然,您可以将L1距离替换为其他距离度量,L2,余弦等。只需确保它们是差分,然后其他所有都相同。
给定支持集和测试图像,最终预测类是:
假设可以推广学习嵌入以用于测量未知类别的图像之间的距离。 通过采用预先训练的模型,这与迁移学习背后的假设相同; 例如,在使用ImageNet预训练的模型中学习的卷积特征有望帮助其他图像任务。 然而,当新任务偏离模型训练的原始任务时,预训练模型的益处减少。
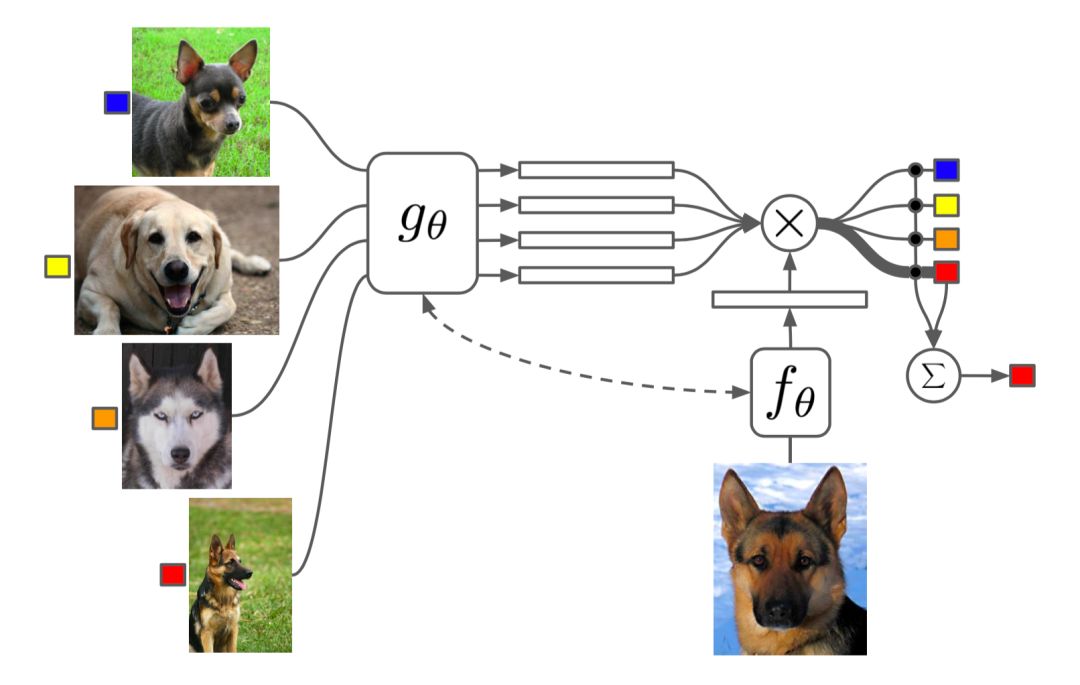
匹配网络
匹配网络的任务是为任何给定(小)支持集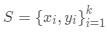
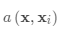
注意核依赖于两个嵌入函数f和g,分别用于编码测试样本和支持集样本。 两个数据点之间的注意力权重是它们的嵌入向量之间的余弦相似度,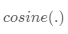
完整的上下文嵌入
嵌入向量是构建良好分类器的关键输入。 将单个数据点作为输入可能不足以有效地测量整个特征空间。 因此,匹配网络模型进一步提出通过将除了原始输入之外的整个支持集S作为输入来增强嵌入功能,使得可以基于与其他支持样本的关系来调整学习嵌入。
-
使用双向LSTM在整个支持集S的上下文中编码
-
将测试样本LSTM编码,并在支持集S上进行读取注意力。
-
首先,测试样本通过简单的神经网络(例如CNN)来提取基本特征
。
然后,作为隐藏状态的一部分,在支持集上使用读取注意向量训练LSTM:
该嵌入方法称为“全上下文嵌入(FCE)”。 有趣的是,它确实有助于提高硬任务的性能(在ImageNet上进行少量分类),但在简单任务上没有任何区别。
匹配网络中的训练过程旨在匹配测试时的推理。 值得一提的是,匹配网络论文改进了训练和测试条件应该匹配的想法。
关系网络
关系网络与Siamese网络类似,但有一些差异:该关系不是由特征空间中的简单L1距离获得,而是由CNN分类器测。 一对输入间的关系得分是其中连接。不是交叉熵,因为概念上关系网络更侧重于预测关系分数,更像是回归,而不是二元分类,
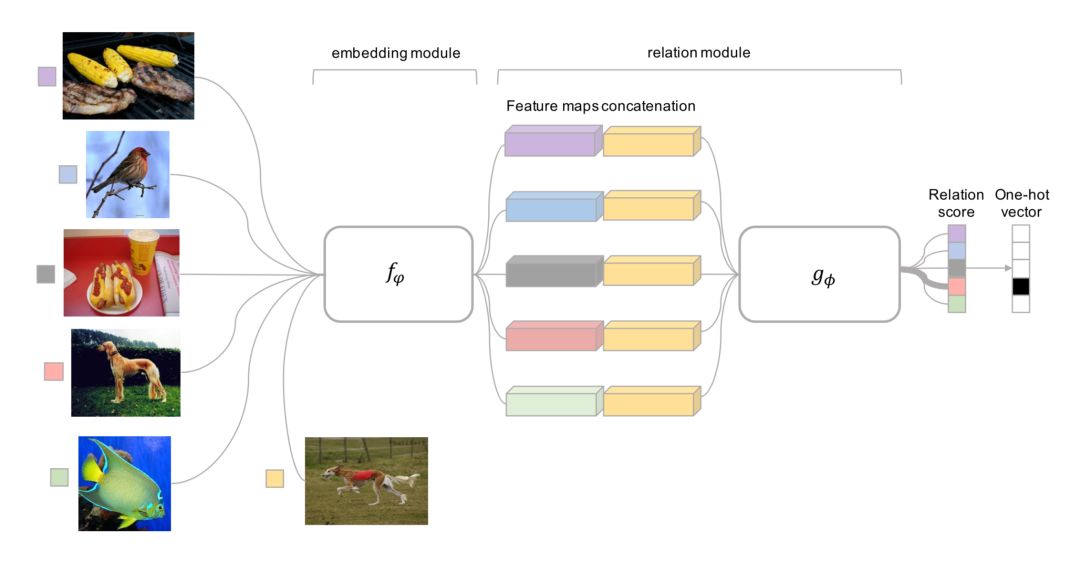
原型网络使用嵌入函数将每个输入编码为M维特征向量。 为每个类定义原型特征向量,作为该类中嵌入的支持数据样本的平均向量。
给定测试输入x的类上的分布是在测试数据嵌入和原型向量之间的距离的倒数上的softmax。
其中dφ可以是任何距离函数,只要φ是可微分的。 在论文中,他们使用了欧氏距离平方。
损失函数是负对数似然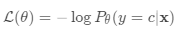
原文链接:
https://lilianweng.github.io/lil-log/2018/11/30/meta-learning.html
-END-
专 · 知
人工智能领域26个主题知识资料全集获取与加入专知人工智能服务群: 欢迎微信扫一扫加入专知人工智能知识星球群,获取专业知识教程视频资料和与专家交流咨询!
PC登录www.zhuanzhi.ai或者点击阅读原文,可以获取更多AI知识资料!
加入专知主题群(请备注主题类型:AI、NLP、CV、 KG等)可以其他同行一起交流~ 请加专知小助手微信(扫一扫如下二维码添加),
AI 项目技术 & 商务合作:bd@zhuanzhi.ai, 或扫描上面二维码联系!
请关注专知公众号,获取人工智能的专业知识!
点击“阅读原文”,使用专知