数学奥赛狂砍10题！Meta发布全新定理证明器：AI即将接管数学？

---

  新智元报道  

编辑：LRS

【新智元导读】人类主导的数学领域也要被AI攻克了？

张益唐教授最近发布的论文宣布攻克「郎道-西格尔零点猜想问题」，着实让数学之美火出了圈。

实际上每个定理的证明都需要天才般的灵感和不断尝试。论灵感一现，机器永远也比不上人类；但论刻苦能力，那AI模型可以甩人类十条街，给它资料它真学啊！

长期以来，科学界也一直将「AI能够自动进行定理证明」视为制造智能机器的关键一步。

要证明一个特定的猜想是真是假，需要用到符号推理，并在无数可能种可用方法中选择一条正常的方向。

最近Meta在NeurIPS 2022上发布了一个神经定理证明器（neural theorem prover），成功解决了10道国际数学奥林匹克（IMO）的问题，比之前最强的AI系统高5倍。该模型还在miniF2F数据集上比当前最先进的模型性能提高20%，在Metamath基准上提高10%

论文链接：https://arxiv.org/pdf/2205.11491.pdf

文中提出的全新搜索算法——超树证明搜索（HyperTree Proof Search， HTPS）灵感来自于AlphaZero

通过在线学习，HTPS在一个包含大量成功数学证明的数据集上学习搜索，使其能够泛化远离训练集的领域，即在新的且不同种类的问题仍然可用，最终HTPS能够对一个包含有限种情况的IMO问题推导出一个正确的证明。

实验结果表明，仅用HTPS算法就可以证明65.4%的Metamath定理，大大超过了之前GPT-f的56.5%的水平，对这些未被证明的定理进行的在线训练可以将准确率提高到82.6%

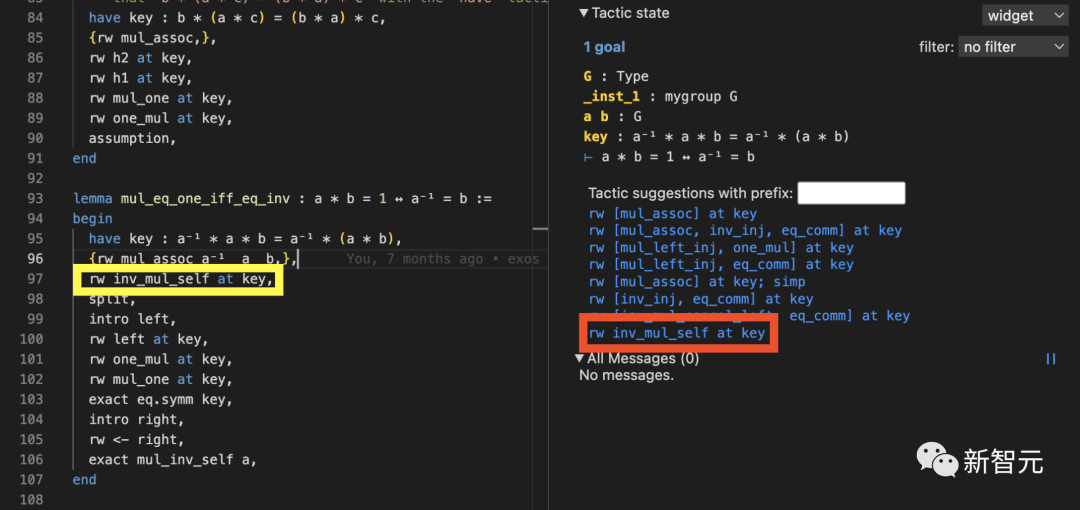
研究人员通过Lean Visual Studio Code插件提供了该模型，其他研究者可以在流行的Lean环境中继续探索该人工智能模型的功能。

数学题vs下围棋

国际数学奥林匹克IMO是世界首屈一指的高中数学竞赛。

自1959年以来，来自中学的学生们需要解决代数、组合数学、数论和几何中具有挑战性的问题，想要完成题目需要创造力和强大的推理技能，但有些问题太难了，以至于大多数学生都只能得零分。

专家们长期以来一直认为，想要建立一个可以在IMO中与人类抗衡的AI系统是一个巨大的挑战。

总体来说，定理证明比下围棋、国际象棋这样的棋盘游戏更具挑战性。

首先，当模型试图证明一个定理时，每一步可能的action空间不是很大，而是无穷大。

并且在国际象棋或围棋比赛中，即便某一步没有找到最优解，最终仍然有可能赢得对局；而对于定理证明来说，死胡同就是死胡同，一步做错，满盘皆输，之前的所有计算工作全是白费力气。

同时数学题中也可能存在特殊的解题方法，对于人类来说，可能属于最简单的一类问题，但从AI的角度来看，这种方法因为其特殊性，在标准训练数据中很少出现，所以AI很难学会。「暴力搜索」对这种无穷大的搜索空间来说也无能为力。

无论对人还是机器来说，想解决这类问题，必须依靠「创造性推理」方法。

之所以会出现这类问题，是因为之前的定理证明器过于依赖语言模型，虽然GPT-3等可以解决部分数学题，但它仍然探索不同方法的能力，这种技能对于解决需要「创造力」的数学问题来说至关重要。

接近人类的推理能力

数学推理的过程很难写，但更难量化。

目前相关研究方法主要集中在制造能够「立刻」解决问题的AI算法，即在一个step中生成一个完整的问题解决方案。

很明显，人肯定不是这么做数学题的，人类需要利用直觉，把一个复杂的问题分解成多个子问题，然后寻找增量式解决的方法。

为了模拟一种更「类人」的方法，需要神经定理证明程序将特定的「状态」与当前「对问题不完全的理解」联系起来。

研究人员采取的方法是利用强化学习与现有的证明辅助(如 Lean)结合搭建训练环境。

计算机证明辅助实现了一个逐步的推理机制，可以将(不完全)证明的「当前状态」解释为图中的一个节点，并将每个新步骤解释为一个边，这种方法已被证明是对围棋或国际象棋等双人游戏非常有效的技术。

最后，还需要一种方法来评估证明状态的质量，类似于下棋的人工智能需要评估游戏中的每个位置对于局势的影响。

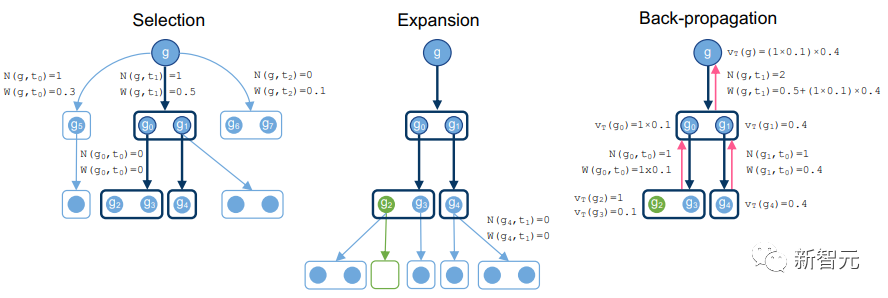
研究人员使用了蒙特卡罗树搜索(MCTS)启发的方法，其中模型在两个任务之间循环：1）在给定的证明状态下使用的合理参数的先验估计；2）给定一定数量的参数后的证明结果。

HTPS 是标准 MCTS 方法的一个变体。在这种方法中，为了探索一个图，人们利用关于图的先验知识来选择一组叶子来展开，然后通过备份校正来精炼初始知识。图是逐步探索的，关于图结构的知识通过迭代得到细化。

这样就可以使用在线训练程序，从而大大提高最初预训练的模型在某一类问题上的表现，即可以解决类似于IMO竞赛中的问题。

最后的实验结果显示，该方法能够解决10个未见过的IMO问题，并且在Minif2f验证集准确性方面达到67% 的准确性ーー比目前公布的最新技术水平高出整整20% 。

从软件验证到航空航天

制造出能够解决高等数学问题的AI模型将对现实世界产生影响，尤其是在软体验证领域。

许多公司(包括 Meta)都在使用形式证明来验证软件。事实上，用于验证软件和证明定理的工具和形式系统是相同的，主要区别在于模型所依据的数据类型: 函数数据集或数学定理。

除了软体验证，还有许多工业应用，尤其是在复杂性不断增加、自动化渗透到关键任务中的情况下，包括密码学和航空航天，其中操作条件可以变化，测试和模拟是至关重要的。

参考资料：

https://ai.facebook.com/blog/ai-math-theorem-proving/