世界本来已经很卷,有了 AI 加入之后,卷上加卷……
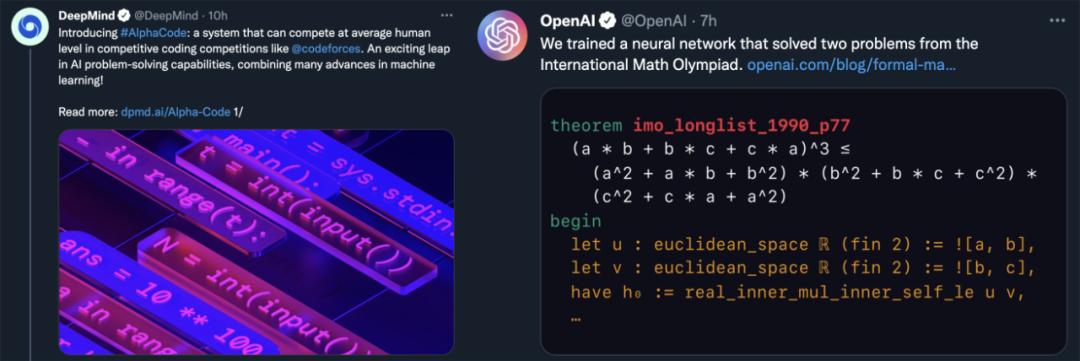
在国内欢度春节之时,DeepMind 与 OpenAI 两个知名 AI 研究机构分别发布重要研究成果:DeepMind 发布了基于 Transformer 模型的 AlphaCode,可以编写与人类相媲美的计算机程序;同时,OpenAI 开发的神经定理证明器成功解出了两道国际奥数题。
![]()
虽然两家研究机构的新成果为 AI 解决老问题提供了新思路,但也不得不让网友感叹,AI 领域太卷了!
![]()
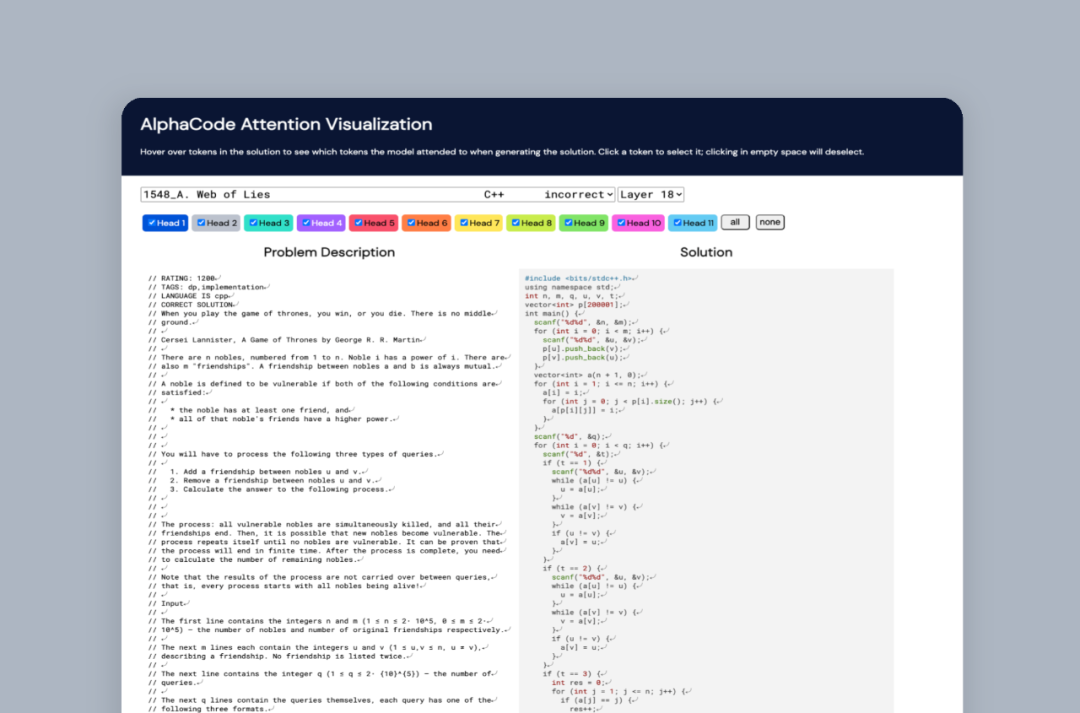
在最近的一篇论文中,DeepMind 的研究者介绍了 AlphaCode。AlphaCode 使用基于 Transformer 的语言模型实现大规模的代码生成,并且将其编写为程序。
![]()
论文连接:https://storage.googleapis.com/deepmind-media/AlphaCode/competition_level_code_generation_with_alphacode.pdf
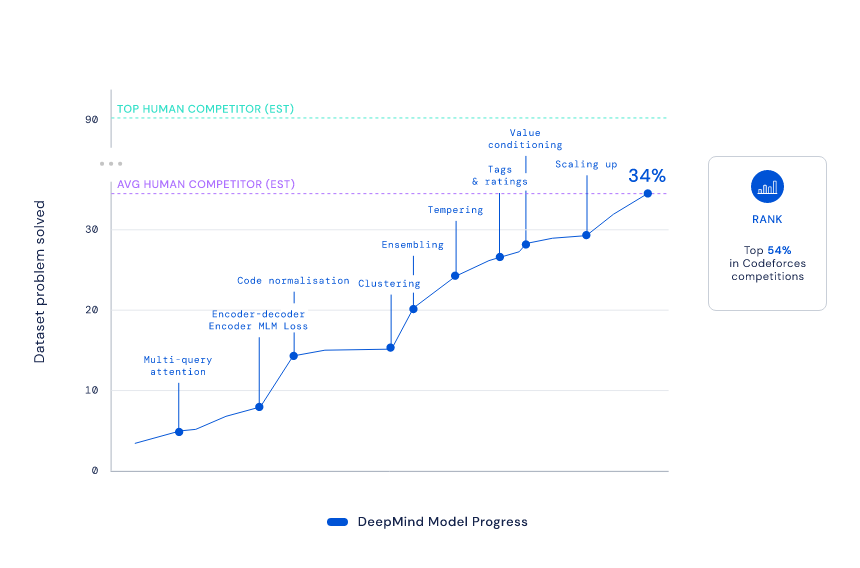
研究者将 AlphaCode 放在 Codeforces 挑战中进行了测试,Codeforces 是一个具有竞争力的编程平台,它类似于国际象棋中使用的 Elo 评级系统,每周分享编程挑战和问题排名。不同于编程人员在打造商业应用程序时可能面临的任务,Codeforces 的挑战更加独立,需要对计算机科学中的算法和理论概念有更广泛的了解,一般是结合逻辑、数学和编码专业知识的非常专业的难题。
AlphaCode 针对 Codeforces 网站上 5000 名用户解决的 10 项挑战进行了测试,总体排名位于前 54.3%,也就是说它击败了 46% 的参赛者 。DeepMind 估计,AlphaCode 系统的 Codeforces Elo 为 1238,使其过去六个月内在该网站上竞争的用户中排名前 28%。
![]()
举个例子,在测试 AlphaCode 的一项挑战中,试题要求参赛者找到一种方法,使用一组有限的输入将一个随机、重复的 s 和 t 字母字符串转换为另一个相同字母的字符串。例如,竞争对手不能只输入新字母,而必须使用「backspace」命令删除原始字符串中的几个字母。对于 AlphaCode 来说,这只是中等难度的挑战:
![]()
其中十个挑战以与人类完全相同的格式输入 AlphaCode。然后,AlphaCode 生成大量可能的答案,并通过运行代码和检查输出来筛选这些答案,就像人类竞争对手一样。AlphaCode 论文的联合负责人 Yujia Li 和 David Choi 表示:「整个过程是自动的,无需人工选择最佳样本。」
要想在 Codeforces 的挑战中脱颖而出,原本不是一件容易的事。AlphaCode 项目开展于两年多前,随着大规模 Transformer 模型的进步与大规模采样、滤波技术的结合,DeepMind 的研究者已经在 AI 能够解决的问题数量上取得了重大进展。
![]()
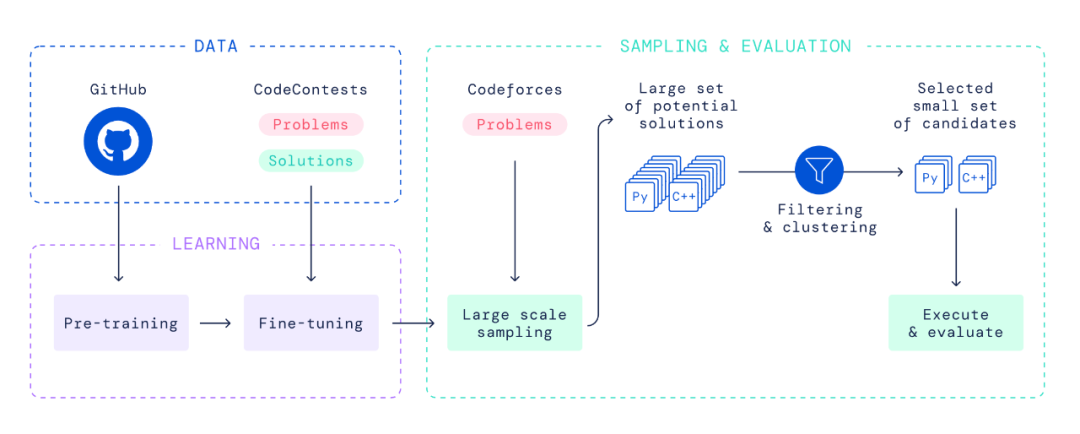
研究者在选定的公共 GitHub 代码上预训练该模型,并在相对较小的竞赛编程数据集上对其进行微调。在评估期间,研究者为每个问题创建了大量的 C++ 和 Python 程序,且数量级比以前的工作要大。然后对这些解决方案进行筛选、聚类和重新排序,将这些解决方案分配到一个由 10 个候选程序组成的小集合中,并提交给外部评估。这个自动化系统取代了竞争对手的调试、编译、通过测试和最终提交的反复试验过程。
![]()
总体来说,AlphaCode 的排名在竞争对手中大致相当于中位数。虽然远远没能赢得比赛,但这个结果代表了人工智能解决问题能力的实质性飞跃。这一进步证明了深度学习模型在需要批判性思维的任务中的潜力。DeepMind 指出,AlphaCode 目前的技能组合目前仅适用于竞赛性质的编程领域,但它的能力为创建未来工具打开了新的大门,这些工具使编程变得更加容易,并且有朝一日完全自动化。
许多其他公司正在开发类似的应用程序。对于终端的用户来说,这些系统就像 Gmail 的 Smart Compose 功能一样工作,提供一些关于你正在编写的任何内容的建议。
近年来,AI 编程系统的开发取得了很大进展,但这些系统还远未准备好接管人类程序员的工作。他们生成的代码通常有问题,而且由于系统通常是在公共代码库上进行训练的,所以有时会复制受版权保护的材料。
在一项关于 GitHub Copilot AI 编程工具的研究中,研究人员发现其输出的代码约有 40% 包含安全漏洞。安全分析师甚至建议,不良行为者可以故意编写代码并与隐藏的后门(backdoor)在线共享代码,然后这些代码可能被用来训练 AI 程序,将这些错误插入到未来的程序中。
像这样的挑战意味着 AI 编程系统可能会慢慢融入程序员的工作中——换句话说,他们要进行学徒训练,从助理开始做起,在被信任能够自主执行工作之前,AI 给出的建议都要受到怀疑。
![]()
目前,DeepMind 已在 GitHub 上发布了竞赛级编程问题和解决方案的数据集,其中也包括广泛的测试的数据,以确保通过这些测试的程序是正确的,这是目前数据集所缺乏的一个关键特性。DeepMind 希望这个基准能够推动在解决问题和代码生成方面的进一步创新。
GitHub 项目地址:https://github.com/deepmind/code_contests
在学科竞赛领域,国际数学奥林匹克竞赛(IMO)是非常有名的一个,我们熟悉的很多数学大神(如韦东奕)都在这一竞赛中取得了骄人的成绩。
2021 年,这项比赛迎来了一个微小的变化:微软研发多年的数学 AI——Lean 也加入了竞争,和人类选手一决高下。据悉,Lean 是微软研究院在 2013 年推出的计算机定理证明器:数学家可以把数学公式转换成代码,再输入到 Lean 中,让程序来验证定理是否正确。
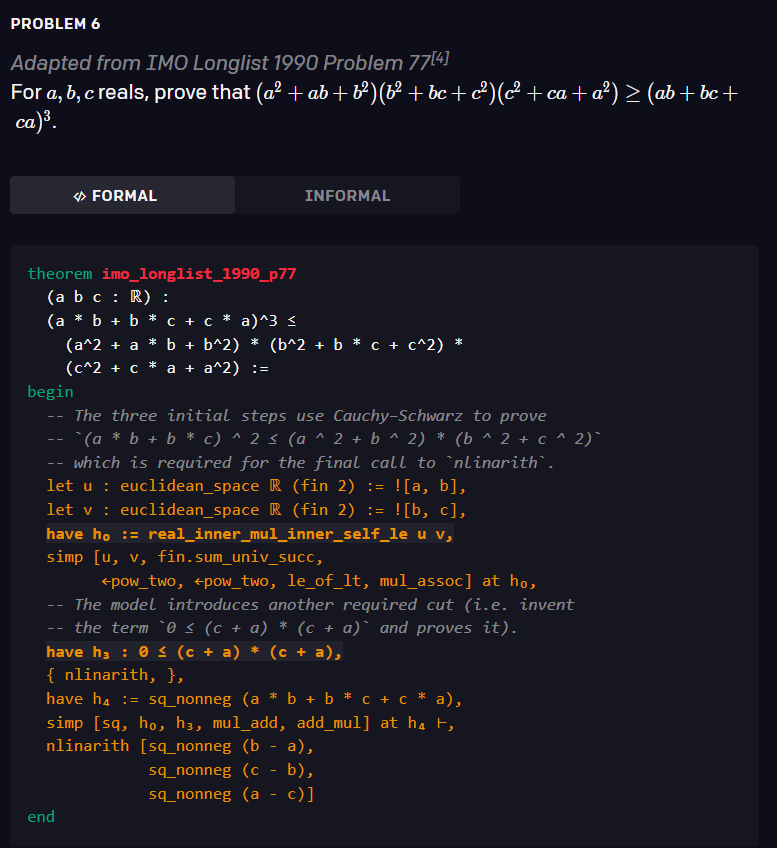
由于 Lean 剑指金牌,研究人员一直在对其进行不停的打磨,其中也包括被微软收购了的 OpenAI。刚刚,OpenAI 发文表示,他们已经为 Lean 创建了一个神经定理证明器,用于解决各种具有挑战性的高中奥林匹克问题,包括两个改编自 IMO 的问题和来自 AMC12、AIME 竞赛的若干问题。
该证明器使用一个语言模型来寻找形式化命题(formal statement)的证明。每次发现一个新的证明,研究者就把它作为新的训练数据,这改善了神经网络,使它能够在迭代中找到越来越难的命题的解决方案。
该证明器在 miniF2F 基准测试中实现了 SOTA(41.2% vs 29.3%)水平,miniF2F 包含一组具有挑战性的高中奥林匹克问题。
研究者将他们的方法称为 statement curriculum learning,该方法包括手动收集的一组不同难度级别的命题(无需证明),其中最难的命题类似于目标基准。最初,他们的神经证明器很弱,只能证明其中的几个。因此,他们迭代地搜索新的证明,并在新发现的证明上重新训练他们的神经网络。经过 8 次迭代,他们的证明器在 miniF2F 上取得了出色的成绩。
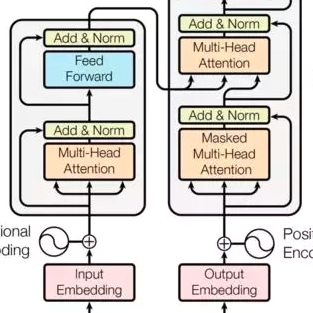
形式化数学(formal mathematics)是一个令人兴奋的研究领域,因为:1)它很丰富,可以让你证明需要推理、创造力和洞察力的任意定理;2)它与游戏相似,也有一种自动化的方法来确定一个证明是否成立(即由形式系统验证)。如下图中的例子所示,证明一个形式化的命题需要生成一系列的证明步骤,每个证明步骤都包含对策略( tactic)的调用。
形式化系统接受的 artifact 是低级的(就像汇编代码),人类很难产生。策略是从更高层次的指令生成这种 artifact 的搜索过程,以辅助形式化。
这些策略以数学术语作为参数,每次策略调用都会将当前要证明的命题转换为更容易证明的命题,直到没有任何东西需要证明。
![]()
研究者观察到,生成策略参数所需的原始数学术语的能力出现在了他们的训练过程中,这是离开神经语言模型所无法完成的。下面的证明就是它的一个例子:证明步骤「use n + 1」(完全由模型生成)提出使用「n + 1」作为解决方案,剩下的形式证明依赖于「ring _ exp」策略来验证它确实有效。
![]()
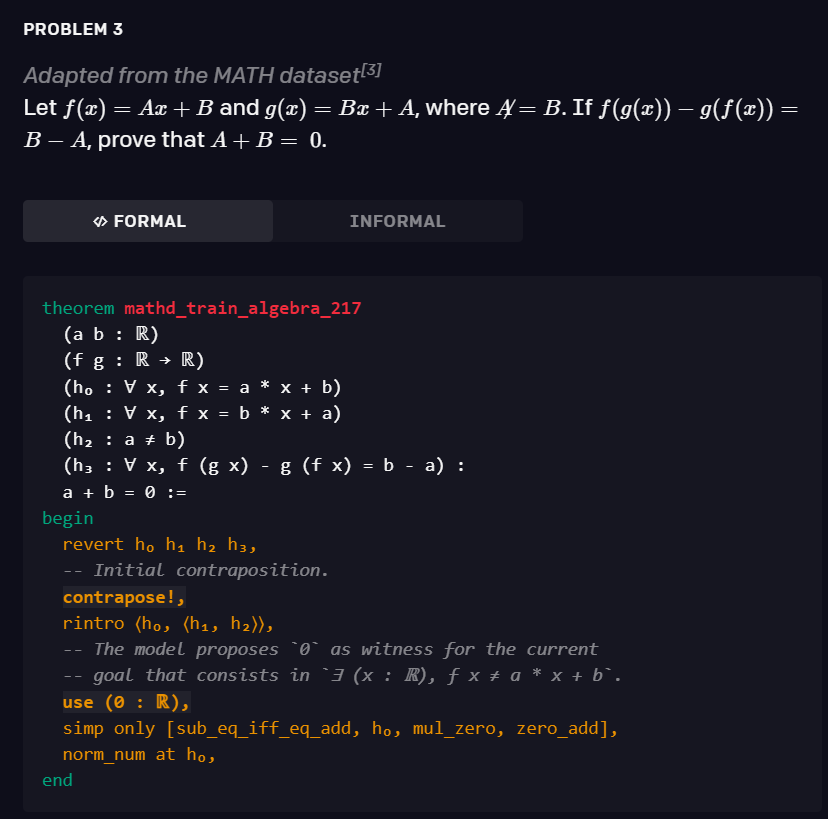
研究者还观察到,他们的模型和搜索过程能够产生链接多个重要推理步骤的证明。在下面的证明中,模型首先使用了引出存在性命题(existential statement) (∃ (x : ℝ), f x ≠ a * x + b) 的换质换位律(contraposition)。然后,它使用 use (0 : ℝ) 为它生成一个 witness,并通过利用 norm _ num 策略来完成证明。
![]()
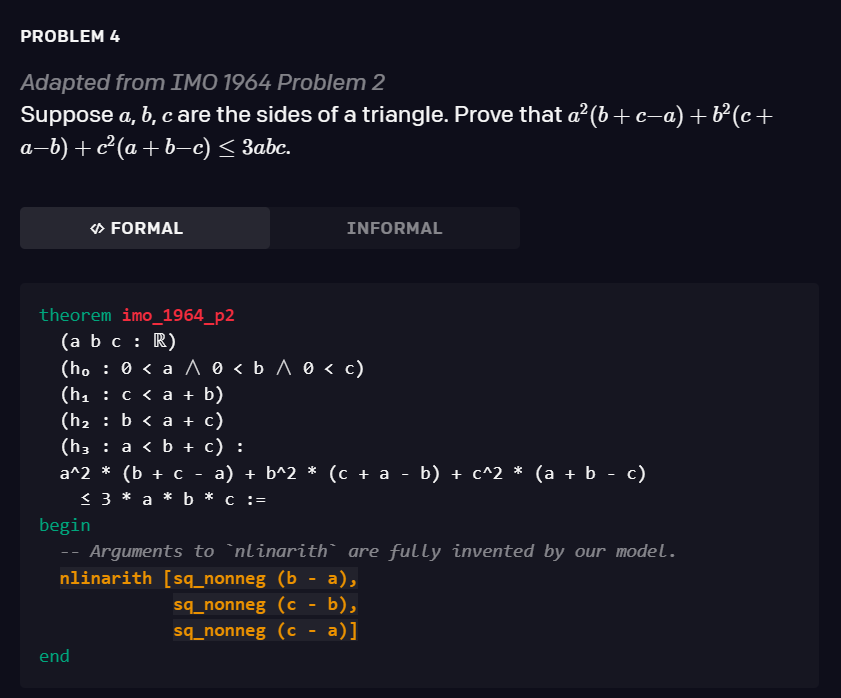
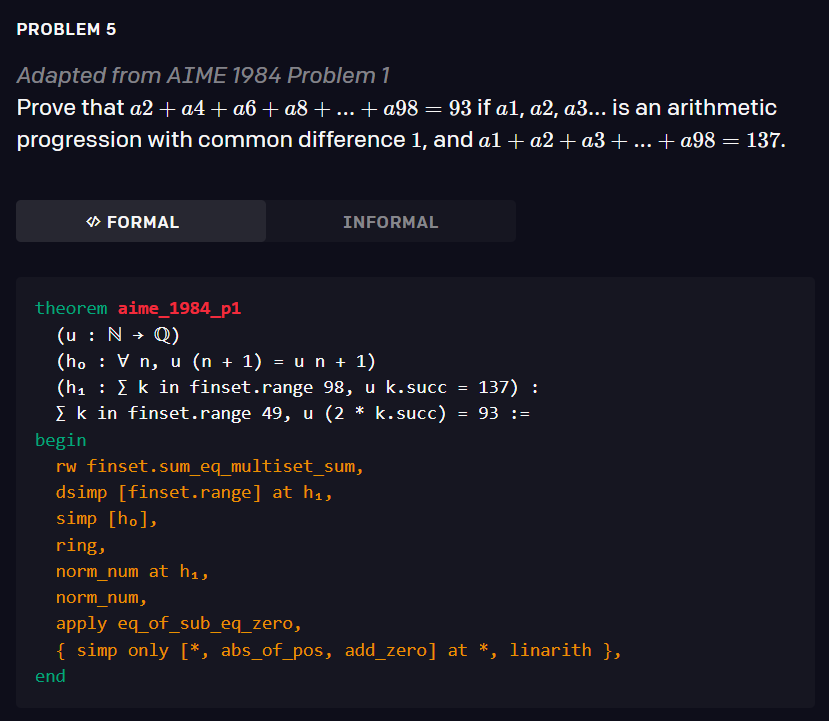
该模型经过 statement curriculum learning 的训练,能够解决培训教材以及 AMC12 和 AIME 中的各种问题,以及改编自 IMO 的两个问题。下面是三个有关的例子。
![]()
![]()
![]()
形式数学涉及两个主要的挑战,使得单纯的强化学习应用不太可能成功:
1. 无限的动作空间:形式数学不仅有超大的搜索空间(比如像围棋),还有无限的动作空间。在搜索证明的每个步骤,模型的选择范围不是一组行为良好的有限动作,而是一组复杂且无限的策略,涉及必须生成的外生数学术语(例如,生成用作 witness 的数学命题)。
2. 缺乏自博弈(self-play):与两人游戏相反,证明器不是与对手对抗,而是与一系列需要证明的命题对抗。当面对一个过于困难的命题时,没有明显的重构可以让证明器首先生成更容易处理的中间语句。这种不对称性阻止了在双人游戏中获得成功的自博弈算法的简单应用。
在这项工作中,研究者通过从一个语言模型中采样动作来解决无限动作空间问题。语言模型能够生成策略调用以及通常需要作为参数的原始数学术语。对于自博弈的缺乏,他们观察到,自博弈在两人游戏中的关键作用是提供一个无监督的课程(curriculum)。因此,他们建议用一套不同难度的辅助问题命题(不需要证明)来代替这种无监督的课程。他们的实验结果表明,当这些辅助问题的难度变化足够大时,他们的训练程序就能够解决一系列越来越难的问题,最终推广到他们所关心的问题集。
虽然这些结果非常令人兴奋,因为它们证明了深度学习模型在与形式系统交互时能够进行重要的数学推理,但在竞赛中,该证明器离最佳学生表现还差得很远。研究者表示,他们希望自己的工作将推动这一领域的研究,特别是针对 IMO 的研究,并希望他们提出的 statement curriculum learning 方法能够加快自动推理的研究进展。
两家机构最新的研究成果已经介绍完毕,网上已经零零散散地出现了关于效果的评价:
![]()
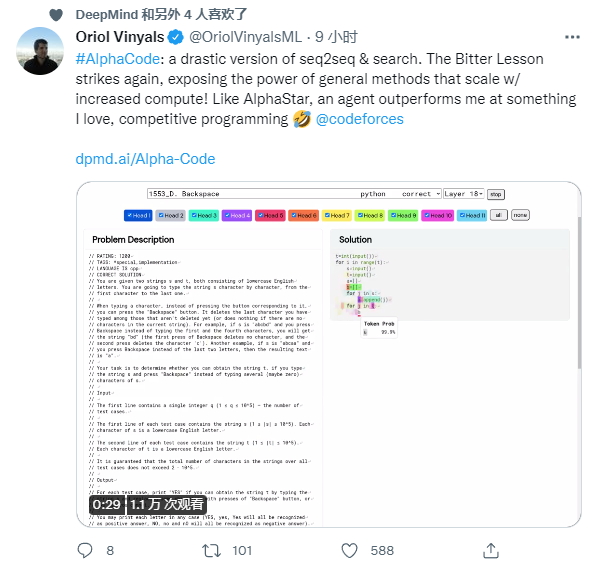
如有 AI 研究科学家发系列长推表示,AlphaCode 达到人类水平还需要几年时间,它在 codeforce 上的排名是有限制的,如许多参与者是高中生或大学生;还有就是 AlphaCode 生成的绝大多数程序都是错误的,正是使用示例测试进行过滤才使得 AlphaCode 实际解决了某些问题。
也有研究人员表示,这像是 AlphaStar 大力出奇迹的结果。
![]()
国内的 AI 从业者们可以趁假期研究下这两项研究,发表自己的看法。
参考链接:https://openai.com/blog/formal-math/?continueFlag=6cc759bbfb87d518f6d6948bcf276707
https://deepmind.com/blog/article/Competitive-programming-with-AlphaCode?continueFlag=b34ed7683541bab09a68d7ab1d608057
![]()
© THE END
转载请联系本公众号获得授权
投稿或寻求报道:content@jiqizhixin.com