DeepMind提出通用神经算法学习器,排序、搜索、动态规划全部解决

©作者 | 机器之心编辑部
来源 | 机器之心
来自 DeepMind 等机构的研究者提出了一个通用神经算法学习器,其能够学习解决包括排序、搜索、贪心算法、动态规划、图形算法等经典算法任务,达到专家模型平均水平。
然而,多数神经网络在 OOD 方面表现不佳。事实上,可以进行神经推理的架构需要算法对齐、自监督学习等其他算法的辅助。更进一步讲,这些模型需要在基于观察的基础上,对生成的新知识有一定的稳健性,特别是当这些知识脱离训练数据域时。
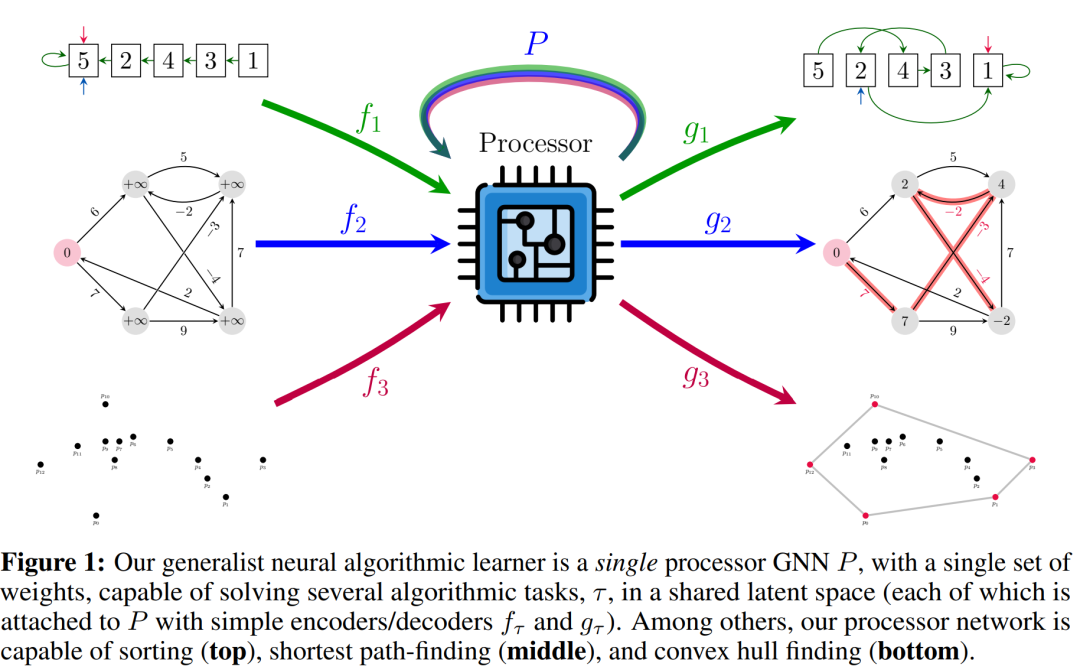
本文中, 来自 DeepMind 等机构的研究者提出一个通用神经算法学习器:具有单一参数集的 GNN,其能够同时学习解决经典算法任务,包括排序、搜索、贪心算法、动态规划、图形算法、字符串算法和几何算法,达到专家模型平均水平。
具体地,该研究利用 CLRS 基准从实证上表明,就像在感知领域取得的成功一样,通用算法学习器可以通过整合知识来构建。也就是说,只要我们能学会在单任务模式下很好地执行算法,就有可能在多任务模式下有效地学习算法。
受此启发,该研究对 CLRS 的输入表示、训练机制和处理器架构进行一系列改进,与现有技术相比,改进后的平均单任务性能提高了 20% 多。然后,本文利用这些改进对多任务学习器进行消融实验。结果表明,通用学习器能够有效地整合由专家模型捕获的知识。
论文链接:
可以说这项研究是一个重要的里程碑,表明即使在具有完全不同的控制流任务中,该研究也可以有意义地整合推理能力,并在多个任务中超过相应的单任务专家的 OOD 性能。
正如佐治亚理工学院机器学习博士生 Aran Komatsuzaki 所总结的:「本文构建了一个通用神经算法学习器,能够学习执行各种算法的单个 GNN 处理器,例如排序、搜索、动态规划、路径查找和几何。」
研究介绍
研究者提出的通用神经算法学习器如下图 1 所示。
论文第 3 章是主旨部分,主要介绍了表示、训练机制和架构的改进,使得单个模型的性能明显优于之前在 CLRS-30 上发布的 SOTA 技术。
CLRS 基准定义了五种类型的特性:标量(scalar)、分类、掩码、mask_one 和指针,它们都有自己的编码和解码策略以及损失函数。
本文中具体的改进包括但不仅限于:
数据集和训练:移除 teacher forcing。在评估时,模型无法访问数据集中的 hint,只能依靠已有的 hint 进行预测。在先前的模型中,训练期间提供了概率为 0.5 的 ground-truth hint,在没有 teacher forcing 的情况下,当存在 scalar hints 时,损失倾向于沿轨迹无界增长,从而破坏了训练的稳定性。
这项工作整合了几个重要的稳定变化,足以完全消除 teacher forcing 带来的影响,使训练与评估保持一致。由于 teacher forcing 的存在,排序算法和 Kruskal 算法的性能显著下降。在移除了 teacher forcing 之后,本文还对训练数据进行了扩充,以防止模型过拟合。
Soft hint 传播。本文将 softmax 用于分类,mask_one 、指针类型、logistic sigmoid 用于掩码类型。如果没有这些 soft hints,排序算法的性能会下降(类似于有 teacher forcing 的情况)。
利用编码器初始化和梯度裁剪提高训练稳定性。该研究使用 Xavier 进行初始化,从而有效地减少了输入维度仅为 scalar hint 的初始权重。此外,该研究还对编码器、解码器、网络处理器进行了改进。
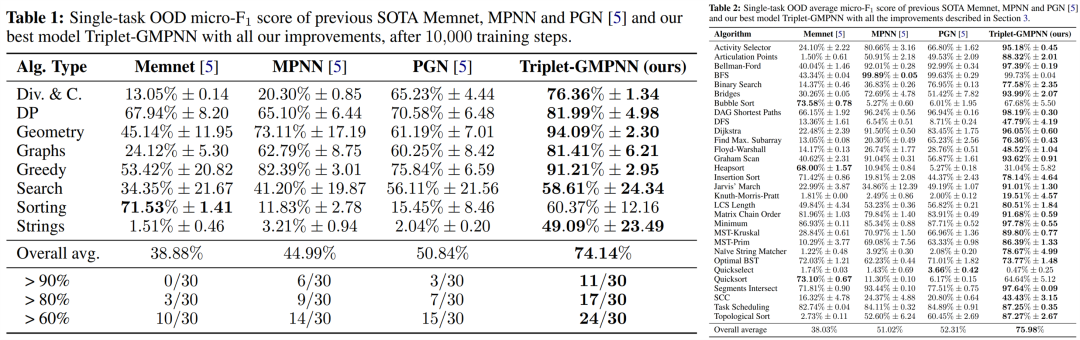
对模型改进之后得到一组超参数模型,经过训练,该模型在 CLRS-30 上达到了 SOTA 性能。下表 1 和表 2 显示了包括 Memnet、MPNN、PGN 等模型在内的 micro-F_1 得分。
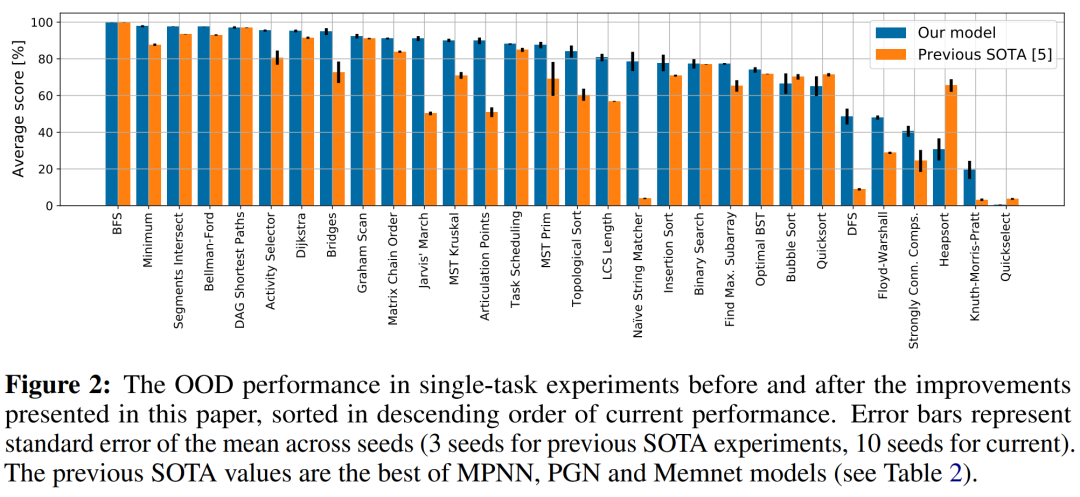
下图 2 显示了改进模型与 SOTA 模型之间的比较。本文的模型比次优模型(见表 1)平均性能提高了 20% 以上,并且除了一个算法系列之外,所有算法的性能都比其他模型有了显著提高。
从实验可以看出,有两个算法系列具有显著的 OOD 性能改进:第一个是几何算法,现在求解接准确率约 94% OOD ,而之前的最佳结果约为 73%;第二个是字符串算法,模型现在求解准确率超过 49%,而之前的最佳值约为 3%。与之前的 SOTA 相比,本文在 24 种算法中准确率超过 60%,17 种算法的准确率超过 80%,11 种算法的准确率超过 90%。
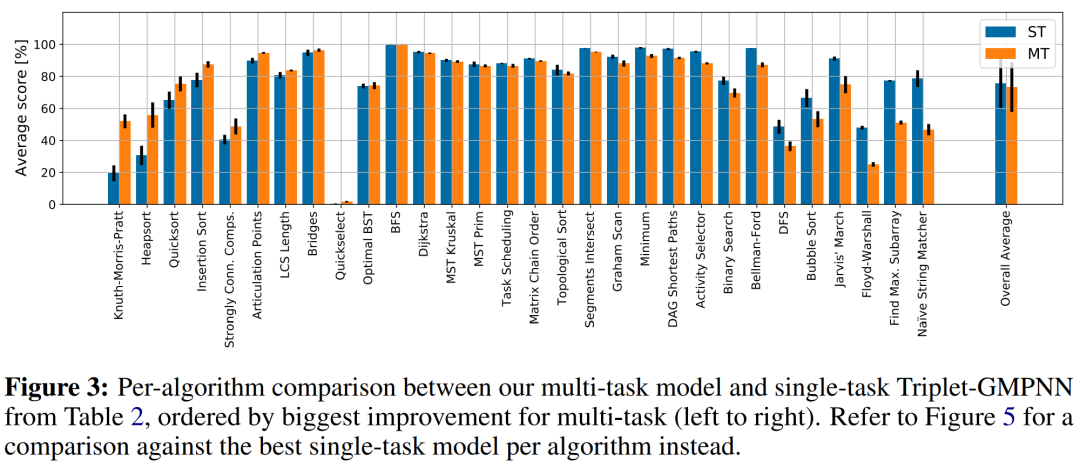
下图 3 比较了单任务 Triplet-GMPNN 与多任务模型的性能。
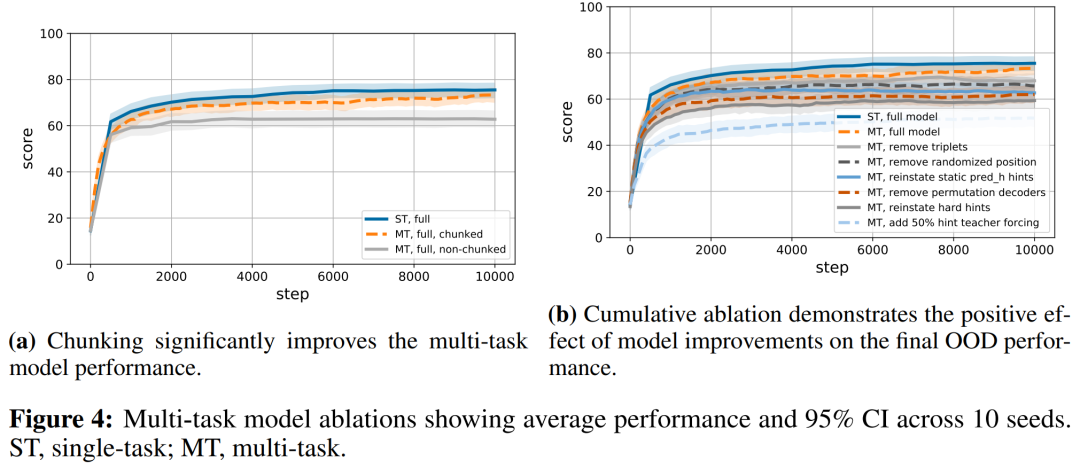
为了独立评估模型改进的效果,该研究还进行了消融实验。下图 4a 显示了 vanilla 训练和分块训练在性能上的显著差异;图 4b 显示了累积消融的结果:逐渐删除单个改进部分的结果。
更多阅读


#投 稿 通 道#
让你的文字被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个,让知识真正流动起来。
📝 稿件基本要求:
• 文章确系个人原创作品,未曾在公开渠道发表,如为其他平台已发表或待发表的文章,请明确标注
• 稿件建议以 markdown 格式撰写,文中配图以附件形式发送,要求图片清晰,无版权问题
• PaperWeekly 尊重原作者署名权,并将为每篇被采纳的原创首发稿件,提供业内具有竞争力稿酬,具体依据文章阅读量和文章质量阶梯制结算
📬 投稿通道:
• 投稿邮箱:hr@paperweekly.site
• 来稿请备注即时联系方式(微信),以便我们在稿件选用的第一时间联系作者
• 您也可以直接添加小编微信(pwbot02)快速投稿,备注:姓名-投稿
△长按添加PaperWeekly小编
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧