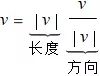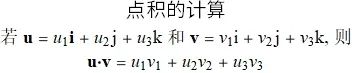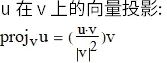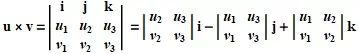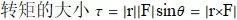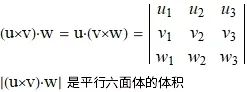修订版【笛卡尔坐标/点积/叉积】图解高等数学-下 03

10 空间中的向量和运动

当一个物体在空间中运动时, 其坐标方程 x=f(t), y=g(t), z=h(t) 提供了物体运动和路径的方程, 坐标为时间的函数. 如果采用向量记号, 可以把这些方程缩写为一个方程作为关于时间的向量函数的物体位置.

10.1 空间中的笛卡尔(直角)坐标和向量

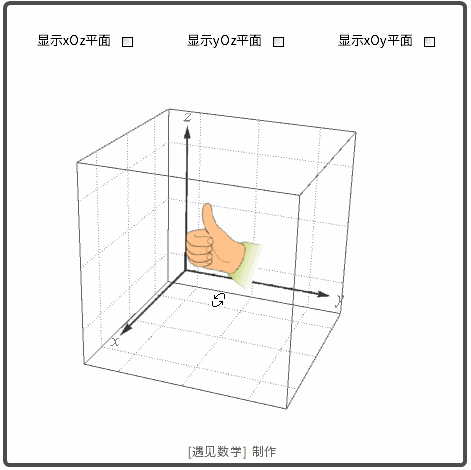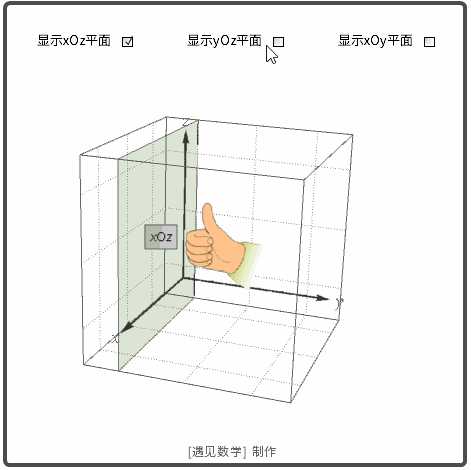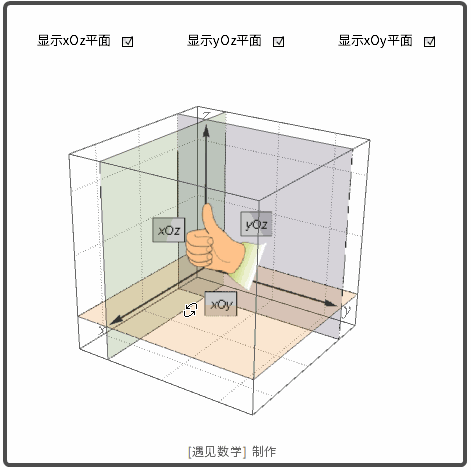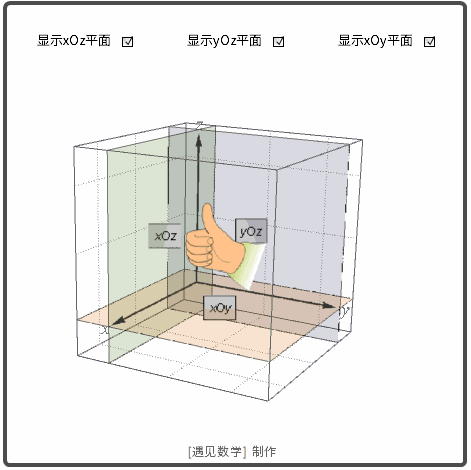
为给空间的点定位, 需要由三条相互垂直的轴. 如下图所示轴组成右手坐标系

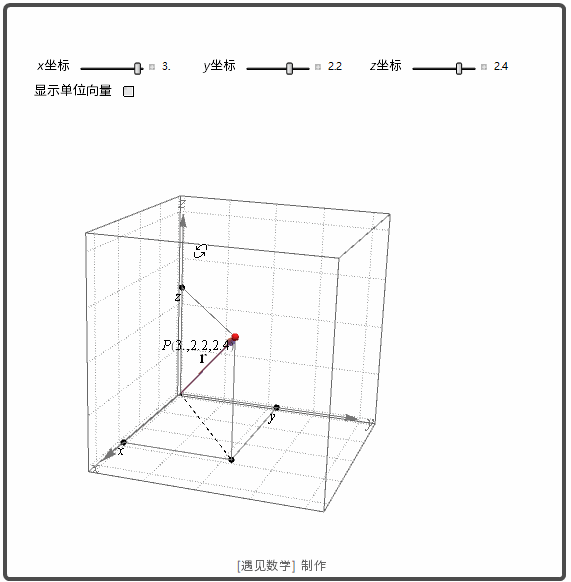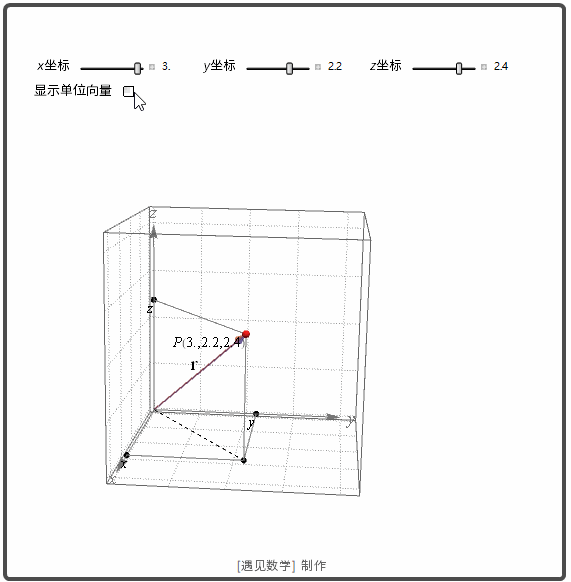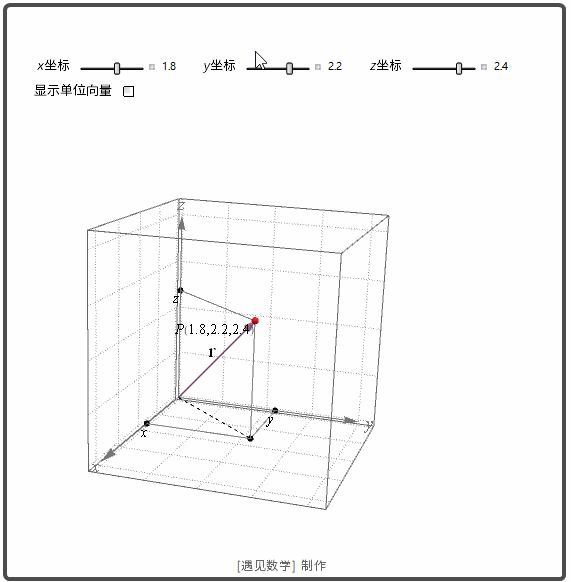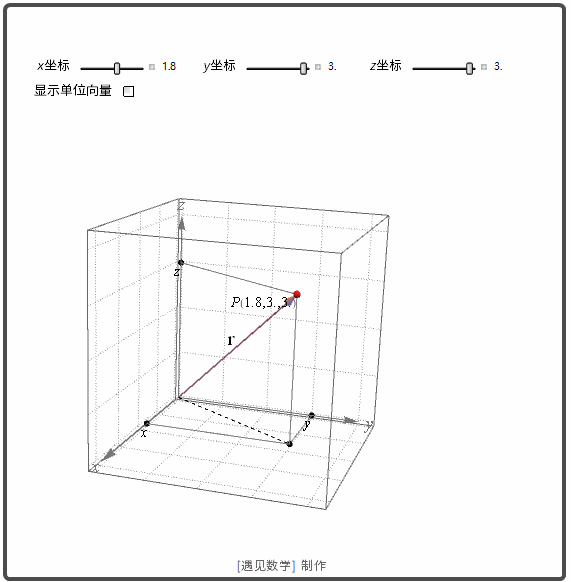
空间的点 P 的笛卡尔坐标 (x,y,z) 可用其位置向量表示. 如下图所示. 笛卡尔坐标也是直角坐标, 因为定义这种坐标的轴以直角相交.

空间中的向量

长度和方向与平面的情形一样, 若 v !=0 是空间中的非零向量, 则 v/|v| 是一个在 v 方向的单位向量. v 可以表示成它的长度和方向的乘积.

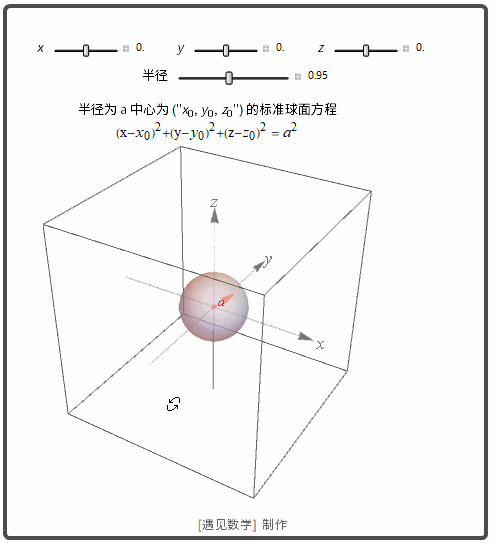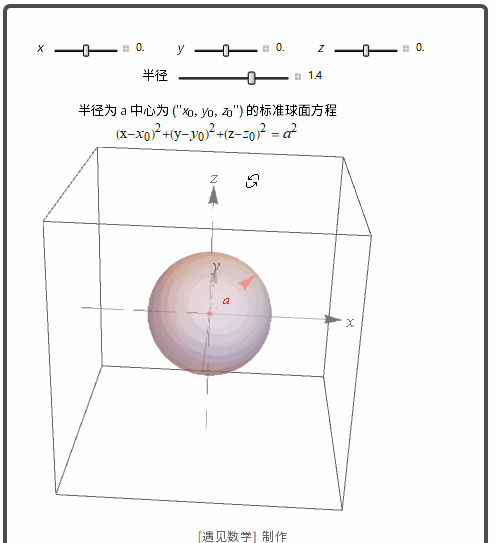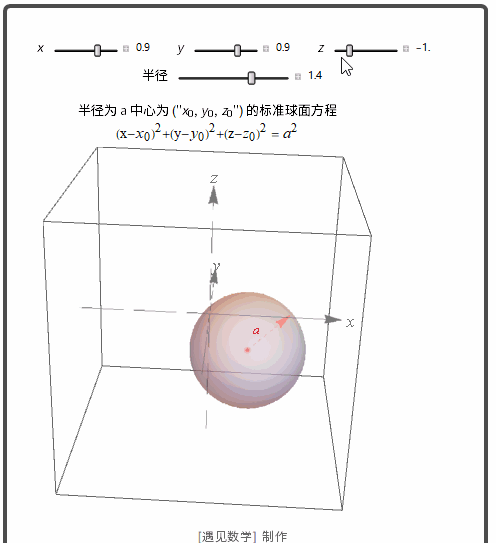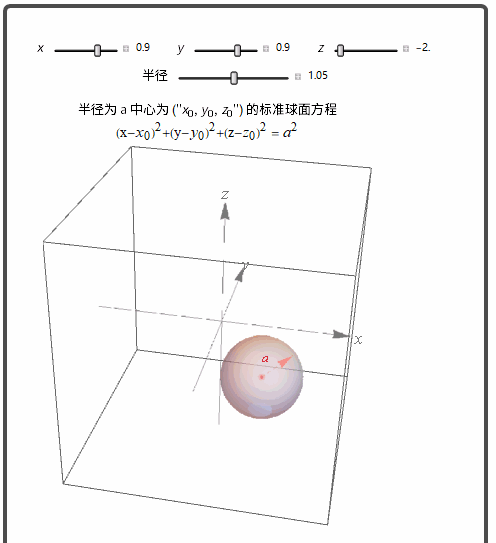
距离和空间中的球

半径为 a 中心为 (x0,y0,z0) 的标准球面方程:

---

10.2 点积和叉积

将之前研究的点积定义推广到空间. 然后对空间中的向量引入一个新的积, 称为叉积. 

点积

空间中两个向量的点积(或内积, 数量积)以对平面向量同样的方式定义. 当把两个非零向量 u 和 v 的起点放在一起, 就形成一个大小 0<=θ<=π 的角.

垂直(正交)向量和投影

跟平面向量的情形一样, 两个非零向量 u 和 v 是垂直或正交的, 当且仅当 u·v=0 .

如果 u 表示一个力, 那么 ${\text{proj}}_{v}u$ 表示在方向 v 的有效力.

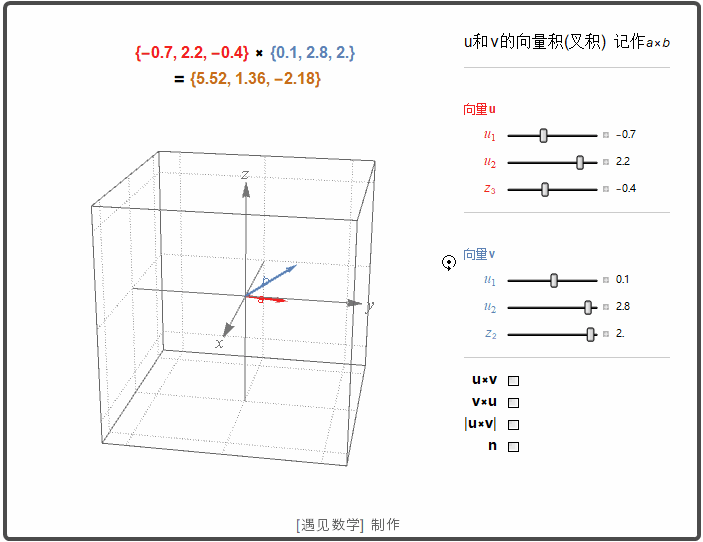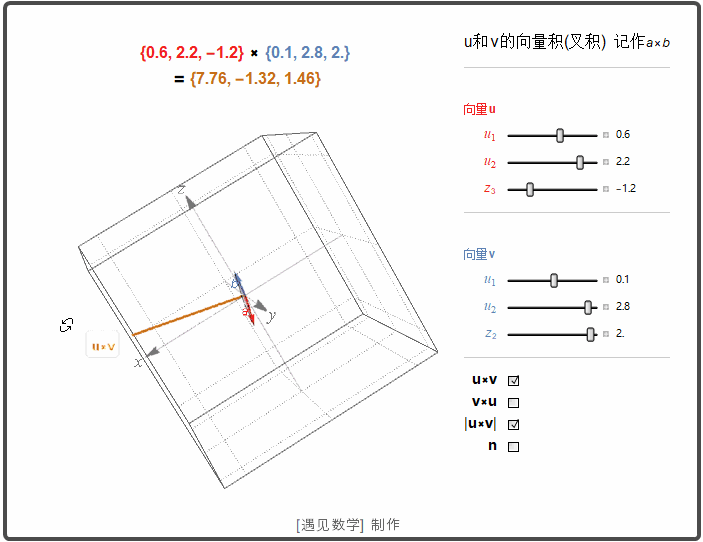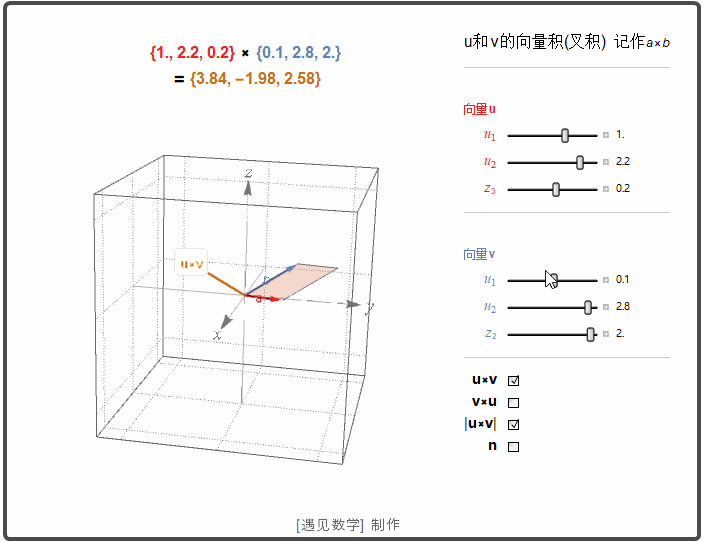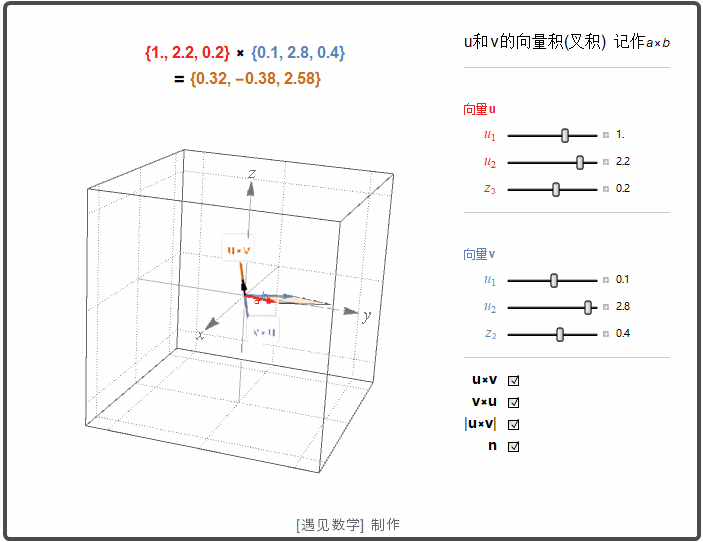
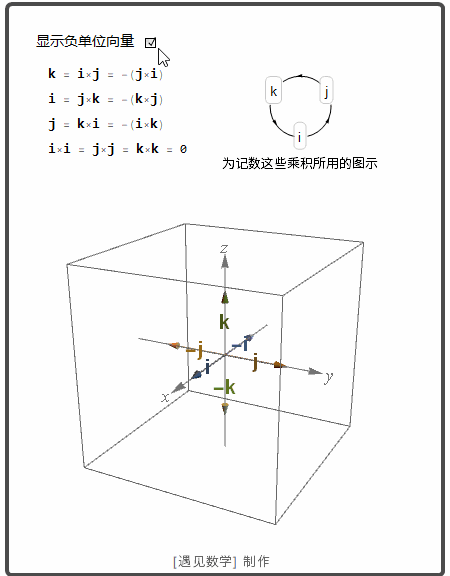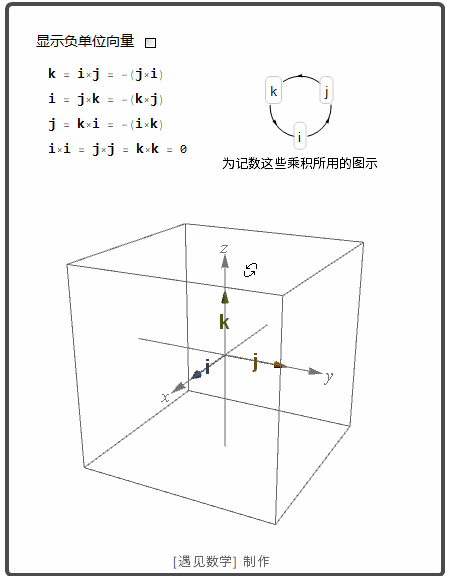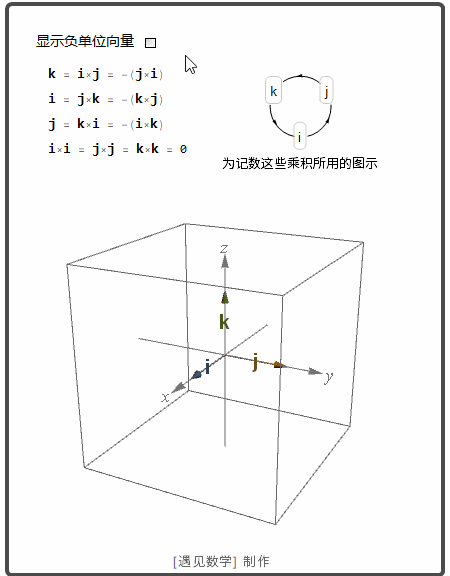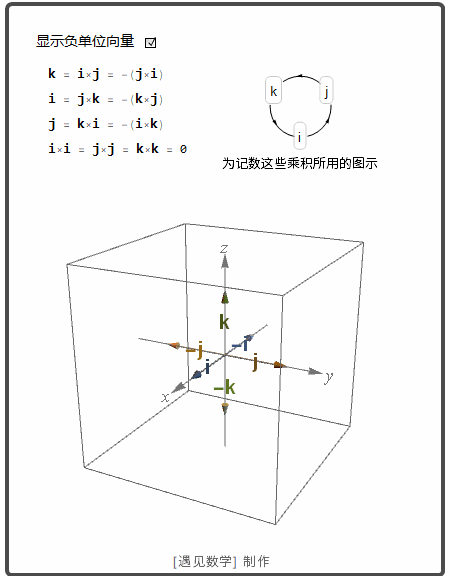
空间中两个向量的叉积

空间两个非零向量 u 和 v. 如果 u 和 v 不平行, 那么就确定了一个平面. 这样可以用右手法则选择一个垂直于这个平面的单位向量 n. |u×v| 是平行四边形的面积.

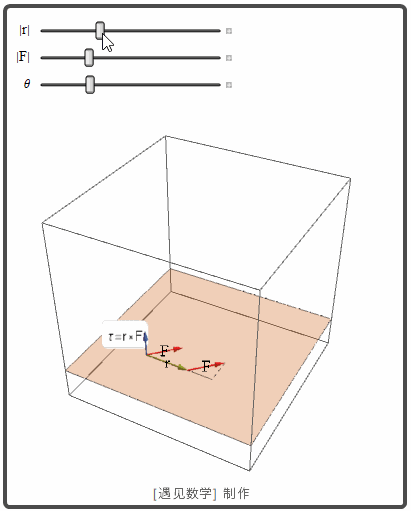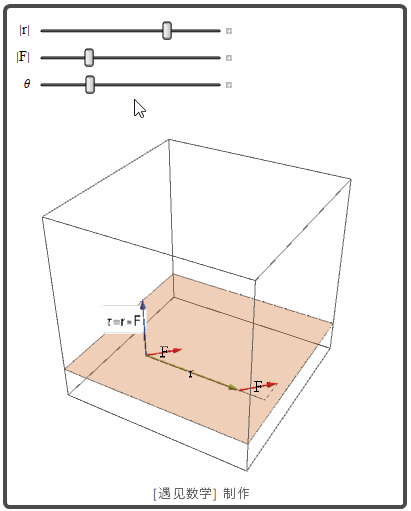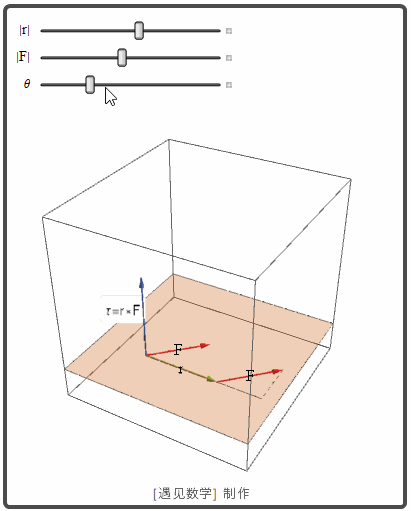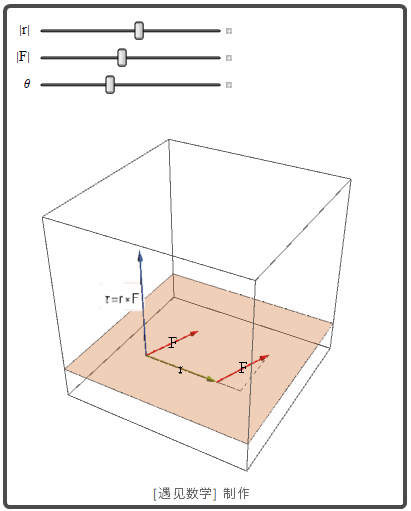
转矩(力矩, Torque)

当我们再扳手上用一个力 F 转动一个螺栓时, 就产生一个转矩作用在螺栓的轴上以使螺栓前进. 转矩的大小依赖力作用在扳手多远的地方和多大的在作用点垂直于扳手的力. 转矩的大小 τ 是杠杆 r 的臂长和 F 的垂直于 r 的数量分量的乘积

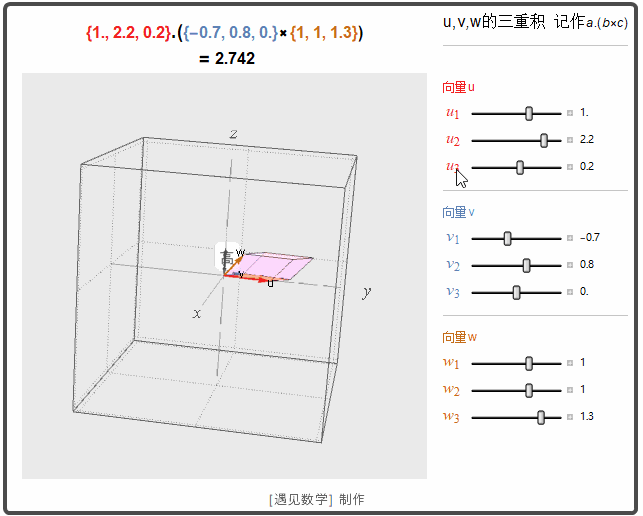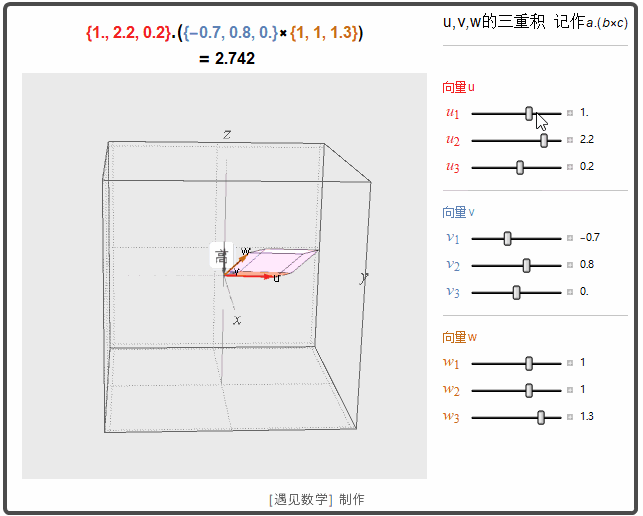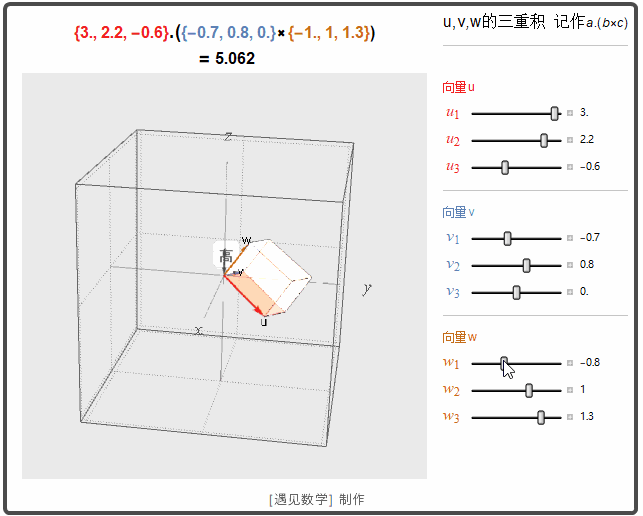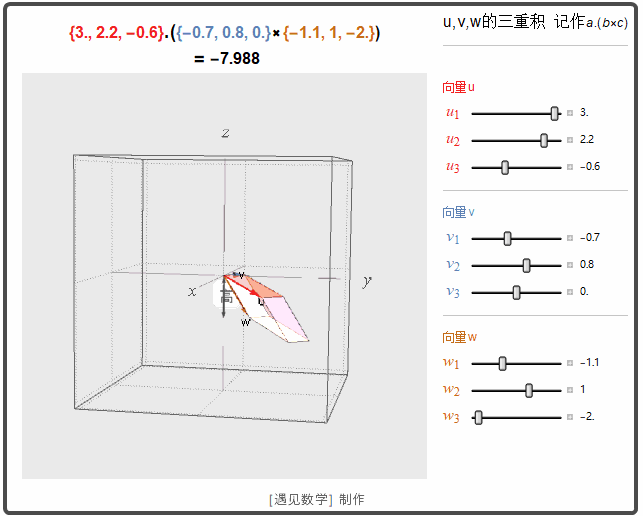
三重积

三重积，又称混合积，是三个向量相乘的结果。向量空间中，有两种方法将三个向量相乘，得到三重积，分别称作标量三重积和向量三重积.

「予人玫瑰, 手留余香」

转发既是支持, 我们会努力走得更远!