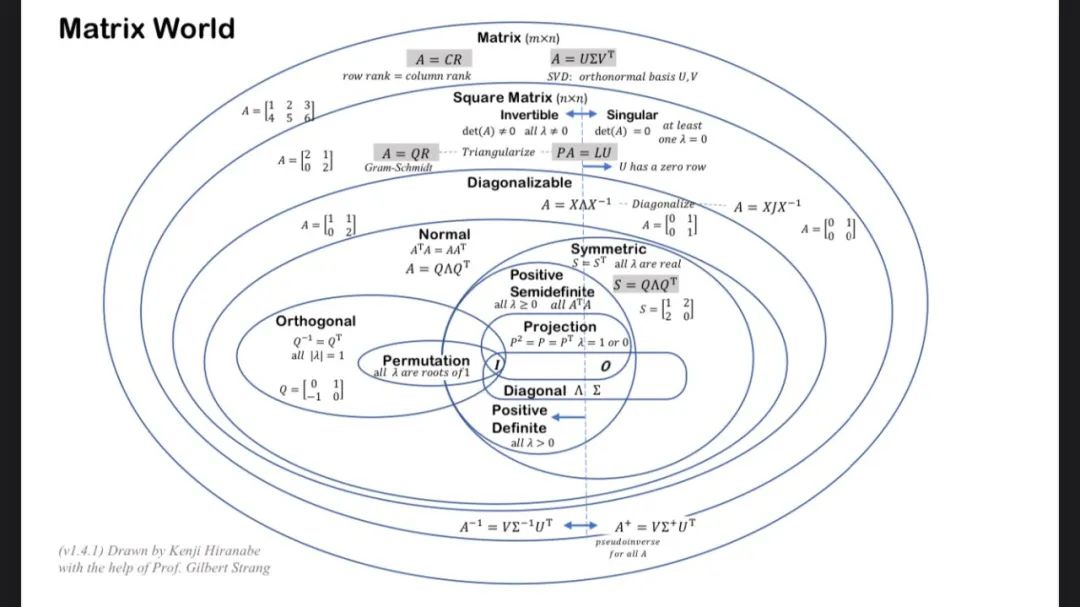
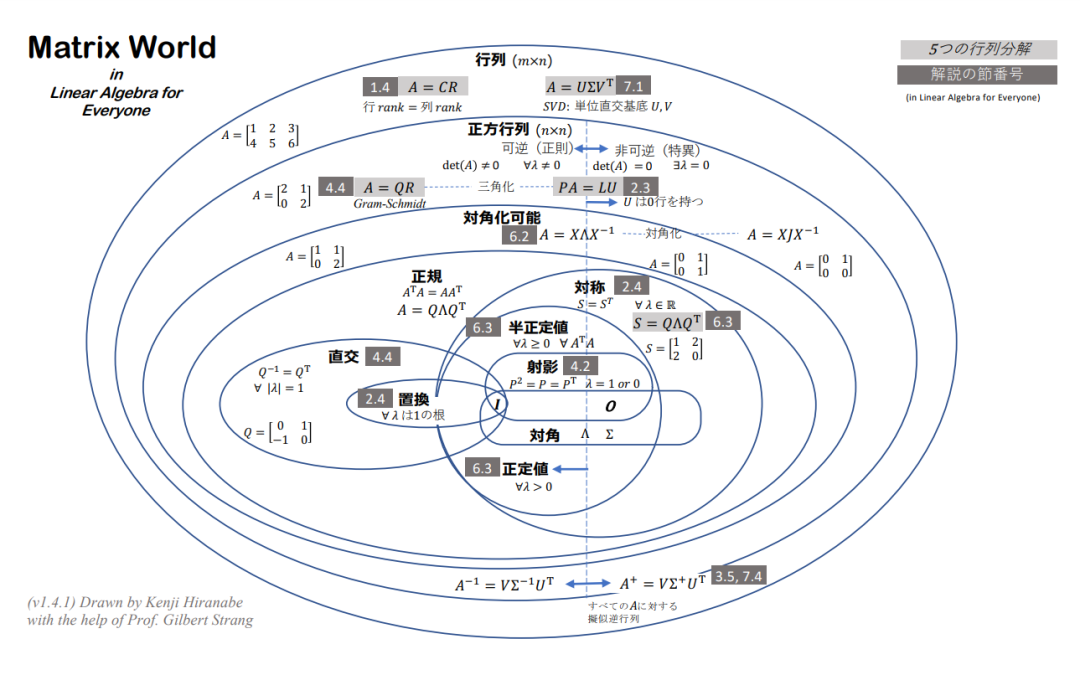
图文理解矩阵与线代！《矩阵世界与线性代数艺术》可视化手册，14页pdf，Kenji Hiranabe编著，Lecun点赞！

来自MIT Gilbert Strang教授的矩阵经典图解，收藏！

85岁MIT教授Gilbert Strang《线性代数》2020视频课，不怕学不会的线代

本笔记试着用直观的方式把《线性代数》中介绍的重要概念表达出来本课程旨在从矩阵分解的角度促进对向量/矩阵计算和算法的理解。它们包括列行(CR)、高斯消去(LU)、Gram-Schmidt正交化(QR)、特征值与对角化(QΛQT)和奇异值分解(UΣV T)。

https://github.com/kenjihiranabe/The-Art-of-Linear-Algebra

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“M14” 就可以获取《图文理解矩阵与线代！《矩阵世界与线性代数艺术》可视化手册，14页pdf，Kenji Hiranabe编著，Lecun点赞！》专知下载链接

                       

专知，专业可信的人工智能知识分发 ，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取100000+AI(AI与军事、医药、公安等)主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取100000+AI主题知识资料