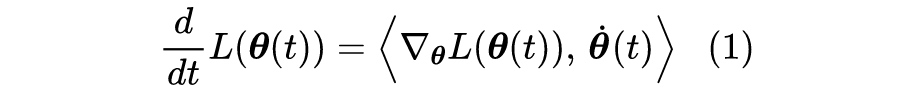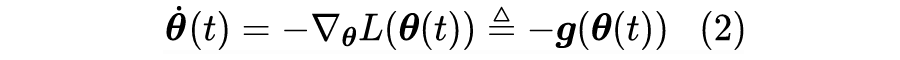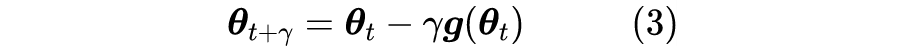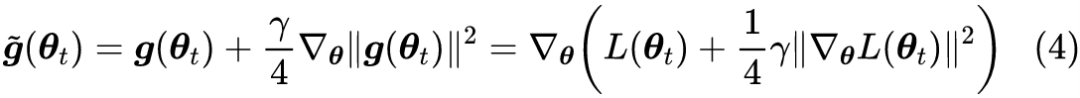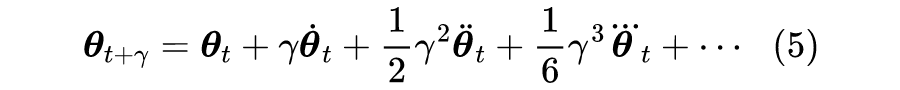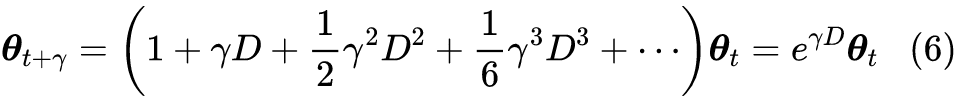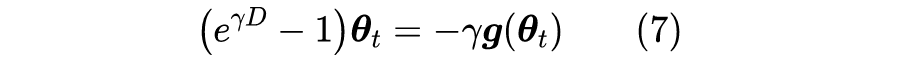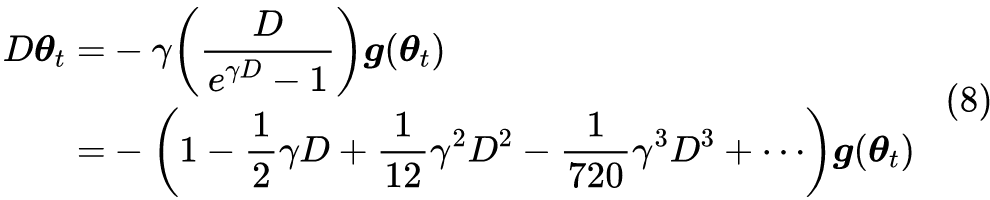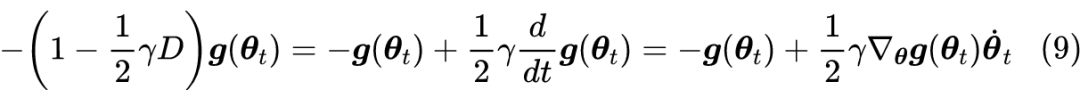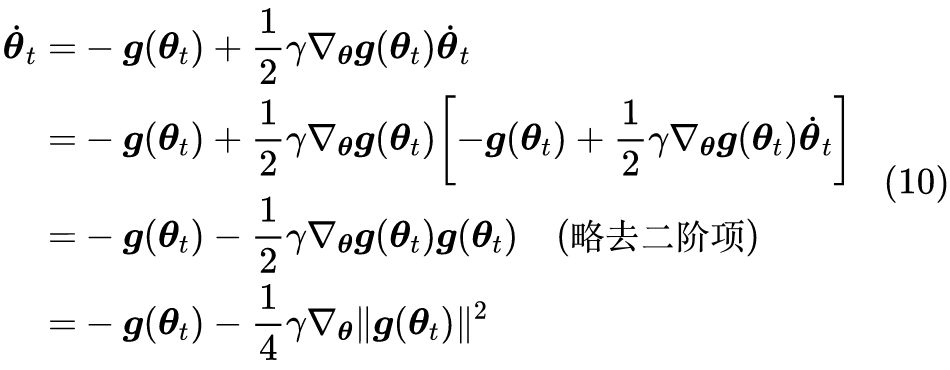从动力学角度看优化算法：为什么学习率不宜过小？

©PaperWeekly 原创 · 作者｜苏剑林

单位｜追一科技

研究方向｜NLP、神经网络

本文的主题是“为什么我们需要有限的学习率”，所谓“有限”，指的是不大也不小，适中即可，太大容易导致算法发散，这不难理解，但为什么太小也不好呢？一个容易理解的答案是，学习率过小需要迭代的步数过多，这是一种没有必要的浪费，因此从“节能”和“加速”的角度来看，我们不用过小的学习率。

但如果不考虑算力和时间，那么过小的学习率是否可取呢？Google 最近发布在 Arxiv 上的论文 Implicit Gradient Regularization [1] 试图回答了这个问题，它指出有限的学习率隐式地给优化过程带来了梯度惩罚项，而这个梯度惩罚项对于提高泛化性能是有帮助的，因此哪怕不考虑算力和时间等因素，也不应该用过小的学习率。

对于梯度惩罚，笔者已有过多次讨论，在文章对抗训练浅谈：意义、方法和思考（附 Keras 实现）和泛化性乱弹：从随机噪声、梯度惩罚到虚拟对抗训练中，我们就分析了对抗训练一定程度上等价于对输入的梯度惩罚，而文章《我们真的需要把训练集的损失降低到零吗？》[2] 介绍的 Flooding 技巧则相当于对参数的梯度惩罚。

总的来说，不管是对输入还是对参数的梯度惩罚，都对提高泛化能力有一定帮助。

降得最快的方向

该论文跟这个系列的文章一样，将优化过程看成是求解微分方程。回顾之前的文章从动力学角度看优化算法：一个更整体的视角，设损失函数为 ，我们将 看成是看成是沿着某种时间参数 t 变化的轨迹 ，现在我们考虑它的变化率：

我们希望 随着时间的变化是递减的（Loss 越小越好），所以希望上式小于 0，当模长 固定时，上式右端的最小值在梯度的反方向 取到，所以我们说梯度的负方向下降得最快方向。简单期间，我们可以直接令：

那么求解参数 就转化为求解上述常微分方程组，这也是“从动力学角度看优化算法”这个系列的基本出发点。

藏在学习率中的正则

然而，实际的问题是，我们没法真正去求解微分方程组（2），我们只能用数值迭代，比如采用最简单的欧拉法，得到：

这其实就是最朴素的梯度下降法，其中 也就是我们常说的学习率。上式本质上就是一个差分方程。

可以想象，从 出发，得到的点 与方程组（2）的精确解 会有一定的出入。

如何衡量出入到什么程度呢？不妨这样想象， 其实也是某个类似（2）的微分方程组的精确解，只不过对应的 换成了某个新的 ，我们比较 与 的差异就好了。

经推导，如果仅保留到 的一阶项，那么有：

推导过程我们放在下一节。可以看到，其实就相当于往损失函数里边加入了梯度惩罚形式的正则项 ，而梯度惩罚项有助于模型到达更加平缓的区域，有利于提高泛化性能。

这也就是说，离散化的迭代过程隐式地带来了梯度惩罚项，反而是对模型的泛化是有帮助的，而如果 ，这个隐式的惩罚则会变弱甚至消失。

因此，结论就是学习率不宜过小，较大的学习率不仅有加速收敛的好处，还有提高模型泛化能力的好处。当然，可能有些读者会想，我直接把梯度惩罚加入到 loss 中，是不是就可以用足够小的学习率了？理论上确实是的，原论文将梯度惩罚加入到 loss 中的做法，称为“显式梯度惩罚”。

差分方程到微分方程

对于差分方程到微分方程的转换，我们可以用普通的“摄动法”来求解，笔者也有过简单介绍（可以查看标签“摄动” [3] ）。不过更漂亮的解法是直接利用算符的级数运算来做，参考之前的文章《算符的艺术：差分、微分与伯努利数》[4] 。

我们用泰勒级数展开 ：

如果将对 t 求导的运算记为 D，那么上式实际上是：

所以差分方程（3）可以写为：

跟常规的代数运算一样，我们有：

等号左端就是 ，因此等号右端就是 的表达式了，保留到一阶项为：

也就是：

所以一阶的 ，推导完毕。

例行公事的小总结

深度学习的发展和普及离不开基于梯度下降的优化器的成功应用，而梯度下降为何能如此成功，依然还没得到深刻的解释。众多研究人员在“炼丹”过程中，多多少少也能总结出一些不知道为什么有效的“奇技淫巧”出来，诸如 batch_size 该取多大、学习率该怎么调，估计每个人也有自己的经验。

对于“学习率不能过小”这个现象，大家应该都有所体会，很多时候可能已经默认作为一个“常识”使用，而懒得思考背后的原理了。

Google 的这篇论文则为理解这个现象提供了一个可能的解释：适当而不是过小的学习率能为优化过程带来隐式的梯度惩罚项，有助于收敛到更平稳的区域。笔者认为其分析过程还是值得参考学习的。

参考文献

[1] https://arxiv.org/abs/2009.11162

[2] https://kexue.fm/archives/7643

[3] https://kexue.fm/tag/%E6%91%84%E5%8A%A8/

[4] https://kexue.fm/archives/3018

更多阅读

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

📝 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

📬 投稿邮箱：

• 投稿邮箱：hr@paperweekly.site 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。