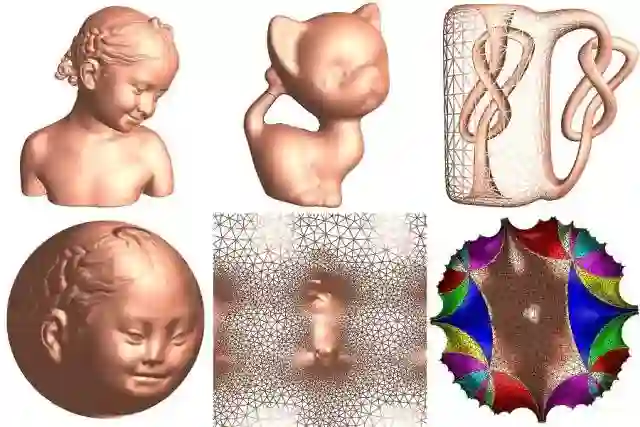
超越时代的眼光 - 为丘成桐先生七十寿辰而作
本文经授权转载自《老顾谈几何》微信公众号
【2019年3月22-24日,清华三亚人工智能高端论坛将在三亚市召开。23日下午,5:40-6:10pm,老顾将介绍和丘成桐先生的近期工作“最优传输观点下的对抗生成模型”,包括用蒙日-安培方程正则性理论来解释模式崩溃问题。敬请光临指导。 】
老顾的童年生长在经济文化相对落后的东北,母亲家族世代生活在医巫闾山脚之下。医巫闾山上碑刻摩崖星罗棋布,古刹殿堂云雾缭绕。每年梨花绽放时节,遍山浸透“香雪海”。医巫闾山的望海峰顶,坐落着契丹辽国太子耶律倍的读书堂,这里一度是契丹王朝的文化中心。千年之后,医巫闾山脉草莽出没,迷信横行。童年时,父母经常哀叹辽地科学落后,文化不兴。那时冬日晚上,寒风呼啸,滴水成冰,电视尚未普及,族人亲戚经常聚在一起,谈古论今,讲述充满萨满风情的民间传说。父辈们都认为世间存在着一些世外高人,他们开了天眼,通晓天地玄机,洞悉历史未来,领悟了宇宙奥义,超越了世俗生死。那时契丹佛教文化早已烟消云散,但是女真萨满文化仍有留存。当地民间传说中依然记得这样一位世外高人,耶律楚才。耶律楚才通天文地理,律历术数,以及释老医卜,曾经辅佐成吉思汗、窝阔台,为留存推广汉家文化,做出不可磨灭的贡献。童年时,父母亲戚教导老顾少年时要壮游天下,追随世外高人,努力习得真知灼见。
数十年后,老顾回顾求学生涯,觉得此生的确有幸遇到世外高人:丘成桐先生。丘先生的先祖可能为躲避成吉思汗的铁蹄,南下闽粤,成为客家人。丘成桐先生童年贫寒却壮志凌云,苦学不辍,终开天眼,将微分几何和偏微分方程融为一炉,创立几何分析学派,在数学领域开天辟地,震烁古今!丘先生证明过一系列猜想,气魄恢弘,雷霆万钧!其中卡拉比-丘成桐流形揭示了宇宙间最为幽深的奥秘,解释了基本粒子的本源规律。仓颉造字而夜鬼哭,卡丘流形而上帝惊!当年小顾远渡重洋,来到哈佛大学,拜在丘先生门下,承蒙丘先生不嫌小顾学识粗浅,蒙昧愚钝,将小顾收留并悉心教导。那时小顾慧根不够,冥顽幼稚,无法领悟丘先生教授的天机。现在回想,依然懊悔不迭。但是在丘先生的指导下,在几何分析门派的熏陶下,老顾多少有一些亲身经历和人生体悟。在丘先生超越时代的目光注视下,老顾竭尽所能将几何分析的思想推向实践应用。
目前丘成桐先生众多弟子中,只有老顾同时在数学和计算机科学领域进行研究。因此,在数十年的学术生涯中,老顾能够具有与众不同的视角,看到独特奇妙的风景,更有难以言传的洞察和一言难尽的体验。在过去的数十年中,老顾目睹了丘先生所创立的几何分析学派高歌猛进,不断揭示大自然瑰丽雄奇的秘密。特别是证明庞加莱猜想的黎奇曲率流方法更加体现了几何分析方法的博大精深、强悍有力。另一方面,计算机科学彻底革命了人类社会,接踵而至的各种技术浪潮,深刻地改变着人类的经济模式、社交方式和思维范式。丘先生认为基础科学的突破影响深远,是人类文明的真正推动力量,但是,绝大多数的芸芸众生囿于所处的社会环境和历史局限,很难充分认识并且有机会践行这一点。作为计算机科学家,老顾不懈地追逐每一个技术浪潮,力图在每一次浪潮中寻求具有根本重要性的基础问题,用丘先生教授的几何分析手法加以解决。老顾一直梦想着将几何分析的光辉思想在计算机技术中发扬光大,从而将阳春白雪介绍入寻常百姓家,从物质层面为人类文明做出力所能及的些许贡献。
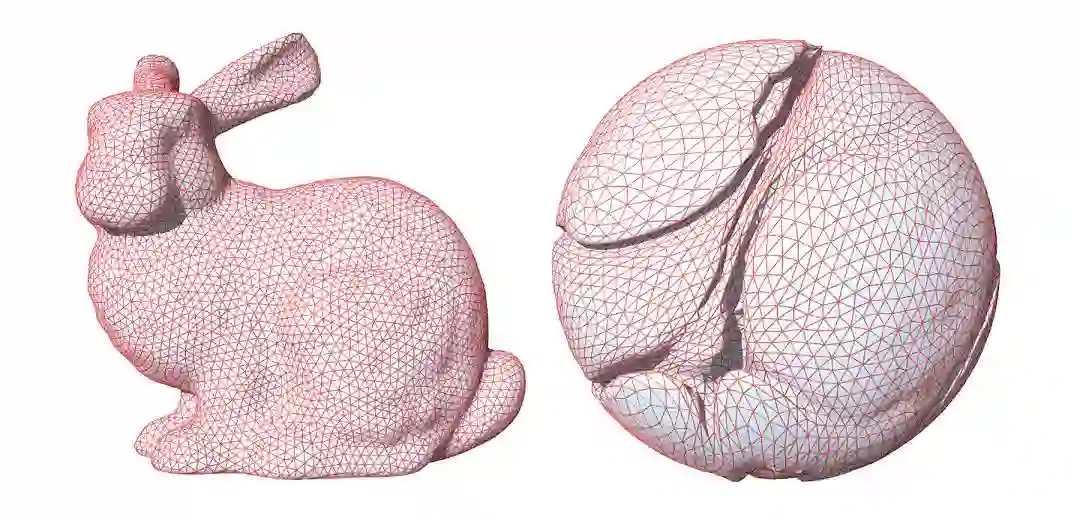
图1. 曲面参数化。
公元两千年左右,恰是计算机图形学飞速发展的时代,基于物理的渲染计算模型成熟,数字几何这一分支领域开始独立,动漫游戏工业蓬勃发展。最为显著的标志就是昂贵的专用图形工作站被廉价的图形加速卡所取代,特别是纹理贴图的技术极大地提高了渲染算法的质量、提高了计算机生成图像的逼真程度。纹理贴图依赖于曲面参数化技术,这一技术本质上等价于计算曲面到平面区域之间的微分同胚,同时尽量减小几何畸变。当时黎曼映照被用于拓扑简单曲面的参数化,但是这种方法无法处理拓扑复杂曲面。那时,丘先生教会了老顾阿提亚-辛格指标定理:黎曼流形上椭圆形偏微分方程解空间的维数由流形的拓扑所决定。具有黎曼度量的可定向曲面都是黎曼面。在黎曼面情形,指标定理就是黎曼-罗赫定理。对于曲面全局参数化,我们的算法本质上是在计算全纯一次微分(holomorphic one form)。当时,丘先生深入浅出地给老顾讲解了这一理论的所有细节,酣畅淋漓,深邃精妙。老顾感悟到了这一理论美轮美奂,也想像到了巨大的实用价值。深刻理解了抽象理论之后,转化成算法就自然是水到渠成。很快老顾实现了计算机算法,这或许是人类历史上首次全纯微分形式显示在计算机屏幕之上。一旦抽象的黎曼面概念变成了通用算法,其应用的范围就远非其发明者所能想象。当时数字几何领域的计算机科学家对于全纯微分的概念并不了解,无法给与这一算法恰如其分的评价,致使这一发明受到冷遇。当时老顾年轻气盛,满腔热情受到现实挫折后,变得愤世嫉俗。其实,那时也有很多学者具有远见卓识,对于这一横空出世的算法秉持支持欣赏态度。
图2. 全纯微分形式诱导的叶状结构。
数年后,依随核磁共振和计算机断层扫描技术的成熟,医学图像浪潮兴起。CT图像用于直肠癌筛查。由于肠壁曲面具有很多皱褶,隐藏其间的息肉难以被查出。老顾和合作者们提出将直肠曲面摊开展平的想法,并用全纯微分的方法加以实现,这成为虚拟肠镜技术的一个核心。很快基于全纯微分方法的虚拟肠镜算法专利被转让给西门子和GE公司,成为他们CT扫描设备配套软件的标配。十数年后,无论老顾走到任何一个城市,如果和当地医院的放射科医生攀谈,都会谈到虚拟肠镜。前些天老顾和友谊医院的大夫讨论,他主动演示了虚拟肠镜的实例,看到平展在屏幕上的直肠曲面,老顾顿觉释然:全纯微分形式终于以丘先生和老顾意想不到的方式在全世界普及开来,借助虚拟肠镜的应用而家喻户晓。相信这一抽象的黎曼面概念和几何分析的方法已经在全世界拯救过不少的生命,而这一切都来自于丘先生办公室中的那块黑板。那天午后,凭借这块黑板,丘先生教会了老顾上同调群、调和微分形式、霍奇分解、全纯微分等玄而又玄的概念。哪里想到多年之后,天下有医院处,就有几何分析,就有全纯微分。
图3. 虚拟肠镜。
那时候,每个周末都会从纽约飞来一位教授,俊逸潇洒,风流倜傥。一双明眸,深情诚挚,直达心底,令异性无法抗拒。这就是后来名满天下的哈密尔顿先生(Richard Hamilton),黎奇曲率流的发明人。哈密尔顿先生和丘先生每个周末都夜以继日、通宵达旦地讨论如何用黎奇流证明庞加莱猜想。老顾也在那个阶段学习了黎奇流的相关理论知识。丘先生一直认为构造具有特殊性质的黎曼度量在微分几何中具有中心的地位。老顾后来在工程领域的研究生涯中,真切地验证了这一真知灼见。计算机视觉、医学图像领域中的曲面配准、形状识别、几何归类本质上都和构造标准黎曼度量有关。而黎奇流是构造黎曼度量的不二法门。虽然随着庞加莱猜想的证明完成,黎奇流的理论日臻完美,黎奇流的离散理论尚未发展成型。老顾和合作者们经过多年努力,最终建立了离散曲面黎奇流的严格理论,发展出实用的算法。走在曼哈顿街头,高楼林立,行人如织,在老顾看来都是各色曲面,在黎奇流下万宗归一,都会变形成具有常曲率黎曼度量的曲面。宛如《骇客帝国》中的Neo走在矩阵(Matrix)之中,觉得世间万物皆为代码,曼哈顿街头的老顾也经常觉得眼前一切幻像,背后必有永恒的真实,因而经常物我两忘,神游天外。相比于全纯微分形式,黎奇流更为广泛深刻,普适有力。虽然人们依然没有意识到这一方法的潜在价值,老顾深信未来会有一天,黎奇流也会以令人难以想象的方式普惠天下。
图4. 黎奇曲率流计算的标准黎曼度量。
依随时代的发展,当下以深度学习为代表的人工智能掀起狂潮。这一浪潮对于传统的科学哲学带来了前所未有的冲击。深度学习用相关性替代因果律,用经验公式替代理论体系,很多学者主张用计算蛮力取代深刻理解。主流的观点认为人工的特征筛选无法和机器的端到端学习相匹敌。传统的拓扑几何、偏微分方程迅速成为冷门,年轻一代将巨大的热情和精力投入到永无止境的调参中去。在一片喧嚣中,老顾依然坚持从丘先生那里学来的治学方法:用严密的数学来分析事物的本质,用几何观点来理解深度学习的方法。老顾倾向于认为数据具有内在的模式,模式可以用高维数据空间中低维流形上的概率分布来描述。深度学习方法能够隐式地发现流形的结构,同时实现概率测度变换。而概率测度变换可以由多年前丘先生教给老顾的蒙日-安培方程理论来理解。
图5. 蒙日-安培方程方法计算的最优传输映射。
1995年,老顾刚到哈佛大学,在麻省理工选修“机器视觉”课程。当时Horne教授提出基于闵可夫定理的曲面表示方法。当时老顾求教于丘先生,丘先生给老顾讲解了蒙日-安培方程理论,特别是基于亚历山大定理的几何求解方法。丘先生也给老顾讲解了蒙日-安培方程解的正则性理论,提到了汪徐家教授的定理。当时老顾只体会到这些定理的美学价值,但是并没有意识到如此深邃的理论会有朝一日直接应用到工程领域。在数十年的计算机科学领域的学术生涯中,老顾从来没有看到过任何研究工作是基于偏微分方程解的正则性理论。但是,出乎意料的事情再度发生。近几年来,深度学习中的对抗生成网络方法如日中天,但是这一方法的训练相对困难,系统对于超参数异常敏感,经常出现所谓的模式崩溃的现象。老顾团队认为对抗生成网络的一部分计算是用于概率测度变换,这一变换和蒙日-安培方程的解密切相关。由正则性理论,概率变换映射通常是非连续变换,而深度神经网络只能表达连续映射,这一内在矛盾解释了深度学习的内在困难,例如模式崩溃。令人意外的是,经过多年的蛰伏,二十五年前学习的理论居然成为解决时下热门问题的关键;在最为反传统的时髦领域,根本问题的解决之道在于最为传统的理论。依据蒙日-安培方程的亚历山大定理,老顾的团队提出了新颖的计算框架,这一框架非常适合硬件实现,期待基于这一理论的AI芯片早日出现。
图6. 模式崩溃的几何解释。
回顾过去的历史,老顾看到几何分析的思想和方法在计算机科学发展的每一个浪潮都大有用武之地,对于很多领域根本问题的理解都有独到的观点,提出了卓有成效的解决方法。虽然计算机技术的发展日新月异,但是它们依然是根植于基础数学。丘先生数十年前教授给老顾很多几何分析的方法,领先于时代,在当时的技术水平下无法充分发挥其内在的潜力;数十年后这些抽象的概念和思想逐渐被转化成计算机算法,日益渗透到社会生活之中。
童话中的世外高人的确行走于人间,那些开了天眼之后洞察的自然奥秘,经过刻苦学习之后可以被天资平庸之人所领悟。能够师承丘先生,老顾一直觉得三生有幸。全纯微分形式、黎奇流、标准黎曼度量、蒙日-安培方程等等,丘先生传授的这些基本概念和思想成了老顾生命中的压舱石,令老顾时刻警醒,免于浮躁,超脱喧嚣。行走于红尘之中,飘忽于天地之间,老顾无时不刻体会到超越于生命之外的永恒。
丘先生有一次告诉老顾,宇宙是高维的,时空的每一点都有一个卡拉比-丘流形作为纤维,在未来,这些纤维将会成为星际旅行的关键。我们由衷希望在丘先生九十寿辰之际,这一梦想成为现实!
【2019年3月20日清晨,写于上海浦东机场。】