【速览】ICML2022 | 深入浅出探究置换敏感的图神经网络
学会“成果速览”系列文章旨在将图像图形领域会议期刊重要成果进行传播,通过短篇文章让读者用母语快速了解相关学术动态,欢迎关注和投稿~
◆ ◆ ◆ ◆
ICML2022:深入浅出探究置换敏感的图神经网络
*通讯作者:何晖光
◆ ◆ ◆ ◆
图与邻接矩阵的置换不变性是图神经网络(GNNs)的首要要求,传统模型通过置换不变的聚合操作来满足这一前提条件。然而,这种置换不变的方式可能会忽略邻居与邻居之间的相互关系,进而阻碍GNN的表达能力。为了解决这一问题,本工作利用置换群(permutation groups)设计了一种新颖的置换敏感聚合机制,通过置换采样捕获邻居与邻居之间的二元依赖(即成对相关性),从而高效地提升GNN的表达能力:我们证明了所提出的方法严格地比二维Weisfeiler-Lehman(2-WL)图同构测试更强大,并且能够区分一些3-WL测试无法区分的非同构图对;此外,相比于传统方法完全考虑所有n!种置换,我们所提出的方法实现了线性的置换采样复杂度。
综合而言,本工作基于置换敏感的聚合机制设计了一种强大而高效的图神经网络,它在保证表达能力的同时,先后借助近似置换不变性的思想与线性置换采样策略,显著降低了计算复杂度。在多个合成数据集和真实数据集上的大量实验验证了所提出模型的优越性。
图与邻接矩阵的置换不变性是图表示学习中一个关键的归纳偏置。先前的许多研究[1-4]都致力于设计置换不变的聚合函数,以使得图神经网络(GNN)整体对于结点的顺序置换不变(输入图中结点的置换不影响输出结果)或置换等变(输入图中结点的置换使得输出结果随之一同置换)。
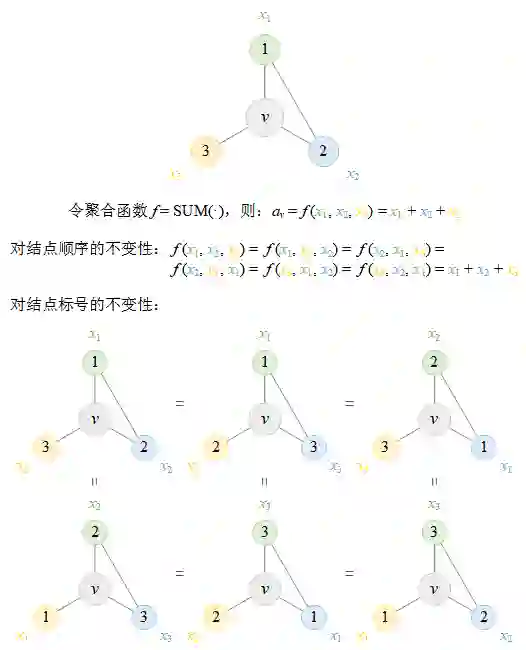
此处我们提供了一个简单示例来帮助读者更好地理解置换不变性。如图1所示,假设我们考虑一个具有中心结点v和3个邻居结点的图。置换不变的聚合函数,例如广泛使用的求和函数SUM(•),对于结点的任意置换都将输出相同的结果。
图 1 置换不变聚合函数SUM(•)的置换不变性
然而,置换不变聚合函数的这种强对称性假定所有邻居结点的地位均等,忽视了邻居结点与邻居结点之间的相互关系。下图2展示了位于中心结点v的置换不变聚合函数所能感知到的拓扑结构,中心结点v只能意识到邻居结点的存在、但无法区分任意两个邻居结点之间是否存在连接,进而无法识别和重建图中细粒度的子结构,只能够重建出最简单的“星形”子结构(这与[5]中的结论一致)。因此,这种置换不变的聚合方式可能会阻碍GNN的表达能力。
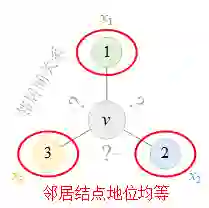
图 2 置换不变的聚合函数只能感知到“星形”的拓扑结构
下图3展示了一对非同构图,大多数置换不变的聚合函数都无法区分它们:无论经过多少轮聚合(迭代),置换不变的聚合函数对于这两个图总是输出相同的结点特征(分布),因此误认为它们是相同的图,进而无法区分。
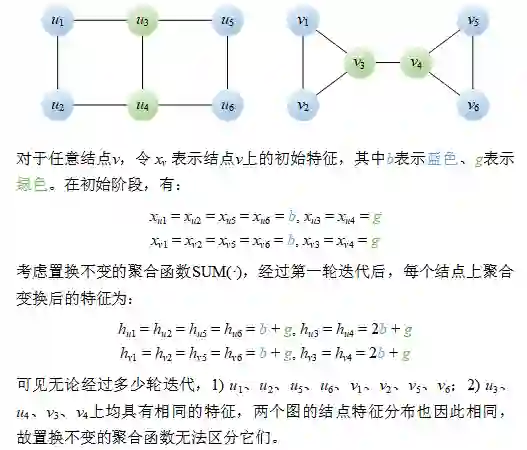
图 3 常见的置换不变聚合函数无法区分的一对非同构图
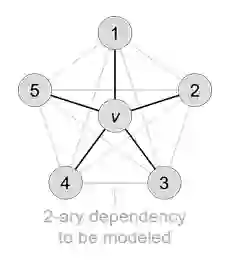
与置换不变相反,置换敏感的聚合函数对于结点顺序非常敏感,可以看作是一种“对称性破缺”机制,打破了邻居结点的均等地位。这样一来,聚合函数可以显式地建模邻居结点之间的内在关系(如二元依赖)。如图4所示,这种二元依赖关系帮助捕获两个邻居结点之间是否存在连接,从而利用局部的图子结构来提高表达能力。
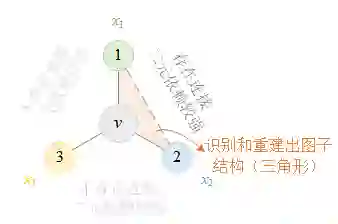
图 4 置换敏感的聚合函数所感知到的拓扑结构
同样对于这对非同构图,注意到u3的邻居之间没有任何连接,但v3的邻居v1和v2之间存在连接。因此,置换敏感的聚合函数可以利用二元依赖捕获该连接(以及三角形子结构)。仅经过第一轮聚合(迭代)后,置换敏感的聚合函数就能够输出不同的结点特征(分布),从而成功地区分它们。
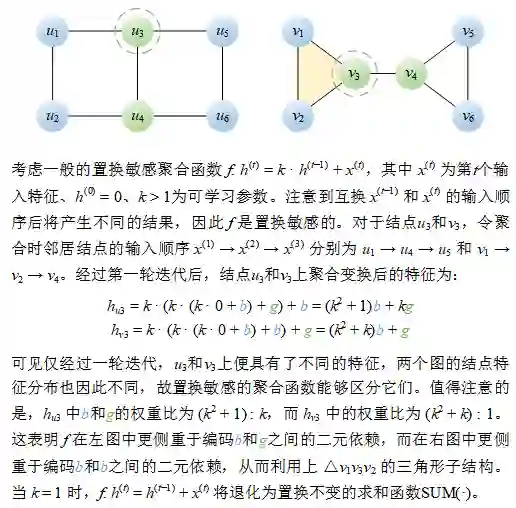
图 5 一般的置换敏感聚合函数能够区分的一对非同构图
实际上,在经过足够的采样之后,置换敏感的聚合函数能够计数每个结点上的三角形数量。我们在文中提出了以下定理,从三角形计数的角度解释了为何一般的置换敏感聚合函数具有更加强大的表达能力。
尽管置换敏感的聚合函数比置换不变的聚合函数具有更加强大的表达能力,然而却面临着计算复杂度的巨大挑战。为了保证GNN整体的输出结果对于输入结点的置换严格不变,置换敏感的聚合函数需要考虑所有n!种可能的结点排列(置换),从而导致了极高的计算复杂度。这种复杂度上的巨大缺陷进一步限制了它们在实践场景中的广泛应用。下图6以3个邻居结点为例,展示了如何通过考虑所有3! = 6种置换来保证模型整体的置换不变性。
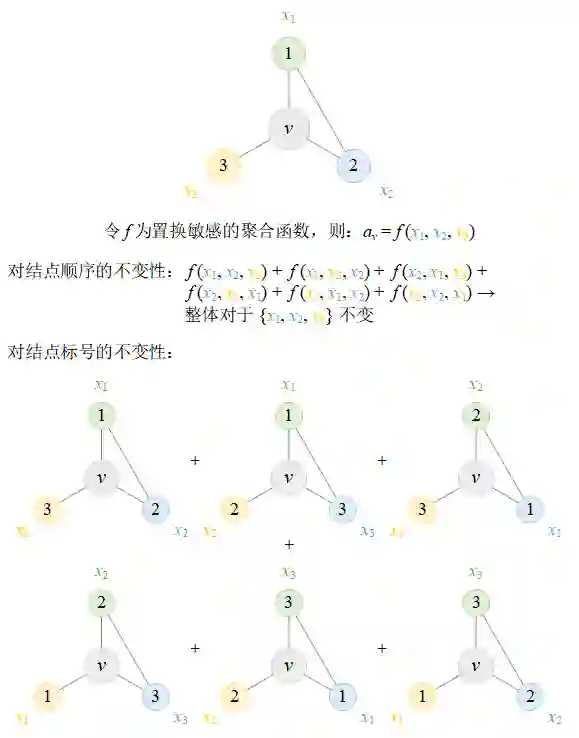
图 6 置换敏感的聚合函数需要考虑所有n!种置换来保证整体的置换不变性
为此,我们提出以下思路来应对计算复杂度的挑战:
我们建议近似置换不变性而非严格保证置换不变性,以避免考虑所有n!种结点排列(置换)。例如,我们可以对所有二元依赖进行建模,以确保对二元依赖的不变性,从而通过对二元依赖的不变性来近似置换不变性(对
此外,我们还设计了一种高效的置换采样策略,实现了以最低的置换采样复杂度(即最少数量的置换)覆盖所有二元依赖。借助这种策略,可进一步将置换采样的复杂度从
随后将以下图为例,详细解释所提出的置换采样策略。
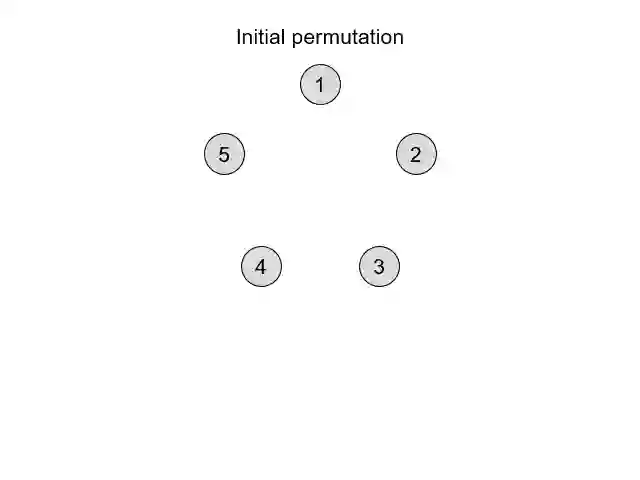
如图所示,假设我们考虑一个具有中心结点
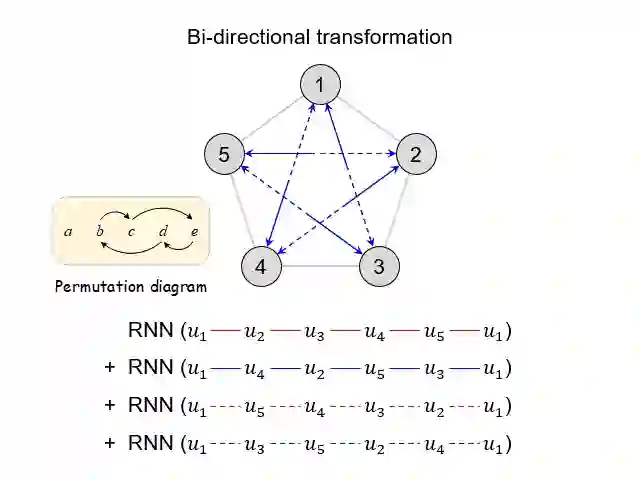
我们使用自然顺序1~5作为结点的初始排列、并在排列结尾对首个结点“1”重复一次,即“1-2-3-4-5-1”;随后利用置换敏感的循环神经网络(RNN)对其进行建模,同时覆盖5个二元依赖。下图中每条边表示已建模/覆盖相应的二元依赖,整体对应于一个哈密顿圈(Hamiltonian cycle,经过图中每个顶点恰好一次的圈)。
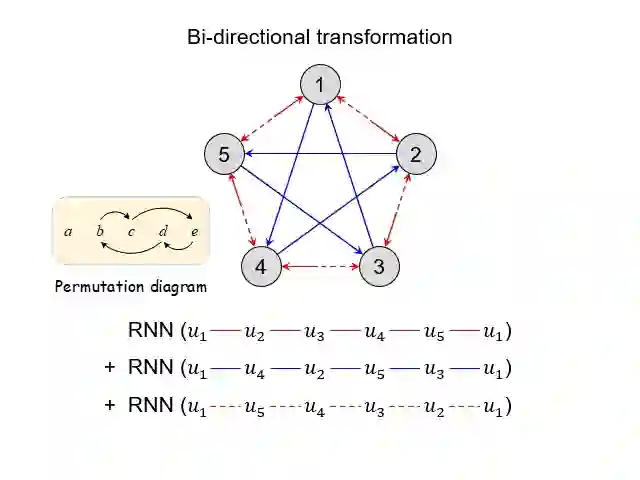
接下来,我们基于置换群(permutation group)及群作用(group action)生成新的排列。为了使得置换采样策略通俗易懂,此处我们简化了有关群论的复杂概念,仅根据“Permutation diagram”(置换示意图)展示如何通过置换初始排列来生成新的排列。置换示意图中的有向弧b → c表示将b移动到c的原始位置。生成与建模新排列的整个过程如以下动画所示。
由于在置换敏感的函数中,输入顺序a → b和b → a会导致不同的结果,因此这些二元依赖和边都是以有向的方式进行建模。我们继续根据置换示意图置换上一个排列,从而生成一个新的排列,并相应地建模一个反向的(红色)哈密顿圈。
经过双向建模后,可将红色哈密顿圈中的有向边转化为灰色的无向边。
最后一个蓝色哈密顿圈的反向建模及无向转换与之前类似。
以下动画对上述步骤进行了汇总,展示了所提出置换采样策略的完整过程。
简而言之,我们采样少量具有代表性的置换,进而生成相应的结点排列来覆盖所有二元依赖,并利用置换敏感的聚合函数来建模这些排列以及所覆盖的二元依赖,形成了一种新颖的置换敏感聚合机制;另一方面,我们通过对二元依赖的不变性来近似置换不变性。这样一来,既可以保证模型的表达能力,又能够在确保一定泛化能力的前提下显著降低计算复杂度。
置换敏感的图神经网络比置换不变的图神经网络更加强大,它们能够建模邻居结点之间的内在关系(如二元依赖),进而计数图中的子结构。
对于大多数图相关的任务,没有必要严格保证置换不变性。对于置换不变性的良好近似(例如,对二元依赖的不变性)可以显著降低计算复杂度,同时有效地保证泛化能力。
所提出的置换采样策略实现了线性的置换采样复杂度,达到了理论下界,有望应用于更广泛的GNN设计中。
综上所述,本工作探讨了为什么置换敏感的聚合函数能够提高GNN的表达能力。随后基于置换敏感的聚合机制设计了一种强大而高效的图神经网络,它在保证表达能力的同时,先后借助近似置换不变性的思想与线性置换采样策略,从而显著降低了计算复杂度。如何利用置换敏感的图神经网络在表达能力上的天然优势,在表达能力和计算复杂度之间寻找均衡,将是未来富有前景的研究方向。
[1] Duvenaud D K, Maclaurin D, Iparraguirre J, et al. Convolutional networks on graphs for learning molecular fingerprints. In Advances in Neural Information Processing Systems, 2224-2232, 2015.
[2] Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks. In International Conference on Learning Representations, 2017.
[3] Gilmer J, Schoenholz S S, Riley P F, et al. Neural message passing for quantum chemistry. In International Conference on Machine Learning, 1263-1272, 2017.
[4] Xu K, Hu W, Leskovec J, et al. How powerful are graph neural networks? In International Conference on Learning Representations, 2019.
[5] Chen Z, Chen L, Villar S, et al. Can graph neural networks count substructures? In Advances in Neural Information Processing Systems, 10383-10395, 2020.