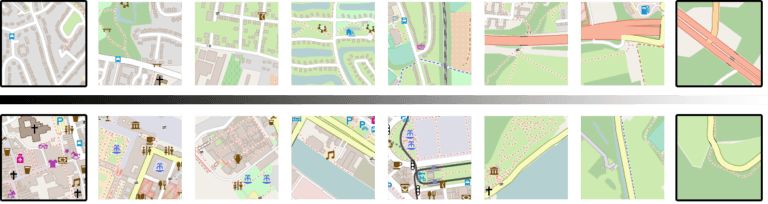
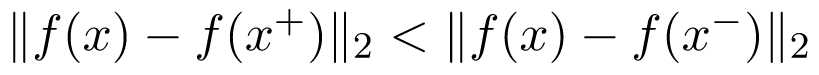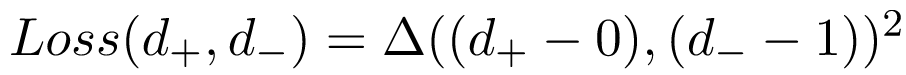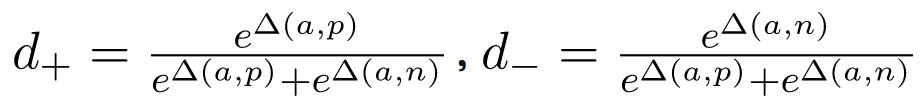Loc2Vec 基于三重损失学习位置嵌入

来源：sentiance.com

编译：weakish

编者按：Sentiance首席数据科学家Vincent Spruyt介绍了如何基于CNN和三重损失函数，学习位置嵌入。

在Sentiance，我们开发了一个平台，从智能手机感知数据（加速度传感器、陀螺仪、位置信息等）中提取行为学的洞见。我们的AI平台学习用户模式，能够据此预测和解释事件何时、为何发生，让我们的客户能够更好地辅助其用户，在合适的时间，以合适的方式接触用户。

这一平台的一个重要组件是地点映射算法。地点映射的目标是根据位置测量得出当前访问的地点，位置测量来自智能手机的位置子系统，经常不够精确。

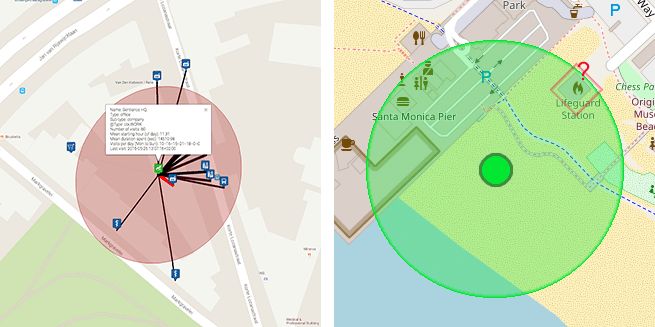
左：估计用户实际访问的相邻地点；右：快速丢弃可能性不大的地点，例如海滩上的救生站

尽管地点映射本身就是一个困难的问题，足以专门写一篇博客，人类的直觉能在很大程度上帮助解决这一问题。考虑上图中访问圣莫尼卡海滩的例子。稍微一瞥周边地点，就能得出结论，用户真去访问一个救生站的几率大概非常小。

事实上，仅仅只是查看某一区域的地图，人类常常能够快速丢弃可能性不大的地点，并形成关于实际发生的情况的先验信念。地点在工业区，公园，海滩旁，市中心，公路旁？

为了在我们的地点映射算法中加入类似的直觉，我们开发了一个基于深度学习的方案，经训练后可以编码地理空间关系和语义相似性，描述位置的周边。

编码器输出的嵌入捕捉了输入位置的高层语义

编码器转换位置为分布表示，类似用于自然语言的Word2Vec。这些嵌入位于一个度量空间之中，因而遵循代数规则。以词嵌入为例，我们可以推断单词相似性，甚至直接在嵌入空间中进行算术运算，例如“国王 - 男人 + 女人 = 王后”。

接下来我们将讨论，如何设计一个方案，将位置坐标映射至让我们可以进行类似操作的度量空间。

图块生成

栅格化GIS数据

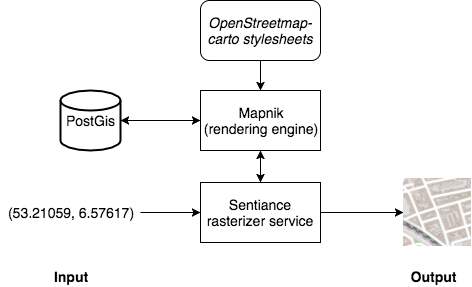
给定位置的坐标和半径，我们可以查询GIS数据库获取大量地理信息。我们的GIS数据库是OpenStreetMap的本地拷贝，存储在PostGis数据库中。PostGis是PostgreSQL的一个方便的扩展，增加了空间操作、类型、索引支持。

例如，使用一组查询语句，我们很容易就可以检查位置附近是否有河流，到最近的火车站有多远，位置是否靠近马路。此外，道路本身可以作为多段线获取，而火车站建筑的轮廓也许能以多边形对象的形式提供。

然而，神经网络难以高效地处理这些未结构化的大量数据。考虑到我们的目标是训练神经网络理解形状和空间关系，例如距离、包含、封闭、除外，我们决定栅格化位置周边，得到固定尺寸的图像，再传入编码器。

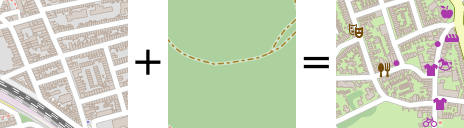
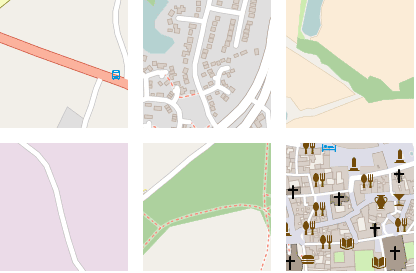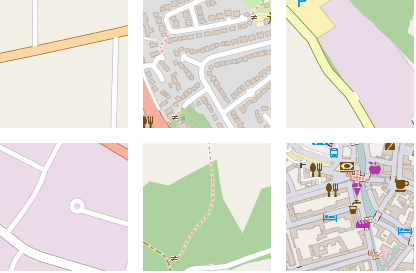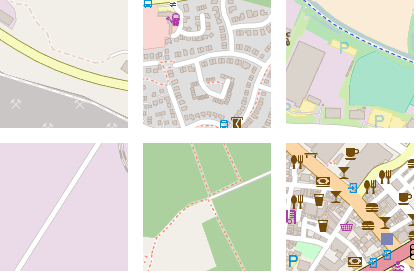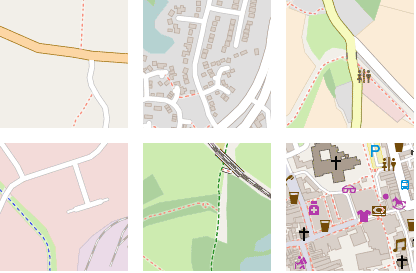
幸运的是，这些有很高效的现成工具。我们使用了Mapnik的Python接口，搭配定制的OpenStreetmap-Carto风格页，得到了一个高速的栅格化工具，如下图所示。

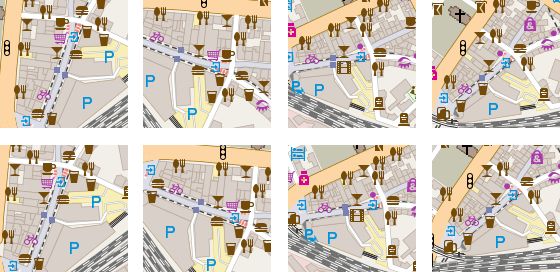
我们的栅格化服务可以通过参数方便地进行数据增强，也就是在生成图块前旋转、平移地图，如下图所示。

这些图块均表示同一位置，但朝向、偏移量不同

从图像到张量

尽管这些栅格化图块让编码器可以很容易地学习捕捉空间结构和关系，却有大量信息在栅格化的过程中丢失了。实际上，栅格化合并了所有多边形和多段线，例如道路、建筑、停车场轮廓、河流，等等。由于GIS数据库包含这些结构的单独信息，让神经网络编码器学习如何分割这些结构毫无道理。

因此，我们并没有将数据栅格化为三通道RGB图像（如上面的示意图所示）。相反，我们修改了栅格化工具，生成一个12通道的张量，每个通道包含不同类型的栅格化信息。

为了便于可视化，本文剩下的部分常常使用RGB栅格化图块，实际上它代表12通道张量。

表示学习

空间相似性

我们的目标是学习一个度量空间，其中语义相似的图块对应相近的嵌入向量。那么，问题在于如何定义“语义相似”？

一个朴素的方法是将每个图块表示为直方图，然后应用k-均值聚类，接着使用词袋模型建模空间。然而，我们不清楚各个通道应该分配多少权重。例如，如果道路相似，但建筑不相似，那么这两个图块仍然算语义相似吗？

此外，即使两个图块有相似的直方图，也不能给我们提供位置周边的空间结构信息。如果图块的一半被大海覆盖，那么这个图块和另一个包含大量小池塘、喷水池的图块在语义上相似吗？下图中的两个图块会产生几乎一模一样的直方图：

然而，这两个图块在语义上并不相同。第一个图块覆盖的是相互连接的道路，第二个图块覆盖的是一些小路，这些小路可能通向人们的住所。事实上，在我们的嵌入空间中，这两个图块对应的嵌入之间的欧几里得距离可不小（||p1-p2||2=2.3），尽管两者的直方图的卡方距离接近零。

除了使用直方图，每个通道也可以总结为一组特征，例如方向梯度的直方图，或者更传统的SIFT或SURF。然而，我们并不打算手工指定哪些特征定义了语义相似性，相反，我们决定借助深度学习的力量，学习自动检测有意义的特征。

为了达成这一点，我们将12通道张量传入作为编码器的卷积神经网络。该网络以自监督的方式基于三重损失函数训练，这意味着无需手工标记的训练数据。

自监督学习：三重网络

Ailon等提出的三重损失这一概念，借鉴自孪生网络架构，可以基于无监督特征学习进行深度度量学习。

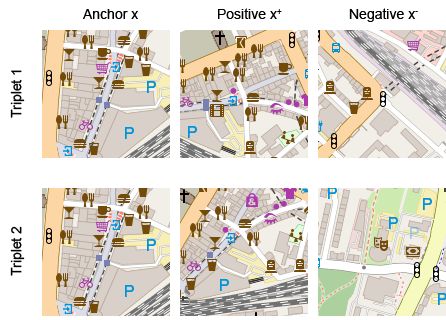
三重网络是一个基于三元组(x, x⁺, x^-)训练的神经网络架构：

• 锚实例x

• 和x语义相似的正例x⁺

• 和x语义相异的反例x^-

接着训练神经网络学习满足下式的嵌入函数f(.)：

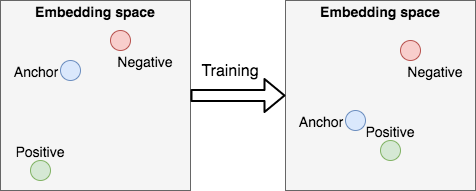
从而直接优化度量空间，如下图所示：

Google的FaceNet让基于三重网络的度量学习变得更流行了，FaceNet使用三重损失学习类似面孔接近、不同面孔疏远的面部图像嵌入空间。

对面部识别而言，正例图像是和锚图像属于同一人的图像，而反例图像是从mini batch中随机选择的人的图像。然而，我们的例子没有这么容易选取正例、反例的分类。

为了定义位置的语义相似性，我们可以利用Tobler的地理第一定律：“所有位置之间都有关系，但近处的关系比远处的关系密切。”

令I(.)为位置坐标到栅格化图块的映射，给定变换T(.)，该变换在生成位置X的栅格化图块前先旋转、平移地图，然后给定一个随机位置Y，满足X ≠ Y，那么我们便得到了三元组：

• x = I(X)

• x⁺ = I(T(X))

• x^- = I(Y)

因此，我们假定地理上相邻、部分重叠的两个图块，相比完全不同的两个图块，在语义上更相近。

为了避免网络仅仅学习琐碎变换，我们在训练过程中随机开启或关闭正例图像12个通道中的部分通道，迫使网络在信息的随机子集不同（例如，没有建筑物，没有道路，等等）的情况下，学习正例图块的相似性。

SoftPN三重损失函数

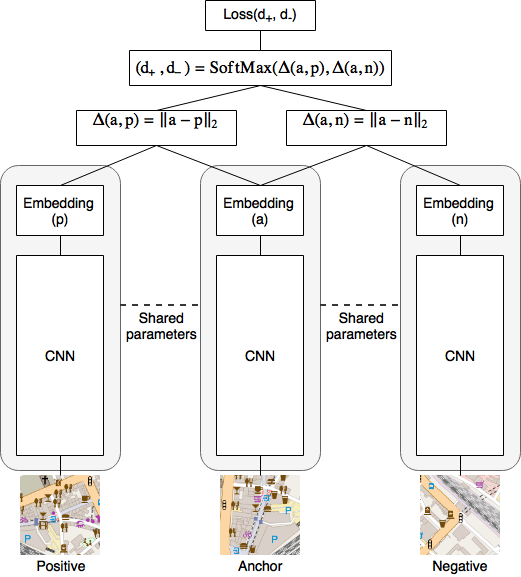
下为我们使用的三重网络的一般结构。

上图中的损失函数的具体定义如下：

所以优化网络等价于最小化向量(d₊, d_-)和向量(0, 1)的MSE。

下面我们解释下为什么损失函数这么定义。我们想要Δ(a,p)尽可能地接近零，Δ(a,n)尽可能大。为了优化这一比率，我们应用softmax，使两者位于[0, 1]之间：

三重损失函数的这一定义经常称为softmax比率，最早由Ailon等提出。

这一定义的主要问题在于，网络会很快学到一个d-接近一的嵌入空间，因为大多数随机负例图像和瞄图像大不一样。因此，大多数(a,n)对优化过程中的梯度没有贡献，导致网络很快停止学习。

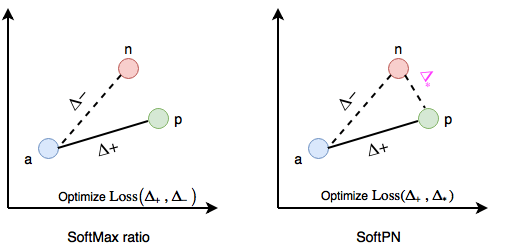
我们可以使用不同的方法解决这一问题，其中之一是难分样本挖掘，精心选择(a,n)以确保网络可以维持学习。然而，在我们的例子中，在不引入偏差的情况下，并不总是清楚如何有效地选取难分样本。而Balntas等提出的SoftPN三重损失函数，是一个更简单的方案。

SoftPN损失将上述softmax计算中的Δ(a,n)替换为min(Δ(a,n), Δ(p,n))。这就使网络在优化过程中，试图学习一个锚嵌入和正例嵌入都尽可能远离反例嵌入的度量空间。相反，原本的softmax比率损失只考虑锚嵌入和反例嵌入的距离。

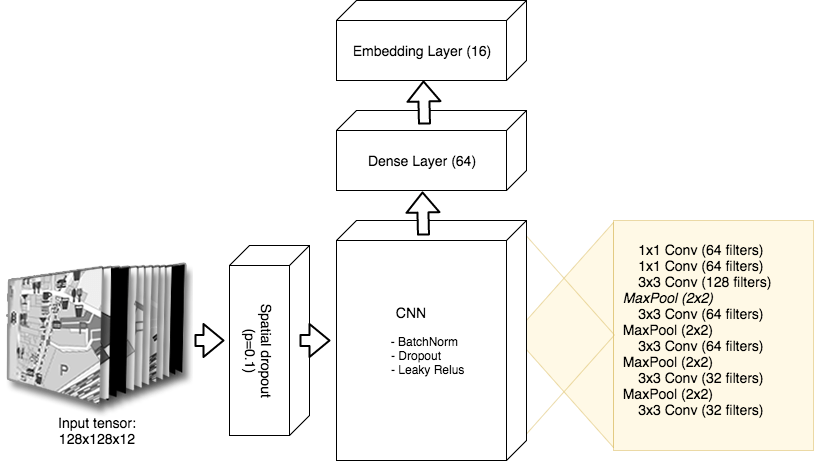
神经网络架构

编码器部分我们用了相当传统的卷积神经网络架构，包含5个卷积层，过滤器大小为3x3，接着是两个一维卷积层，一个密集层。一维卷积通过跨通道参数池化起到降维作用。

嵌入层由另一个密集层加上一个线性激活函数构成，线性激活函数使得输出范围不限于前一层非线性激活的正值区域。完整的网络架构如下图所示：

我们激进地使用dropout和BN，同时使用了Leaky ReLU激活函数，因为我们在刚开始的测试中碰到了死亡ReLU问题。

此外，我们直接对输入应用了空间池化，完全丢弃一个随机选择的通道，迫使网络通过关注不同的通道学习区分图像。

整个网络基于Keras实现，仅包含305040参数，使用Adam优化在p3.2x large AWS主机上训练了两周。

训练数据

我们获取了用户在我们平台上访问的约一百万位置，并增加了用户沿途拍摄的接近五十万位置。

我们将这一百五十万位置中的每个位置栅格化为128×128×12的图块，表示该位置方圆一百米内的区域。这些张量用作锚图像。

我们同时为每个位置栅格化20张随机平移、旋转的图块，用作正例图像。横纵两方向的偏移均匀取样自0到80米的区间。最终，每个位置得到了20对(锚，正例)，共计三百万张图像。

网络训练生成mini batch时同时生成三元组。每个mini batch包含20个位置。每个位置随机选择5对(锚, 正例)，而反例图像则随机取样自mini batch，这样每个mini batch大小总共为100。

在生成mini batch的同时生成三元组，实际上我们得到了一个几乎无限大的包含独特的三元组的数据集，鼓励网络在许多epoch后持续学习。

可视化过滤器和激活函数

由于嵌入空间是以自监督的方式学习的，没有使用标注数据，所以难以监测网络是否真的在训练中学到了东西。

可视化网络学习到的过滤器是一个不全面但仍然很有用的检查方法。事实上，我们想要可视化可以最大化网络不同层的激活的输入图像。

为了做到这一点，我们可以从一个随机生成的图像开始，将每个像素看成需要优化的一个参数。接着我们使用最大化选定层输出的梯度上升更新图像的参数。

计算输入图像在卷积层输出激活的均值上的梯度，基于若干次迭代进行的梯度上升，能够生成高亮网络层最关注的结构的图像。

因为我们的输入是一个12通道张量，而不是RGB图像，所以我们直接从12个通道中选择了像素值均值最大的3个通道，将其转为RGB图像。我们在每个通道上应用了直方图均衡化，以进一步增强视觉细节。

下图显示了位于底部的一个网络层的每个32过滤器。显然，这一层看起来更关注底层细节（道路、小块结构等）。

对比位于上部的一个网络层的64过滤器，很明显，这些过滤器更容易被更平滑、更复杂的结构激活。这一对比也许意味着整个网络能够学习输入的层级特征分解。

高层倾向于通过组合低层学习到的低层特征学习更复杂的结构

尽管我们不应该过高估计这些可视化的有用程度，但它们确实看起来很有意思，特别是在多次研究迭代之间。例如，早期版本的可视化快速地指引了正确方向，发现了我们网络中的一堆死亡ReLU。我们后来通过替换激活函数为Leaky ReLU解决了这一问题。

探索度量空间

可视化嵌入

可视化网络学习到的过滤器主要用于调试，但在判断学习到的嵌入空间的质量方面没有多大帮助。

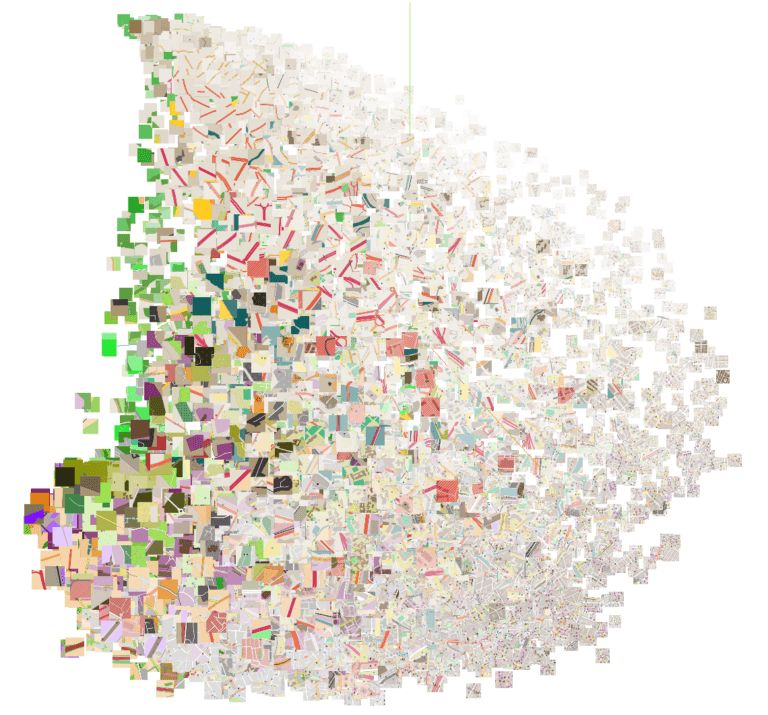
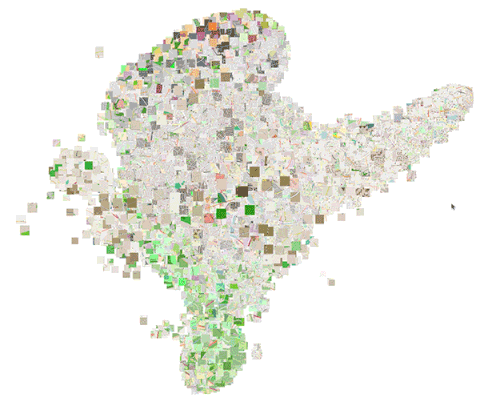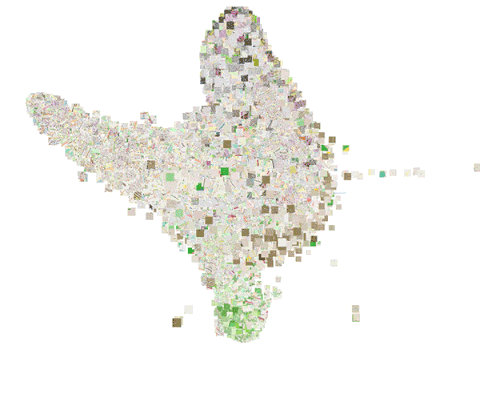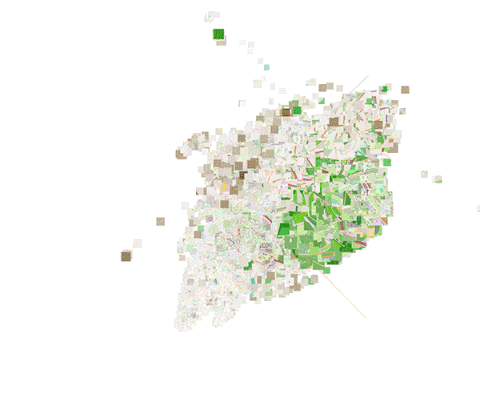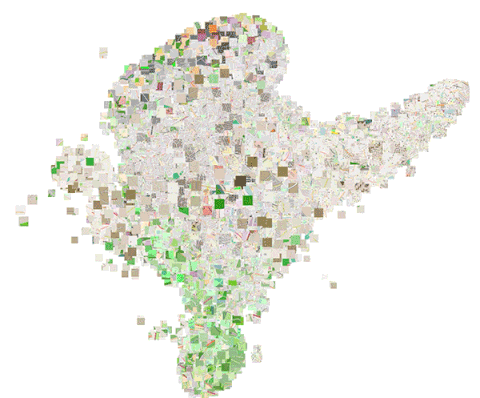
为了大致了解嵌入空间看起来什么样，我们使用PCA将维度降至三维后，可视化了嵌入空间。为便于解释，每个位置嵌入可视化为相应的栅格化图块。

显然，即便只留下三个主成分，这三个分量仍然捕捉了大量有意思的信息。公园等绿化区域、道路区域、（右下角的）城市中心区域区别非常明显。

下图是一个嵌入空间的三维t-SNE动画，更清楚地显示了这些局部结构的差异。

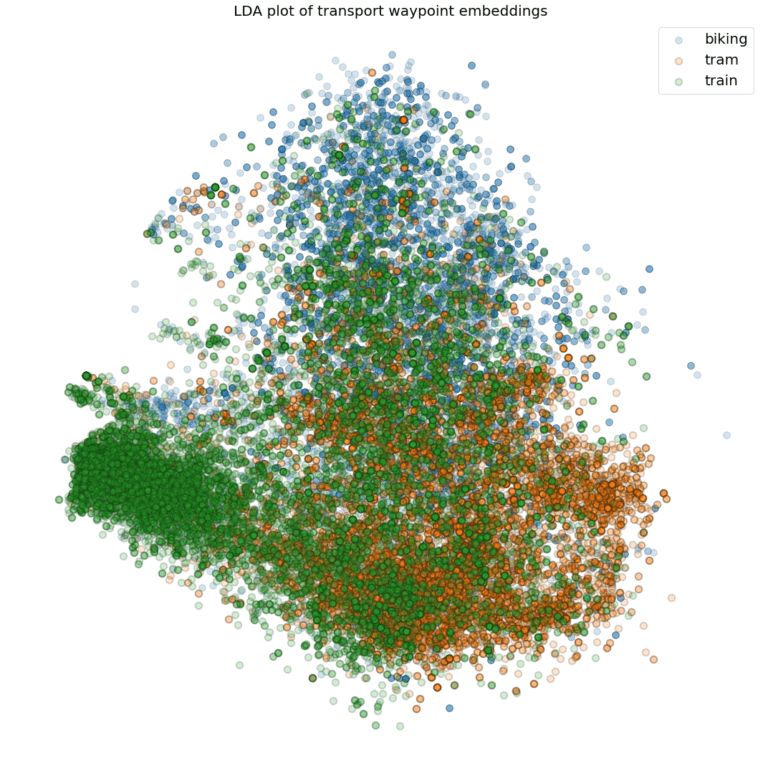
这些嵌入不仅可以用于地点映射，还可以用在我们的交通路线分类器中。下图显示了取自我们的交通路线分类训练集的位置嵌入的散点图。这里，我们使用线性判别分析（LDA）将16维嵌入空间映射至二维。

上图显示，不同的交通方式一般发生在不同的区域。例如，我们的嵌入捕捉了关于铁轨和电车站的信息。

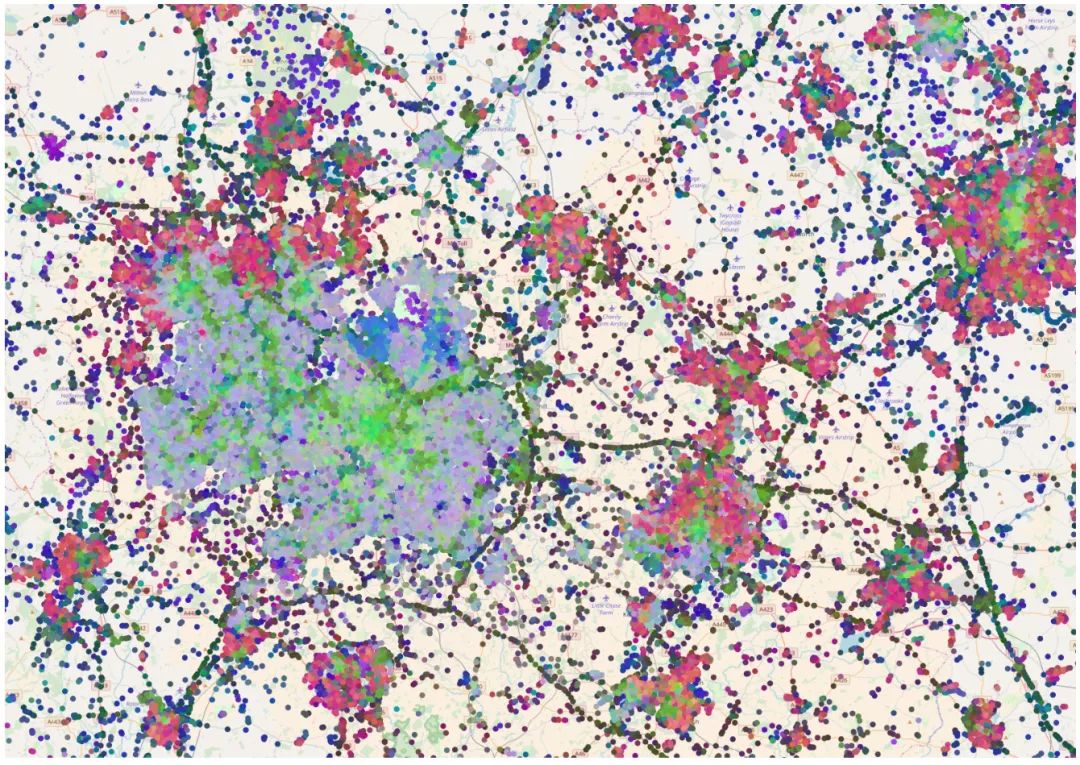
为了显示不同的地理区域是如何编码的，我们使用PCA将16维嵌入降至三维，缩放后直接作为RGB颜色值使用，以便在地图上绘制测试数据集。下图可视化了伦敦区域，清楚地体现了市中心、公路、水域、旅游区域、住宅区的编码各不相同。

通过可视化伯明翰区域，可以揭示，与充斥大量建筑的伦敦相比，伯明翰有一个更大的郊区。

空间内的随机行走

我们可以通过随机行走进一步检验嵌入空间的平滑性。随机行走从一个随机的种子点开始，每次跳跃随机选择当前嵌入的k近邻中的一个，然后可视化相应的图块。

下图显示了6次随机行走的结果。注意，大多数情况下，嵌入空间的最近邻在地理上相距数百千米、数千千米，但在语义上高度相似。

位置计算

尽管上面的可视化表明学习到的嵌入空间是平滑的，也捕捉到了语义相似性，但并不能证明我们确实学到了一个欧几里得度量空间——我们可以在嵌入之间插值，在嵌入上进行基本的算术运算，并得到有意义的结果。

下图演示了在两个嵌入（最左、最右）之间插值的结果。插值的每一步所得，映射至测试数据中的最近嵌入，然后可视化相应的图块。

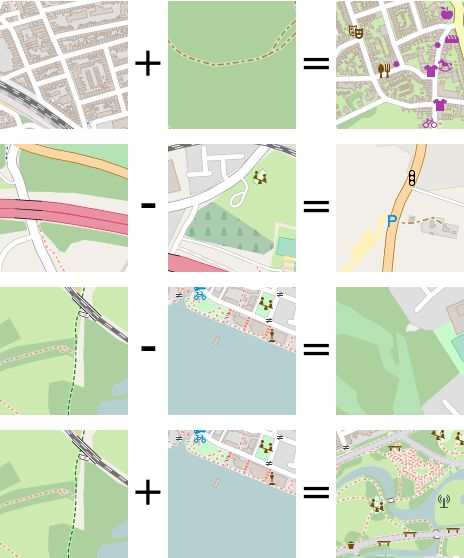
最后，下图显示了加上嵌入或减去嵌入，并将结果映射至测试数据中的最近邻，会发生什么。

这些结果表明，我们的嵌入空间确实表示了一个距离具有意义、基本算术规则成立的度量空间。

由于度量空间是基于自监督方式训练得到的，我们可以使用大量未标签数据迫使网络学习捕捉有意义的关系。因此，在后续分类器中使用这些嵌入作为特征向量，是一种迁移学习的形式，让我们可以基于非常有限的标注数据训练强大的分类器。

结语

本文显示了如何使用三重网络学习捕捉不同地理位置坐标间的语义相似性的度量空间。

我们训练卷积神经网络学习提取定义语义相似性的特征，然后通过度量学习得到一个嵌入空间。

所得嵌入空间可以直接用在地点映射或交通路线分类这样的任务上，通过迁移学习帮助我们大大改善分类器的精确度和概括能力。

此外，这些嵌入给分类器带来了某种直觉，使得错误的分类仍然可以作出直观的解释。例如，我们的地点映射器很快学习到将日间活动和夜间活动绑定到不同的特定区域，例如工业区、市中心、公园、火车站等。

如果你想了解更多关于我们平台的信息，或亲自试用，欢迎联系info@sentiance.com，或下载我们的演示应用Journeys：http://www.sentiance.com/demo

参考

1. 词嵌入：https://arxiv.org/abs/1301.3781

2. 基于三重网络的深度度量学习：https://arxiv.org/abs/1412.6622

3. Facenet: https://arxiv.org/abs/1503.03832

4. PN-Net: https://arxiv.org/abs/1601.05030

5. 网中网：https://arxiv.org/abs/1312.4400

原文地址：https://www.sentiance.com/2018/05/03/loc2vec-learning-location-embeddings-w-triplet-loss-networks/