论文浅尝 | 重新实验评估知识图谱补全方法

论文作者：Farahnaz Akrami，美国德州大学阿灵顿分校，博士生。

笔记整理：南京大学，张清恒，硕士生。

---

     

链接：https://arxiv.org/pdf/2003.08001.pdf

代码：https://github.com/idirlab/kgcompletion

一、概述

目前的知识图谱（KG）规模庞大，但还远远不够完备。近年来，知识图谱补全（KGC）研究已然成为热门话题，其目标是将缺失的事实补充到KG中。研究者们对KG表示学习模型或嵌入（embedding）模型进行了广泛的研究，提出了众多新的嵌入模型。我们进行了实验研究以评估这些方法，本文将发表在SIGMOD 2020。

本文主要研究了KGC方法的真实有效性，同时发现了基准数据集FB15k、WN18以及YAGO3-10中存在的缺陷。这些数据集被广泛用于训练和评估众多嵌入模型，它们包含大量的反向和重复三元组，本文揭示了这些数据集中存在的数据冗余和测试集遗漏问题对嵌入模型的影响。本文研究的另一问题是FB15k数据集中存在笛卡尔积关系。数据集中存在的上述问题会导致模型准确性出现误差。此外，使用这些数据集训练KGC模型容易导致过拟合，使用上述三元组优化的模型，很难被推广到真实的应用场景中。简而言之，通过研究有以下发现：

1. 广泛使用的基准数据集中存在数据冗余和测试集遗漏等问题，导致许多模型的准确性被高估了19％-175％；

2. 我们发现笛卡尔积关系也会导致性能评估出现误差；

3. 用于评估模型的许多测试用例在现实场景中不是真实存在的。

二、嵌入模型与相关数据集

对于KG中的三元组(head entity, relation, tail entity)，使用 (h, r, t) 表示，嵌入模型学习它们的多维表示 h，r，t。众所周知，数据集在训练机器学习模型中起着重要作用。用于训练和测试嵌入模型的数据集存在各种问题，因此这些模型在真实场景下难以发挥效果。

FB15k & FB15k-237

FB15k数据集中包含很多反向关系，存在大量的反向三元组(h,r,t)和(h,r^{-1}, t)，其中 r 和 r^{-1} 是反向关系。例如，(Avatar, film/directed_by, James Cameron)和(James Cameron, director/film, Avatar)是一对反向三元组。事实上，Freebase 使用一种特殊的关系reverse_property 来表示反向关系，例如，(film/directed_by, reverse_property, director/film)。在FB15k中，训练集中大约有70%的三元组存在反向关系，在测试集中大约有70%的三元组，其对应的反向三元组存在于训练集中。

这些数据特征表明，在链接预测任务中，嵌入模型将偏向于学习反向关系。更具体地说，该任务在很大程度上可以推断出两个关系r1和r2是否形成反向对。考虑到数据集中存在大量的反向三元组，可以不使用复杂的实体和关系嵌入模型实现上述目标。可以使用数据集中三元组的统计信息来生成类似(h,r1,t) => (h, r2, t)形式的简单规则。实际上，本文使用这样一个简单的模型，在FB15k上 FHits@1↑ 指标达到了71.6%，作为对比，目前性能最优的模型在FB15k上FHits@1↑ 的结果为73.8%。

值得注意的是，如果给定这类数据，链接预测任务在真实世界中是不存在的。对于FB15k而言，来自Freebase的冗余反向关系是人为创建的。新的事实总是作为一对反向三元组添加到Freebase中，由关系reverse_property明确表示。对于这种总是成对出现的内在逆向关系，当某个三元组对应的反向三元组已经出现在KG中时，我们是不需要预测该三元组的。因此，使用FB15k训练KGC模型会出现过拟合问题，因为学习的模型针对反向三元组进行了优化，而反向三元组无法推广到实际应用中。

文章[1]注意到了FB15k存在的上述问题，并通过去除反向关系构造了新的数据集FB15k-237。为了进一步研究FB15k中冗余数据的影响，我们进行了一些实验，比较了FB15k与FB15k-237上的几种嵌入模型的结果，下表显示了这些模型在不同指标上的结果。

             

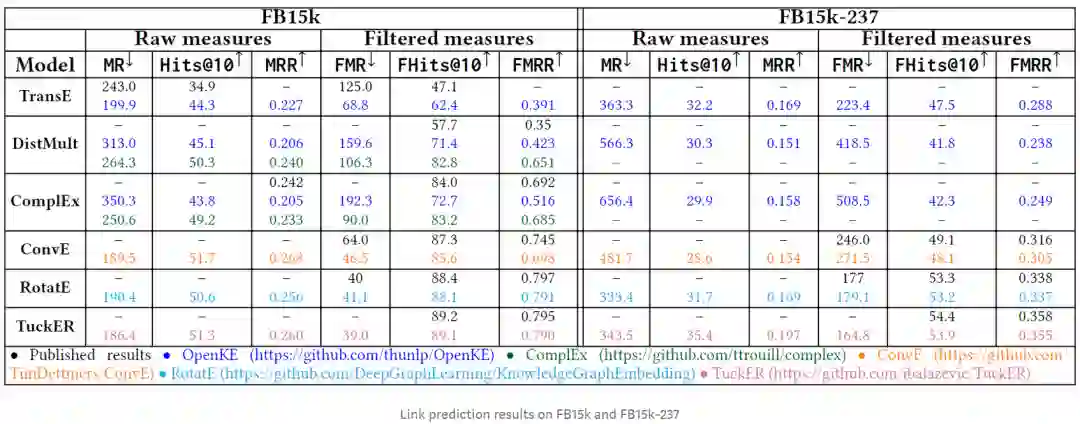
通过实验得出的总体观察结果如下：

1. 删除反向关系后，所有方法的性能都会大大降低。正如下面的雷达图所示，在FB15k-237上嵌入模型的性能大大降低。该结果验证了基于嵌入的方法只能在反向关系上表现良好，然而，基于反向关系推理的直接方法可以实现相当甚至更高的精度。

             

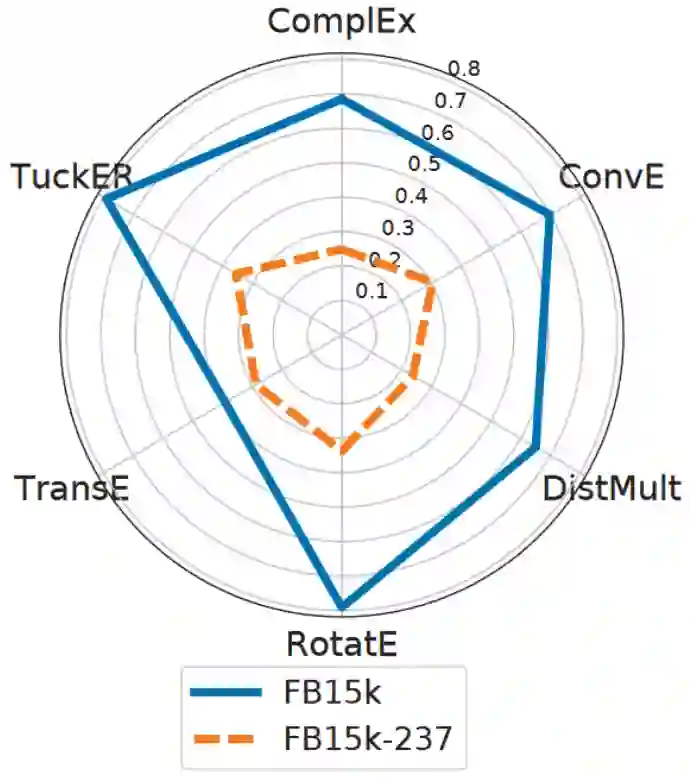
2. 先前的很多工作认为一些基于TransE的改进方法明显优于TransE，我们在FB15k上的实验也证实了这一点，但在FB15k-237上它们的差距并不大。我们认为这些模型主要在反向和重复三元组上提升了结果，因此在删除这些三元组后，它们没有表现出明显的优势。这个假设可以通过我们的发现得到验证，这些模型能够正确预测而TransE未能正确预测的大多数三元组，在训练集中都有反向或重复的三元组。

WN18 & WN18-RR

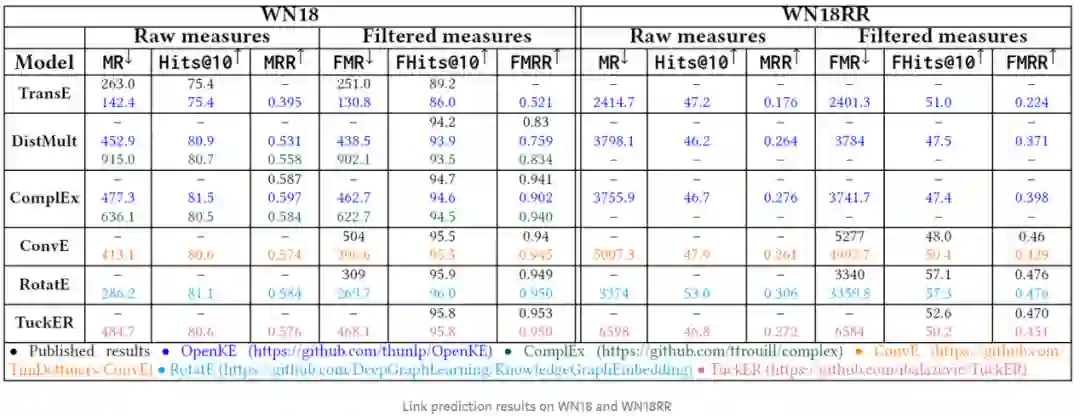
WN18也存在反向关系的问题，WN18中共有18种关系，其中14种关系构成了7对反向关系对，例如(europe, has_part, republic_of_estonia)和(republic_of_estonia, part_of, europe)是反向三元组，它们涉及到的反向关系是has_part和part_of。与此同时，WN18中还有三种自反关系，分别是verb_group、similar_to和derivationally_related_form。训练集中约有93％的关系三元组，而测试集中有93％的三元组，在训练集种存在反向三元组。

为了消除WN18反向关系，文章[2]通过保留每对反向关系中的一个关系，构造了新的数据集WN18-RR。我们比较了在WN18和WN18-RR上嵌入模型的结果，得出的结论与在FB15k和FB15k-237上观察到的结论相同。具体结果如下表所示。

            

YAGO3-10 & YAGO3-10-DR

YAGO3-10具有37种关系，其中isAffiliatedTo (r1)和playsFor (r2)这两个关系所涉及到的三元组，在训练集种分别占35％和30％。在现实世界的语义上，r1包含r2，但由于它们的(subject, object)对基本上重叠，因此它们在此数据集中以重复关系出现。根据我们的实验，各种模型在r1和r2上取得的结果比其他关系要强得多。通过删除YAGO3-10中的冗余数据，本文构造了一个新的数据集YAGO3-10-DR。通过对比YAGO3-10和YAGO3-10-DR，我们得出的结论与在其他数据集上观察到的结论相同。

三、笛卡尔积关系

本文还在FB15k上发现了另一个问题，本文称为笛卡尔积关系（Cartesian product relations）问题，这个问题会导致嵌入模型的现有性能指标与实际不符。对于一个笛卡尔关系，其所涉及到的三元组中的subject-object对构成了对应的笛卡尔积。例如，关系climate是一个笛卡尔积关系，因为(a, climate, b)对于每个可能的城市a和月份b，都是有效的三元组。再例如，关系position也是一个笛卡尔积关系，因为在确定的职业体育联盟中的每个队伍都有相同的位置。对于这样的关系，链接预测问题就变成了预测一个城市是否有其一月份的气候，或者某支NFL球队是否有四分卫位置。这些关系的存在变相提高了模型的精度，而且这样的预测任务意义不大。与我们观察到的反向关系相同，FB15k中笛卡尔积关系也是人为构建的。实际上，60％的笛卡尔积关系是由特殊的“中介节点”造成的。如果要对笛卡尔积关系进行链接预测，一种简单的方法比学习复杂的嵌入模型更有效。我们实现了一种简单的方法来查找笛卡尔积关系，并在这些关系上进行链接预测任务。我们在FB15k中的9个笛卡尔积关系上进行了实验，使用简单方法获得的平均FHits@10↑ 为98.3％，高于TransE的效果（96.3％）。

 

参考文献

[1]Toutanova, Kristina , and D. Chen. "Observed Versus Latent Features for Knowledge Base and Text Inference." Workshop on Continuous Vector Space Models & Their Compositionality 2015.

[2]Tim, Dettmers, and Pasquale, Minervini, and Pontus, Stenetorp, and Sebastian, Riedel. "Convolutional 2D Knowledge Graph Embeddings." AAAI 2018.

---

 

OpenKG

开放知识图谱（简称 OpenKG）旨在促进中文知识图谱数据的开放与互联，促进知识图谱和语义技术的普及和广泛应用。

点击阅读原文，进入 OpenKG 博客。