OpenAI发布可扩展的元学习算法Reptile | 论文+代码+Demo
安妮 编译自 OpenAI官方博客
量子位 出品 | 公众号 QbitAI
昨天,OpenAI发布了一种新型的可扩展元学习算法Reptile,还能在线试玩。
何为Reptile?难道是——
咳咳严肃一点。
据OpenAI官方博客显示,这是通过重复对一个任务进行采样、随机梯度下降并将初始参数更新为从任务中学习到的最终参数的算法。
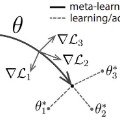
这种方法不禁让人想到去年七月伯克利AI研究所关于未知模型元学习法(MAML)的研究。OpenAI表示,Reptile的效果和MAML相似,但实现起来更简单,计算效率更高。
UC伯克利MAML相关论文:
http://bair.berkeley.edu/blog/2017/07/18/learning-to-learn/
试玩demo
元学习(Meta-learning)是一种学习如何学习的过程。向元学习算法中输入任务的分布,相当于每个任务都是一个需要学习的任务,算法会产生一个快速的learner,每个learner可以从少数样例中进行归纳。
小样本学习(Few-shot Learning)分类问题是元学习中研究得比较充分的课题,learner只能从每个类中看到1-5个输入-输出样例,然后对新的输入进行分类。
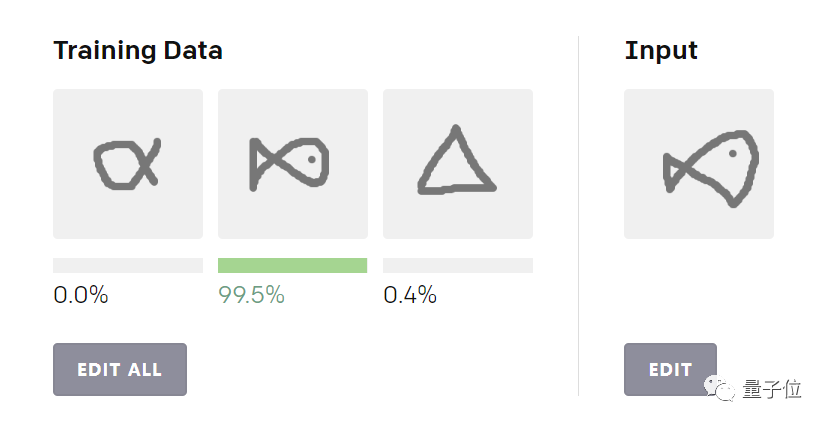
下面是一个one-shot交互式演示的demo,可以在OpenAI的博客上试玩这个应用了Reptile小模型。
△ 前三张图为标记样例,每张代表一个类别;最右是输入未知样例,Reptile将它划分到最像的类别中
你可以通过点击“Edit All”(编辑所有),随心画三个不同的形状,然后在最右边的输入栏中再画一个,看看Retile是如何对它进行分类的。
量子位也随手画了几笔参与了一下这个项目:
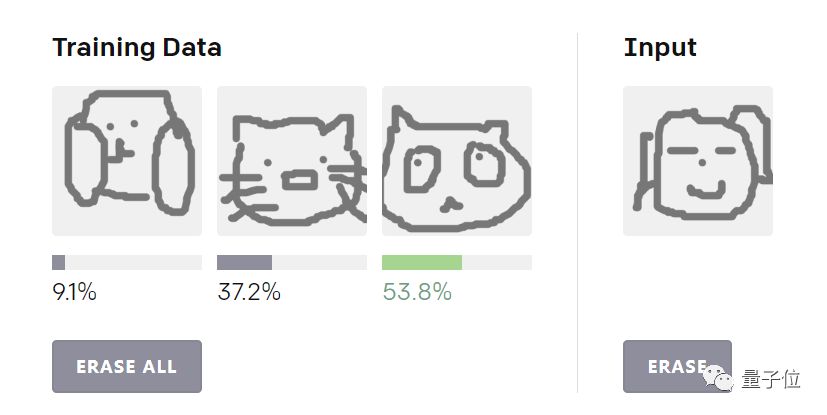
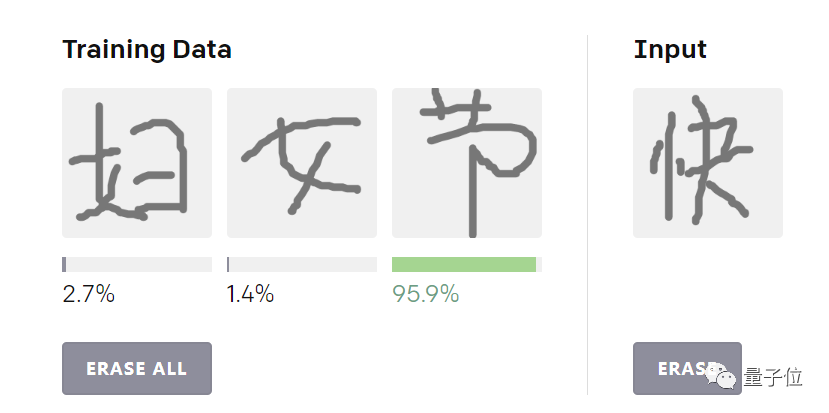
Reptile认为,量子位手画的小女孩应该属于“熊猫”分类,手写的“快”字和“节”更相像,应该分到这个分类中的可信度高达95.9%。
想试玩demo可以移步介绍页面:
https://blog.openai.com/reptile/
目前,相关研究的论文也已经放出:
https://d4mucfpksywv.cloudfront.net/research-covers/reptile/reptile_update.pdf
So does 代码(TensorFlow实现):
https://github.com/openai/supervised-reptile
一个基于JavaScript的实现(文中我们玩的那个demo就是用它做的~):
https://github.com/openai/supervised-reptile/tree/master/web
祝你玩得开心~
— 完 —
加入社群
量子位AI社群15群开始招募啦,欢迎对AI感兴趣的同学,加小助手微信qbitbot6入群;
此外,量子位专业细分群(自动驾驶、CV、NLP、机器学习等)正在招募,面向正在从事相关领域的工程师及研究人员。
进群请加小助手微信号qbitbot6,并务必备注相应群的关键词~通过审核后我们将邀请进群。(专业群审核较严,敬请谅解)
诚挚招聘
量子位正在招募编辑/记者,工作地点在北京中关村。期待有才气、有热情的同学加入我们!相关细节,请在量子位公众号(QbitAI)对话界面,回复“招聘”两个字。
量子位 QbitAI · 头条号签约作者
վ'ᴗ' ի 追踪AI技术和产品新动态