ICCV2019 Oral | 用于人群计数的贝叶斯损失函数

    点击上方“CVer”，选择加"星标"或“置顶”

重磅干货，第一时间送达

作者：Zee Jay

https://zhuanlan.zhihu.com/p/91834072

本文已授权转载，未经允许，不得二次转载

1.Contribution

本文全程把counting当作是一个概率问题，预测的density map是一个概率图，每个点表示该点处有人存在的概率，把density map每个点看作是样本观测值，然后这个点存在某个人的概率当作先验概率，用均匀分布表示，即每个点可能存在N个人中的某一个，或者是背景，然后基于观测值和先验概率，我们可以估计该点处是否存在某个人的后验概率，后验概率其实是对真实分布的估计，ground truth就是真实分布，因此拿后验概率与真实概率做差，就可以作为loss去优化模型

2.Method

（1）关于贝叶斯估计的背景知识

贝叶斯估计是参数估计的一种，所谓参数估计，就是实现假定数据服从某个分布，比如高斯分布，那么我们就希望通过实际的数据去确定高斯分布N(μ，σ）的均值μ和方差σ，这两个一旦确定，我们就相当于获得了数据的预测模型，大致上对未来获得的新的数据心里有了大概的一个估计，

参数估计最常用的有极大似然估计和贝叶斯估计，极大似然估计的基本思想是，当取得一组观测数据之后，μ和σ取什么值，最可能会得到这组观测数据，就像医生看病一样，他通过询问你问题，获得有关病情的观测数据，然后他就在推断，哪种病最可能会导致病人的这种状况，极大似然估计就是在做这个推断，具体的方法是要将概率密度函数乘起来，代入观测值，并求导，找到极值的过程，这里不展开，但是你得知道，极大似然估计它估计了一个具体的μ和σ的值

贝叶斯估计不像极大似然估计那么绝对，就认为μ和σ就是算出来的两个值，贝叶斯估计它通过观测值去估计μ和σ可能服从的分布，也就是说，贝叶斯估计，估计的是参数本身服从的分布，相比于极大似然估计的精确估计，贝叶斯估计则是一种模糊的估计，具体如下：

事先，你也要假设一下参数服从的分布，如果有事先的经验，那就可以根据经验设计一个参数服从的分布，如果事先啥都不知道，那么就先假设维正态分布，因此我们称这个事先假设的参数分布为先验分布，

即常用p(θ)=π（θ），π表示某种先验分布

当然先验分布只是事先假设，不一定对，我们要通过观察数据样本，根据观察值，来对先验分布进行修正，用D表示一组观测值，如下所示：

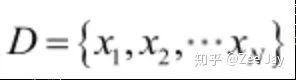
基于这组观测值，我们可以利用贝叶斯定理，反推这样一组观测值是θ取某个值所导致的概率的大小，以下就是贝叶斯定理的公式了：

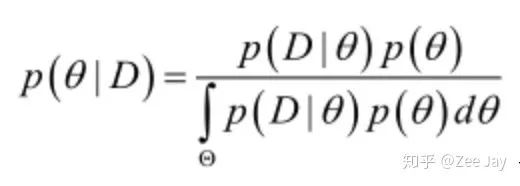
这个通过贝叶斯公式推断的各种θ的可能性，就是θ所服从的后验分布，也就是根据观测值修正后的分布，所以其实贝叶斯公式只是一个公式，贝叶斯估计是拿贝叶斯公式进行参数估计的一种估计方法

其实到这里已经用完了贝叶斯估计了，接下来你若一定要得到参数θ的一个估计值，那往往用后验概率的期望值去作为参数θ的估计值：

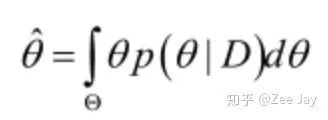
上面这个就是连续随机变量的期望计算公式

（2）看看本文怎么把贝叶斯估计跟counting结合的

首先本文从某个人出现在某个位置的概率问题用贝叶斯估计去代入，如下所示：

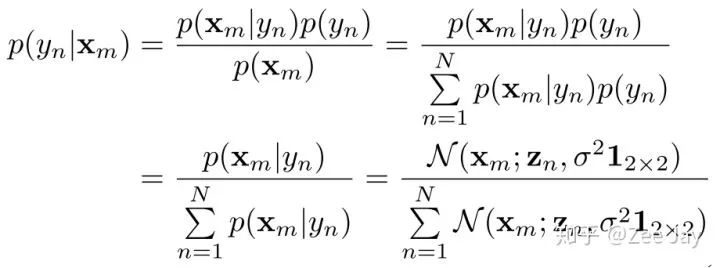
Xm表示density map上某个位置，yn表示第n个人，总共是N个人，观测值是Xm，表示Xm处观测到一个人，然后p(yn|Xm)在Xm处观测到的人是yn的概率，Xm处观测到的人可能是N个人中的任意一个，所以先验分布p(yn)用均匀分布1/N表示，然后p(Xm|yn)表示yn出现在Xm处的概率，那么这个概率好表示，文中用了2D的高斯分布表示：

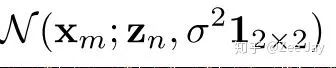
等于:

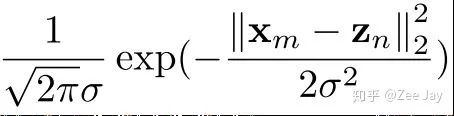
Zn表示yn这个人所在的坐标，也就是说距离yn越远，那yn出现在这里的概率就越小。

以上p(yn|Xm)就是Xm处要是存在一个人，那么这个人是yn的概率，然后利用期望，本文求了yn这个人出现在整张图上的概率

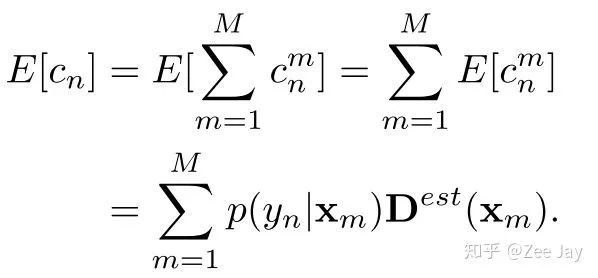
预测的density map有M个点，然后每个点的值代表该点处存在一个人的概率，然后结合后验概率p(yn|Xm)的概念，上面的公式表示yn这个人在整张density map上出现的概率，当然他是存在的，且应该是1，所以ground truth就是1，所以loss可以表示为如下所示：

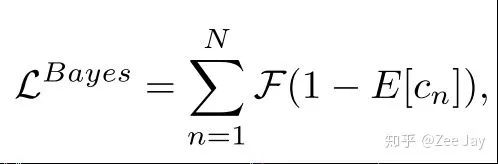
这就是本文的核心，即贝叶斯loss，F在这里表示L1的loss，即绝对误差。因此本文是在根据预测的density map，来推断每个标注了的人存在的概率，期望每个标注了的人存在的概率接近于1。

（3）测试的时候怎么做

以上贝叶斯loss的推断过程解释了本文如何训练模型，但是测试的时候，我们就是输入图片，输出一张density map，然后如何表示预测的人数呢？还像以前一样对density map求和就表示人数了吗？答案是yes！按照概率的思想，根据预测的density map，我们用期望的方式去分析每个标注了的人存在的概率，然后加起来，就是总人数，按照这个逻辑，我们得到了下面的公式：

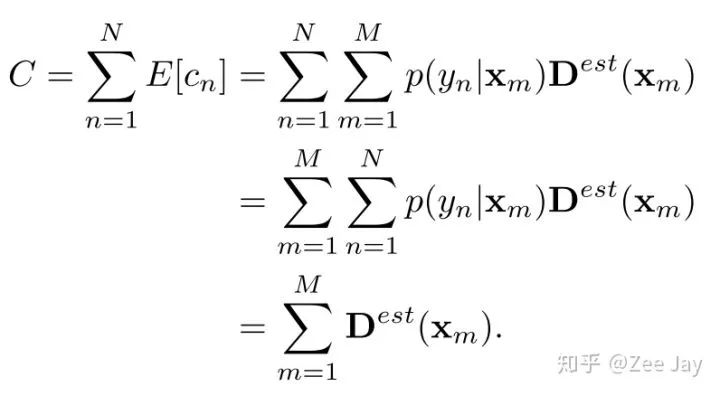
但是对于测试图片，我们不知道标注的人在哪里，因为没有标注，即图中的p(yn|Xm)不知道，但是把两个求和Σ的顺序对调，先对p(yn|Xm)求和，那因为这个求和就是1，所以剩下来的就是对整张density map求和，所以测试时，还是这么做

（4）考虑背景的影响

以上的贝叶斯loss只考虑了每个人我希望其存在的概率接近于1，但是没有对背景进行约束，即原图中还存在大量背景呢，本文的做法是，在贝叶斯公式中，不仅考虑N个人，还加上了一个背景的选项，即当作现在又N+1人，多的一个人是背景，用y0表示：

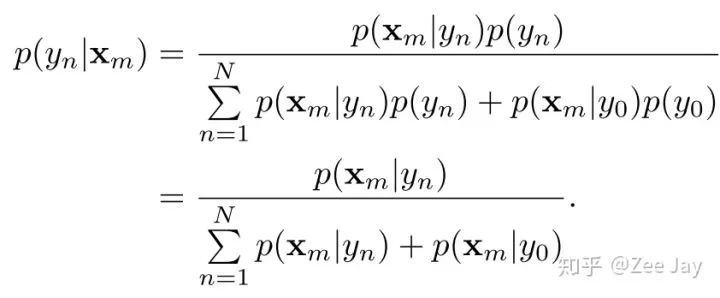
所以后验概率的分母多了背景存在于Xm处的概率，p(Xm|y0), 然后统一p(Xm|yn)和p(Xm|y0)都为1/(N+1)，即把背景也当作一个人，那么后验概率如下所示：

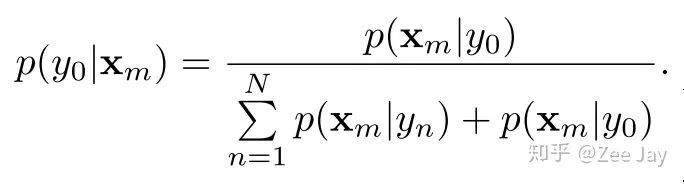
同样，类似于之前根据density map去估计第n个人yn存在的概率，我们也去估计背景人y0存在的概率，用期望计算：

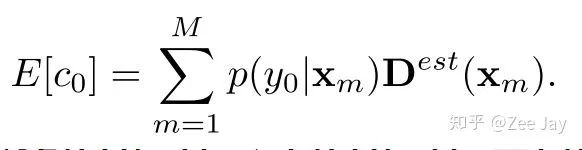
当然由于估计的density map上的每个点表示这里有人的概率，所以一旦Xm处有人，那么Xm处为背景的概率p(y0|Xm)为0，因此上面的期望E[c0]=0. 考虑了背景之后的贝叶斯loss如下所示：

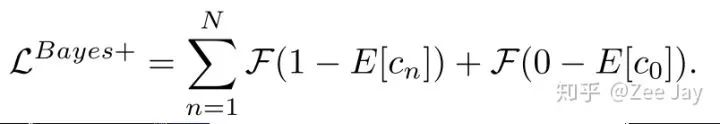
然后背景出现在Xm处的概率，也用2D高斯分布表示，对于某个人yn，这个好办，距离yn越远，则yn出现在这里的概率越小，但是对于背景y0，背景没有一个标注点，那么本文是通过距离最近的标注点越远，就越可能是背景的思想，对y0出现在Xm处的概率建模的，同时提出了一个背景的中心点Z0，如下所示：

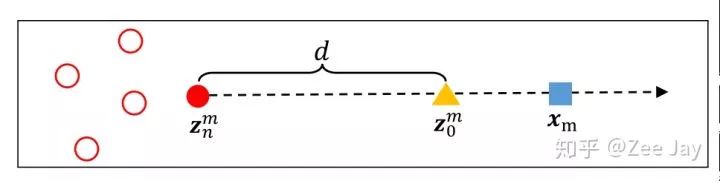
对于Xm这个位置，先找到距离它最近的人头点Zn，然后认为距离Zn的距离为d的点Z0就是一个背景中心点，然后围绕这个假想的背景中心点，用一个2D的高斯分布去建模：

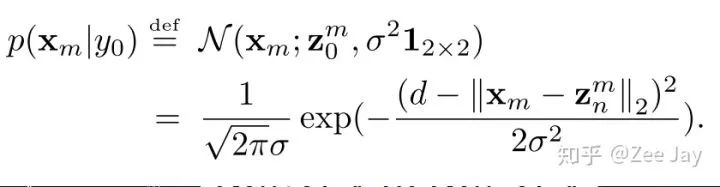
ok，所有的理论推导完了

3.Experiment

（1）本文采用的模型

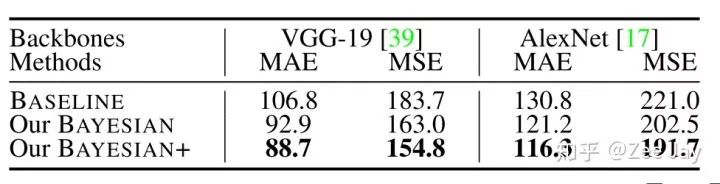
本文采用VGG16和AlexNet作为backbone，对于VGG19，最后输出1/16尺寸太小，于是他们加了一个上采样，到1/8，再预测density map

（2）可视化后验概率分布

每个人在每个位置，都存在一个后验概率分布p(yn|Xm)，然后将N个人的后验概率分布加起来，就得到了整图的后验概率分布了，本文将这个通过计算entropy的方式可视化，

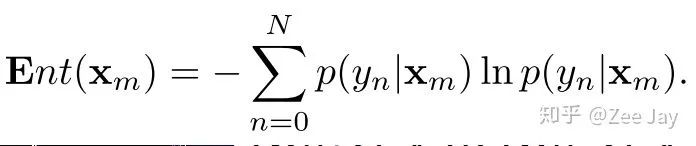
entropy越小，则表示这里要么是人，要么是背景，很明确，如果entropy越大，则表示这里有些模棱两可，

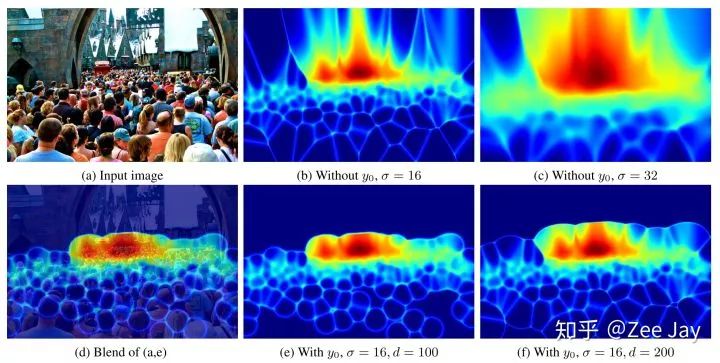
这里越亮越表示模棱两可，越暗表示越明确是人或是背景，然后图中可以看到基本上人头区域都是暗的，人头边界和部分背景比较亮，符合后验概率的计算原理，σ越小图越清晰，因为小的σ不容易导致两个人头区域有重叠，d越小，则表示某个点更容易倍判断为背景，图中的e比f人头轮廓更合理，是因为被判断为背景的点更多

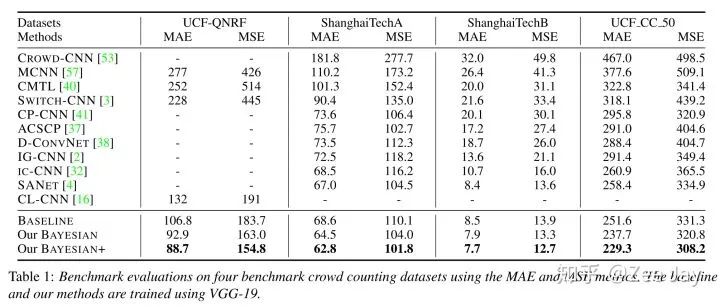
（3）与SOTA的比较

（4）ablation study

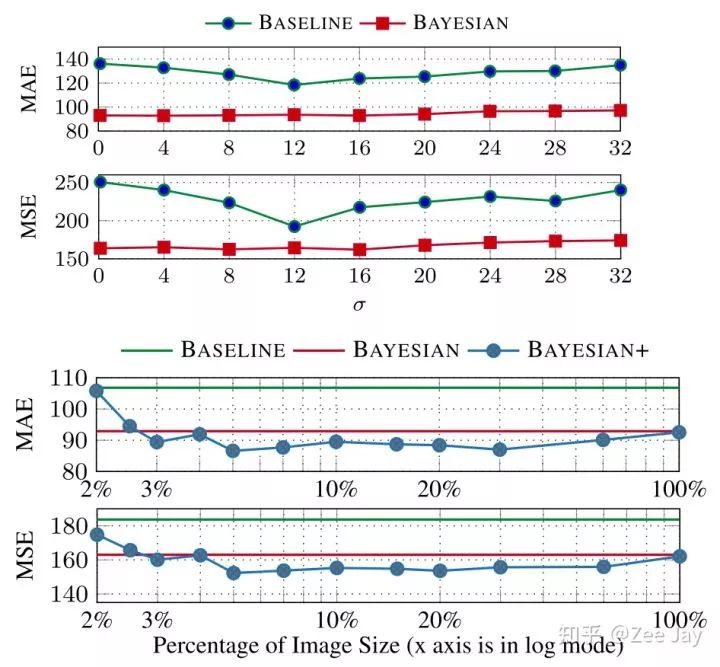
baseline就是用VGG直接训MSE进行训练，Bayesian表示不考虑背景的bayesian loss，Bayesian+表示考虑了背景的loss

可见对于稀疏的部分，加了bayesian loss，定位地更好，加了背景约束，效果比不加背景好

σ和d的影响：

backbone的影响：

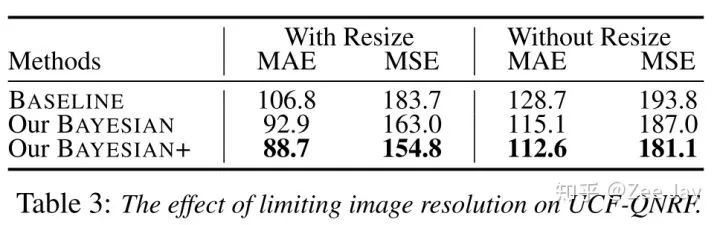
QNRF是否resize的影响：

（5）模型泛化能力

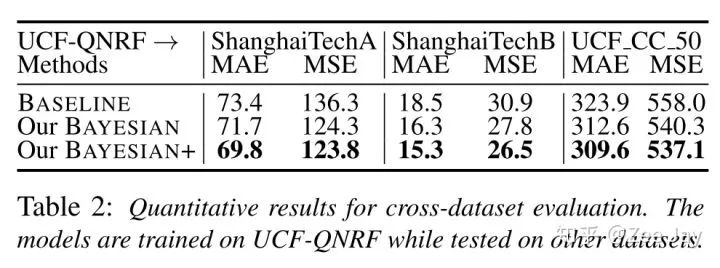
可见在QNRF上训练，在SHA上可以获得不错的泛化能力，但是在SHB和UCF_CC_50上还是一般

4.Comment

本文不愧是Oral的paper，角度很独特，而且数学逻辑非常清晰，虽然看似只是加了一个loss，但是从数学上很合理地证明了其可行性，而且文章确实也写的很好。

重磅！CVer-人群计数交流群已成立

扫码添加CVer助手，可申请加入CVer-目标检测、图像分割、目标跟踪、人脸检测&识别、OCR、姿态估计、超分辨率、SLAM、医疗影像、Re-ID、GAN、NAS、深度估计、自动驾驶、强化学习、车道线检测、模型剪枝&压缩、去噪&去雾&去雨、风格迁移、遥感图像、行为识别、视频理解、图像融合、图像检索等群。一定要备注：研究方向+地点+学校/公司+昵称（如人群计数+上海+上交+卡卡）

▲长按加群

▲长按关注我们

麻烦给我一个在看！