基于LDA的主题模型实践（一）

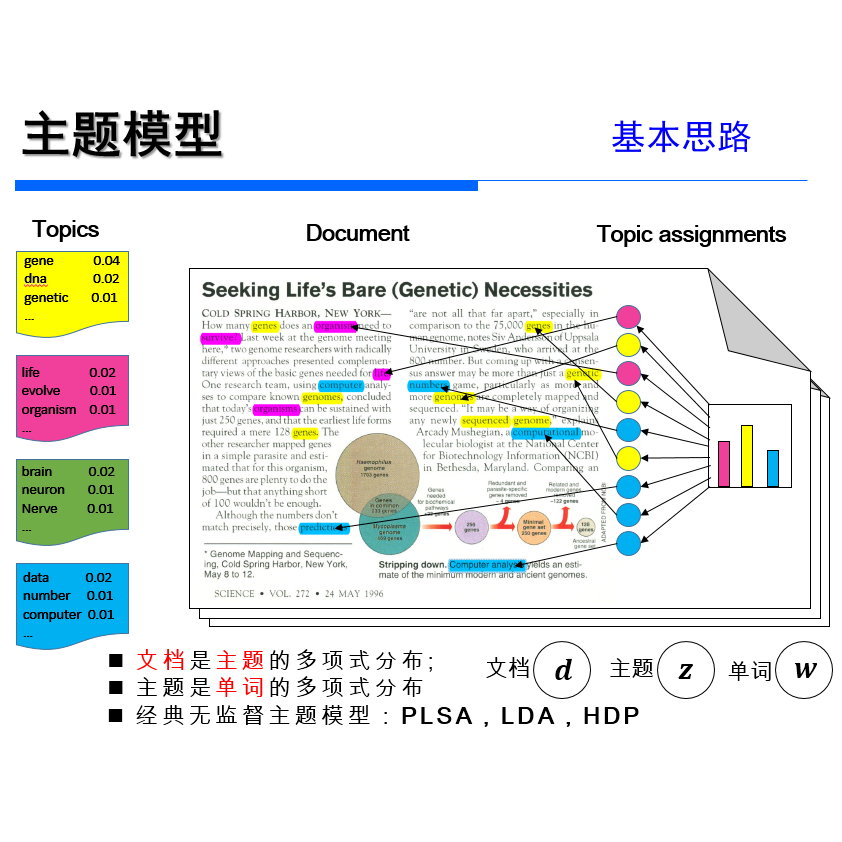
LDA（Latent Dirichlet Allocation）是一种文档主题生成模型，也称为一个三层贝叶斯概率模型，包含词、主题和文档三层结构。所谓生成模型，就是一篇文章的每个词都是通过“以一定概率选择了某个主题，并从这个主题中以一定概率选择某个词语”这样一个过程得到。文档到主题服从多项式分布，主题到词服从多项式分布。

同时，LDA也是一种非监督机器学习技术，可以用来识别大规模文档集或语料库中潜藏的主题信息。它采用了词袋的方法，这种方法将每一篇文档视为一个词频向量，从而将文本信息转化为了易于建模的数字信息。每一篇文档代表了一些主题所构成的一个概率分布，而每一个主题又代表了很多单词所构成的一个概率分布。

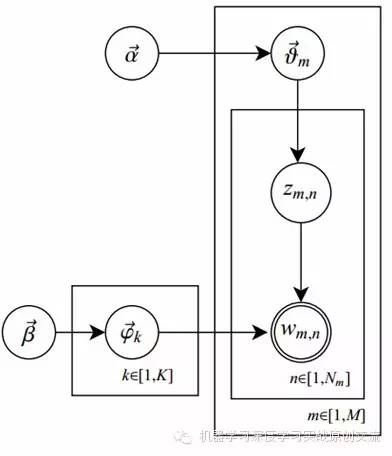
如何理解LDA的训练过程呢？我们假设，语料库中有m篇文章，一共涉及了K个Topic，每个Topic下的词分布为一个从参数为β的Dirichlet先验分布中采样得到的Multinomial分布（注意词典由term构成，每篇文章由word构成，前者不能重复，后者可以重复）。每篇文章的长度记做Nm，从一个参数为α的Dirichlet先验分布中采样得到一个Multinomial分布作为该文章中每个Topic的概率分布；对于某篇文章中的第n个词，首先从该文章中出现每个Topic的Multinomial分布中采样一个Topic，然后再在这个Topic对应的词的Multinomial分布中采样一个词。不断重复这个随机生成过程，直到m篇文章全部完成上述过程。这就是LDA的过程。

在这一次的分享中，由于涉及数学理论概念比较多，因此公式有点多。主页君偷懒索性大部分公式都用图片格式^_^。

定义：

o字典中共有V个term，不可重复，这些term出现在具体的文章中，就是word；

o语料库中共有m篇文档d1,d2…dm；

o对于文档di，由Ni个word组成，可重复；

o语料库中共有K个主题T1，T2…Tk；

oα，β为先验分布的参数，一般事先给定：如取0.1的对称Dirichlet分布；

oθ是每篇文档的主题分布：对于第i篇文档di，它的主题分布是θi=(θi1, θi2… ,θiK)，是长度为K的向量；

o对于第i篇文档di，在主题分布θi下，可以确定一个具体的主题zij=j，j∈[1,K]；

oψk表示第k个主题的词分布：对于第k个主题Tk，词分布φk=(φk1, φk2… φkv)，是长度为v的向量；

o由zij选择φ zij，表示由词分布φ zij确定word，从而得到wix；

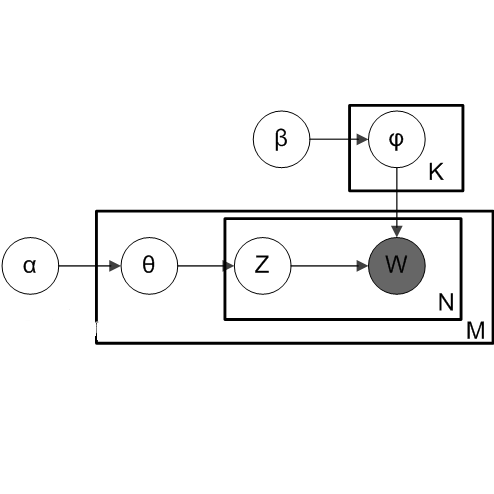
o图中K为主题个数，M为文档总数，Nm是第m个文档的单词总数。β是每个Topic下词的多项分布的Dirichlet先验参数，α是每个文档下Topic的多项分布的Dirichlet先验参数。zmn是第m个文档中第n个词的主题，wmn是m个文档中的第n个词。两个隐含变量θ和φ分别表示第m个文档下的Topic分布和第k个Topic下词的分布，前者是k维(k为Topic总数)向量，后者是v维向量（v为词典中term总数）

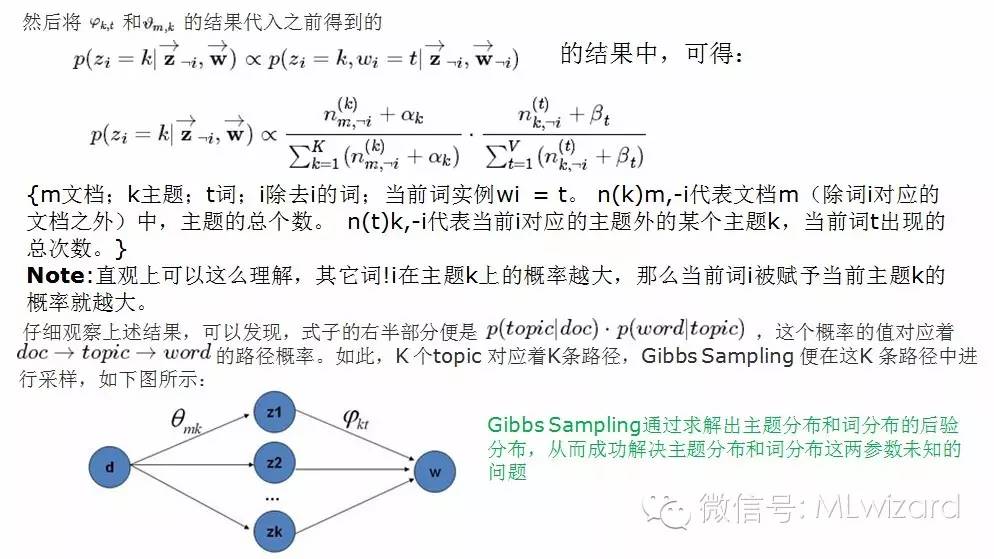
推导过程：

经过前面艰辛推导，我们得到了在满足约束条件下求解目标的迭代公式，那么该如何具体求解，如何求出我们想要的P(z|w)呢？方法有不少：直接求解、EM求解，吉布斯采样法；这里我们采用的是吉布斯采样法，处于文章篇幅限制，先就此打住，关于MCMC-Gibbs Sampling我们放在（二）中来分享。