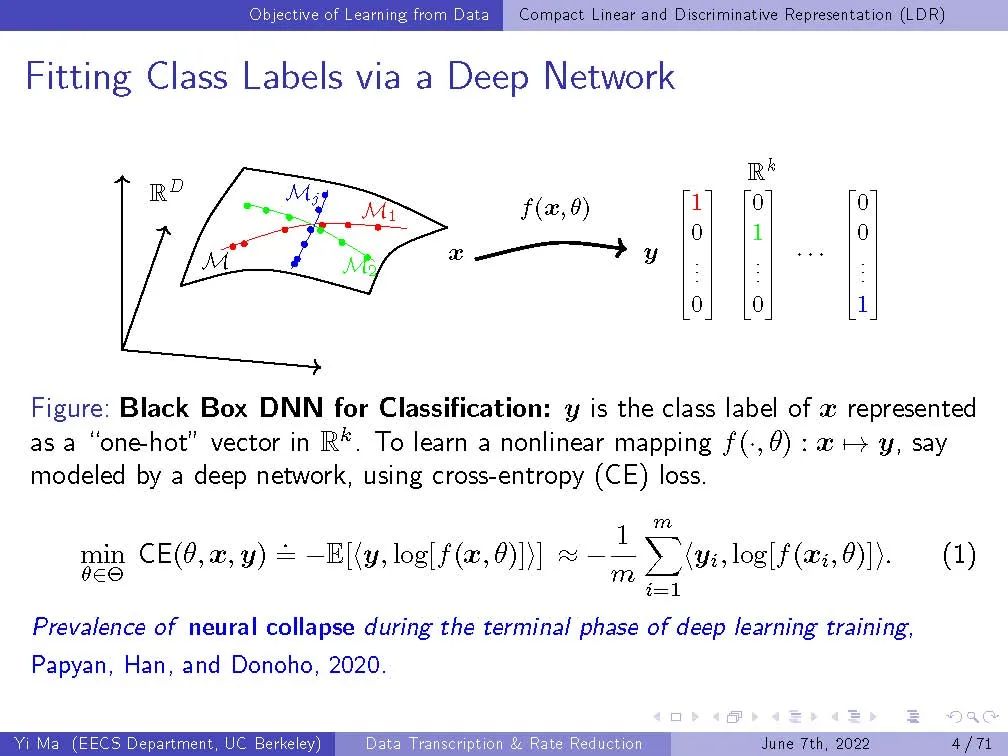
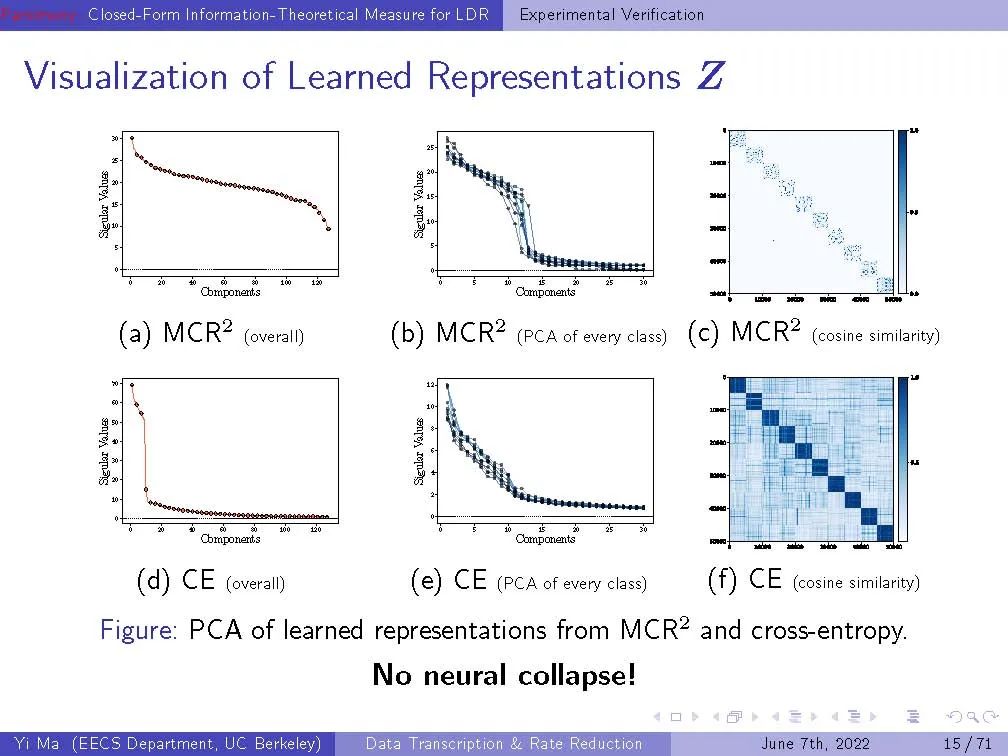
【马毅老师ICASSP2022报告】闭环数据转录通过最小化速率降低

这项工作提出了一种新的计算框架，用于学习真实数据集的显式生成模型。更具体地，提出在由多个独立线性子空间组成的特征空间中学习多类多维数据分布与线性判别表示(linear discriminative representation, LDR)之间的闭环转录。我们认为最优的编码和解码映射可以表示为编码器和解码器之间的一个二参与者极大极小博弈的平衡点。这个博弈的一个自然效用函数是所谓的速率降低，这是一个简单的信息论度量特征空间中子空间类高斯混合之间的距离。该公式的灵感来自于控制系统的闭环误差反馈，避免了昂贵的评估和最小化数据空间或特征空间中任意分布之间的近似距离。该模型在很大程度上统一了自编码和GAN的概念和优点，并自然地将其扩展到学习多类、多维真实世界数据的区分性和生成性表示。我们在许多基准图像数据集上的广泛实验证明了这种新的闭环公式的巨大潜力:我们注意到，不同类的如此学习的特征被明确映射到特征空间中近似独立的主子空间;通过子空间中独立的主成分对每个类中的不同视觉属性进行建模。这项工作打开了许多关于在高维空间中学习子流形的深度数学问题，并提出了关于记忆如何通过纯粹的内部闭环过程形成的潜在计算机制。

https://2022.ieeeicassp.org/view_event.php?mid=70

个人主页：https://people.eecs.berkeley.edu/~yima/

马毅（Yi Ma）为加州大学伯克利分校电气工程与计算机科学系教授。他的研究兴趣包括 3D 计算机视觉、高维数据的低维模型、可扩展性优化和机器学习，近来的研究主题包括大规模 3D 几何重构和交互以及低维模型与深度网络的关系。

视频：

https://archive.org/embed/Redwood_Center_2021_12_02_Yi_Ma

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“CLDT” 就可以获取《【马毅老师ICASSP2022报告】闭环数据转录通过最小化速率降低》专知下载链接

                       

专知，专业可信的人工智能知识分发 ，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取100000+AI(AI与军事、医药、公安等)主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取100000+AI主题知识资料