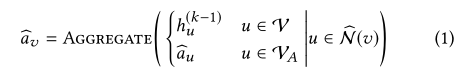KDD20 | 图神经网络的无冗余计算

论文专栏： 图神经网络的聚合优化

论文解读者： 北邮 GAMMA Lab 硕士生  江训强

题目： 图神经网络的无冗余计算

会议： KDD2020

论文地址： https://dl.acm.org/doi/abs/10.1145/3394486.3403142

推荐理由： 对于图神经网络中重复信息的聚合，这篇文章提出了一种简单有效的层次化聚合的方法(HAG)，用于层次化管理中间结果并减少图神经网络在训练和推断过程中重复计算。 HAG 能够保证在计算层次化聚合的过程中，可以使用更少的时间用于训练并且得到的结果和传统的图神经网络模型一致。

1 引言

GNN在单层中基于递归邻域聚合方案，每个节点聚合其邻居的特征，并使用聚合值更新其自身的特征。 这样递归地传播多次（多层），最后，GNN中的每个节点都会从其k阶网络邻居中的其他节点收集信息。 最后GNN层的激活然后被用于下游预测任务，例如节点分类、图分类或链路预测。 然而，如何设计一个能够有效处理大规模图数据集的GNN仍然是一个挑战。 特别的是，许多当前的工作是使用整张图的拉普拉斯矩阵，这样即便是对于中等规模的图，也会面临存储空间的问题。 GraphSAGE首次提出使用对每个独立节点执行小图邻域采样，然后再聚合这些节点的邻域信息，但是对于单个节点进行邻域采样是一个高复杂度的事情，因此许多手工调整的启发式算法被用来限制采样复杂性并选择邻域图并通过优化图的采样步骤来提高GNN的效率。

2 方法

针对两个节点的邻居之间存在显著重叠的时候，在计算单个节点的过程中会有冗余计算。 本文通过减少图中的重叠和冗余的计算，这样能够缓解随着GNN的扩展过程中带来的冗余计算，从而避免这些冗余聚合从而加速GNN的训练和推理。 简单的例子如图1所示:

图1  GNN 与 等价HAG 的比较： (a) 输入图; （b）单层GNN的计算图模型； (c) 避免冗余计算的HAG。 图(b) 中GNN图通过聚集节点 的邻居信息得到节点 的表示 ，所以GNN进行两次冗余计算(即{A,B}和{C,D}两次聚合)。 图(c) 中通过指定生成公共的计算邻居，HAG能够避免重复的计算从而提高模型的计算速度。 例如，就像在图(b)中需要10次聚合的过程，但是HAG仅仅只需要6次聚合就能够达到相同的计算效果。

本文的目标是在训练过程中层次化地组织和使用中间聚合结果，从而降低GNN生成表示过程的冗余。 对于一个HAG而言，表示为 ，节点为 ，边为 , 其中 是原有图的节点并且 表示中间聚合节点集。 以图1(c)为例，聚合节点AB和CD分别为节点{A, B}和{C, D}的中间聚合结果，也即  。传统的GNN表示可以认为是HAG的一个特例， 即   ，因此HAG能够描述当前大部分已存在的GNN模型。 当前的GNN模型在聚合侧可以分为两大类：

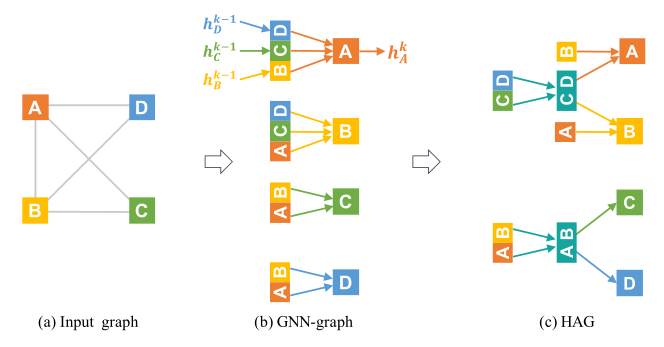
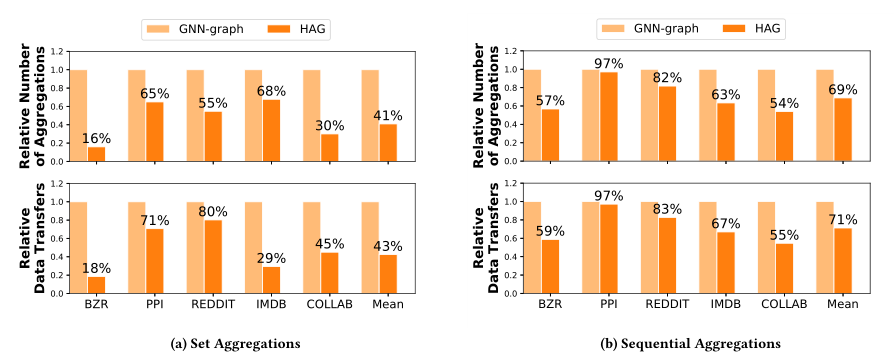
1. Set Aggregate: 大部分GNN都会假设节点的邻居是无序的，并且聚合是关联和交换的操作，这些操作和聚合的执行顺序是没有关系的。在表一的示例中有表示summation aggregation的GCN和element-wise aggregation的GraphSAGE-P。注意，GNN中的set aggregation的过程顺序是不会发生变化的，因此是可以按照HAG对其进行分层聚合。

2. Sequential Aggregate：另一类GNN需要对节点的邻居进行特定的排序，并且对应的聚合顺序是不可以交换的。例如表一中N-ary Tree-LSTM和GraphSAGE中的LSTM变体。HAG可以通过识别相同的节点序列集合，聚合这些节点。

模型按照下面的方式进行聚合：

HAG为了捕捉中间聚合节点的表示，首先定义了一个递归方程(1)来表达 ：

以图1(c)所示，计算 过程中，先根据方程(1)计算出 和 ，然后再依据第5~6行聚合中间结果更新节点A表示。

2.1 GNN with HAG

1. 使用了HAG的GNN和传统GNN的唯一区别在于如何计算每一个GNN的领域聚合的过程(即 )，在聚合过程中，该文章增加了一个步骤用来存储常用的中间聚合的结果，用以减少冗余的计算，即为algorithm1的第3~4行。

2. 同时，该文证明了使用HAG进行中间聚合的GNN和原始GNN会有完全相同的输出和梯度。当GNN模型在每层的输出相同的激活表示 且在GNN进行反向传播的过程当中所有的训练参数都保证了相同的计算梯度，那么与原始GNN和GNN with HAG二者就是等价的。

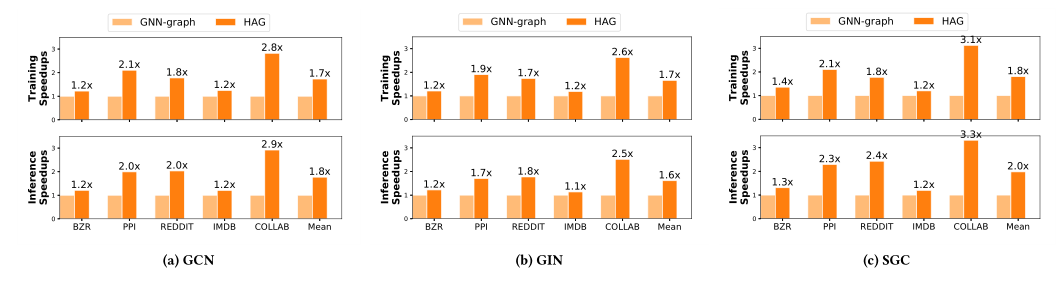
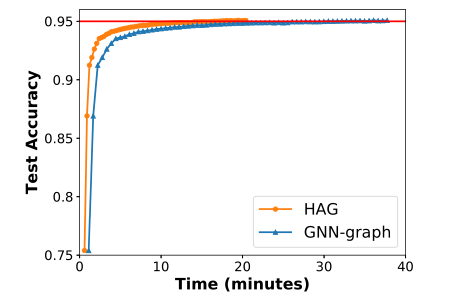
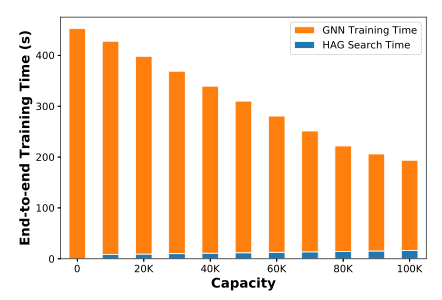
3. 尽管在训练过程中，加入了新的中间节点 ，这个内存的开销也近乎可以不用考虑，实验证明这部分开销仅占原始的开销的0.1%，同时能够将训练的速度提高2.8倍。

2.2 HAG search algorithm

提出了用于优化网络结构的方案，用于生成图1(b)到(c)的转换过程。 首先，需要知道在GNN聚合的过程当中，哪部分所占的开销是最大的，因此得到在聚合过程的cost function如下所示：

 

其中， 是由输入图决定的，也即图1(a)； 和 分别代表聚合和更新的时间开销，这部分开销和GNN本身有关。 因此可以看出优化的目标是降低 ，因此只需要降低该值就能够降低模型整体的时间开销。

algorithm3通过搜寻在聚合过程中重复使用的节点，并将其记录下来，根据其重合的程度因此加入 ，同时对输入图的边进行删减和增加，可以发现 下降， 上升，从而降 降低 ,使得模型复杂度下降。

3 实验

为了验证HAG生成的表示能够保持GNN的预测性能，且具有更好的运行性能。 实验在5个现实世界的图数据集来验证模型的运行性能。 本文在三个维度来验证HAG的性能： a）端到端的训练和推理性能； （b）聚合的数量； （c）数据传输的大小。 数据集规模如下：

3.1 End-to-End Performance

图2 GNN和HAG在两个预测任务、五个数据集和三个不同GNN架构上的端到端运行时性能比较，结果显示在GCN[14]、GIN[24]和SGC[22]上测量每个epoch的训练时间和推理时间。 实验结果显示HAG在不同的实验设置下都提供了显著的性能的加速

与 原始GNN图相比，HAG在保持相同的模型精度的前提下，可以分别提高3.1倍和3.3倍的训练和推理性能。 本文注意到这种改进是完全自动实现的，并且计算HAG是高效的。 因此，由于HAGs提供的改进保持了原始模型的精度，因此没有理由不使用HAG而是原始GNN图。

图3 在Reddit数据集上训练2层GCN模型的HAG图和GNN图的时间精度比较

实验证明了使用HAG表示的GCN模型能够在每个epoch结束之后达到完全相同的训练和测试精度。 经过55个训练周期，HAG和GNN图的测试准确率均达到95%，HAG使端到端训练时间提高了1.8倍。

3.2 Aggregation Performance

图4 比较聚合操作的数量和GPU线程之间传输的总数据以执行聚合（越低越好）。 y轴由GNN图的聚合数量执行规范化，每个图的最后一列是所有数据集的几何平均值。

图4显示了比较结果。 对于具有集合聚合的GNNs，HAG将聚合数减少1.5-6.3倍，数据传输量减少1.3-5.6倍。 对于具有顺序聚合的gnn，HAGs将聚合和数据传输分别减少1.8倍和1.9倍。 对于集合聚合，性能改进更为显著。 由于集合的排列不变性，集合的最优性比序列聚集包含更多的潜在冗余。 因此，尽管最优解更难计算，但是对于集合聚合，HAG可以获得更高的性能。

3.3 HAG Search Algorithm

图5 使用不同容量(即 )的HAGs对COLLAB数据集进行端到端GCN训练时间。

搜索算法使用超参数能力来控制HAG中聚合节点的数量。 更大的容量允许算法消除更多的冗余聚合，并实现更低的成本。 图5显示了使用不同容量的HAG在COLLAB数据集中的端到端GCN训练时间。 较大的容量值可以持续改善训练绩效，这说明成本函数是评估和比较不同HAG的合适指标。 通过逐步增加容量，搜索算法最终找到一个具有∼100K个聚合节点的HAG，它消耗6MB内存（0.1%的内存开销），同时将训练性能提高2.8倍。 此外，与端到端的训练时间相比，HAG搜索时间可以忽略不计。

4 结论

本文引入HAG，一种新的图表示来消除许多GNN中的冗余。 本文提出了一个代价函数来估计不同HAG的性能，并使用搜索算法来寻找优化的HAG。 通过提高端到端的训练性能和减少GNN训练中的聚集和数据传输，HAG的性能优于现有的GNN图。

本期责任编辑：杨成

本期编辑：刘佳玮

---

北邮 GAMMA Lab 公众号

主编：石川

责任编辑：王啸、杨成

编辑：刘佳玮

副编辑：郝燕如，纪厚业

长按下图并点击“识别图中二维码”

即可关注北邮 GAMMA Lab 公众号