随机漫步的金融交易员
1900年,法国数学家 Louis Bachelier 首次开创性的描述了随机过程(stochastic process),它表示的是一种随时间推移而出现的随机波动的数学过程。后来在金融建模的背景下,它被称为布朗运动(Brownian motion)。
与流体中的粒子所作的布朗运动一样,随机行为也能用分子运动论(Kinetic Theory of Molecules)来理解。分子运动论描述的是在气体或液体中,粒子之间的频繁相互碰撞而引起的随机运动,从而导致了物理布朗运动。在这种方法中,我们可以从微观交互(或碰撞)模型开始,将其构建到宏观框架中。最终会得到一个方程,例如玻尔兹曼方程或朗之万方程,用以描述粒子的位置、温度或其他一些大尺度统计变量随时间的演变。特别值得一提的是,Bachelier 的发现比爱因斯坦发表他的第一篇关于物理布朗运动的论文(1905)还要早五年。
在过去100多年以来,物理学和金融学布朗运动间的神秘相似性已引起了科学家们广泛关注。金融布朗运动一词描述了市场价格是如何像布朗运动一样,看似不规则的随着时间的推移变化。
○ 研究人员利用个人金融交易员的活动数据,设计了一个可用于理解宏观市场趋势的微观金融模型。| 图片来源:APS/Alan Stonebraker
经济物理学家试图为这种不规则跌涨起伏的金融系统也研究出一套分子运动论。现在,物理学家已经证明,随机漫步(random walk)的模型可以捕捉到宏观的市场动态,例如道琼斯工业平均指数(股票价格平均指数)的变化。但一直以来,由于缺乏与个体交易员有关的微观行为数据,从而并没有一个能描述微观交互作用的模型。
现在,得益于大数据和统计物理学的力量,日本东京工业大学的研究人员利用高频货币兑换中个体交易员的数据,构建了一个这样的微观模型。物理学的世界与金融学世界又互相靠近了一步。这是一个利用不同金融交易员的活动数据,设计出一个可解释宏观市场趋势的微观金融模型。这一模型成功地反应了流体中粒子的随机运动(布朗运动)与金融市场的价格波动(金融布朗运动)之间的紧密相似性。研究成果发表在了《物理评论快报》上。研究人员基于直接的观测数据和理论分析,阐明了金融布朗运动会如何浮现于金融市场的微观动态中。
在新的研究中,统计物理学家 Kiyoshi Kanazawa 和他的团队利用一个开放于2016年7月的数据库,分析了美元-日元市场在一段为期5天时间内的高频交易价值。他们追踪了交易员在“出价”(买入价)和“询价”(卖出价)时的行为。交易员每隔几秒就提交一次订单,但交易只在一个交易员的询价与另一个交易员的出价匹配时发生。Kanazawa 等人发现交易员会根据市场交易价格的变化调整其买卖价格来应对每笔交易。
当进行集体性研究时,研究人员发现这种“趋势跟踪”与物理学中的惯性概念很类似。趋势跟踪行为是指当市场成上升或下降趋势时,个体交易员倾向于因此趋势而对未来价格作出上升或下降的预期。通过模拟这种“趋势跟踪”,研究人员发展出了一套能准确捕捉价格分布和其他市场指标的宏观理论,得出了一个关于整体价格波动的类波尔兹曼方程。他们认为,这一植根于标准物理学的模型为了理解稳定金融市场的价格波动提供了坚实的基础。
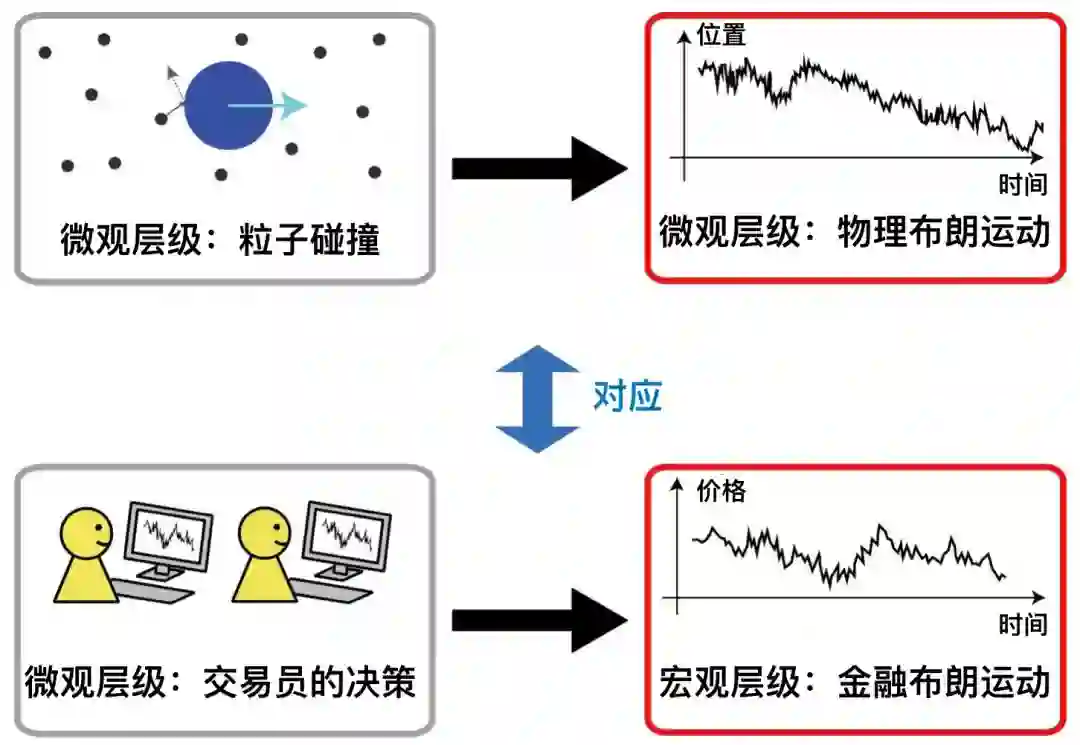
○ 分子运动论涉及粒子间的相互碰撞,导致物理学上布朗运动的出现(上图)。通过分子运动论框架的类推,由个体交易员作出决策而造成金融布朗运动的出现(下图)。| 图片来源:Kiyoshi Kanazawa/东京工业大学
接下来,Kanazawa 和同事们还希望这一模型用于不稳定市场的研究。不稳定市场易受外部冲击的影响,是一个极具挑战性的研领域,需要更好地了解交易员应对不同冲击会如何反应,以及如何将这种行为反映在理论模型中。
研究人员表示:“我们坚信,随着大数据分析等技术的突破,金融市场将是需要硬科学来攻克的一个绝好课题。”
编译:椰叶
参考链接:
https://arxiv.org/abs/1802.05993
https://www.eurekalert.org/pub_releases/2018-03/tiot-tpo032818.php
https://physics.aps.org/synopsis-for/10.1103/PhysRevLett.120.138301
本文经授权转载自《原理》微信公众号
1.送别郝柏林先生
END