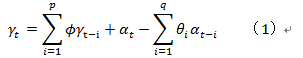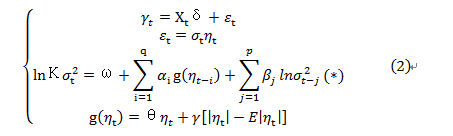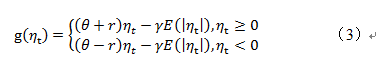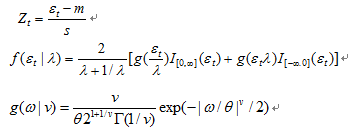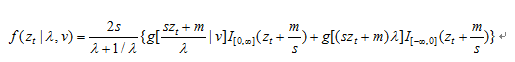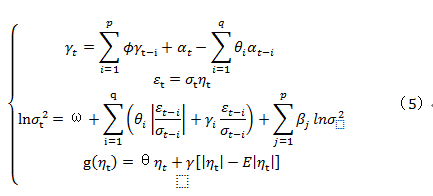R语言金融波动率建模|基于SGED分布的变参数ARIMA+EARCH动态预测模型的研究

     

作者简介Introduction

齐祥会：某高校小硕一枚，“中金所杯”全国高校金融衍生品竞赛二等奖获得者，通过FRM（金融风险管理师）考试， 获得过全国赛、省赛、校赛量化投资团体赛及金融建模等前三等奖项，即将就职于某期货公司投资研究部，研究方向为股指期货、国债期货等，热爱使用R语言金融统计建模及可视化分析，希望能与行业大神有更多学习交流的机会！  

 基于SGED分布的变参数ARIMA+EARCH动态预测模型的研究

 —以沪深5只个股的滚动预测为例

本文代码请在公众号后台回复：R语言波动率金融建模  获取

【摘要】根据股票市场收益率序列呈尖峰厚尾、偏态、波动集聚和杠杆效应等特征,本文构建Skew-GED(SGED)分布下的变参数ARIMA+EGARCH动态混合预测模型来挖掘和分析收益率序列的内在规律，运用r语言通过实时最优化动态模型的参数估计，分别对5只股票日对数收益率序列的未来收益情况进行每日预测每日更新，输出交易信号；最后通过滚动时间窗进行推进分析，解决可能存在的过度拟合问题，结果表明动态模型能更好地描述收益率特性，提高预测准确性。

【关键词】变参数ARIMA+EGARCH动态模型；参数优化；推进分析；股票收益率预测

一、引言

波动性是股票市场最为重要特性之一，因此，探讨其波动规律、把握其运行趋势成为当今学术界与实务界研究的热点。

股票收益率波动模型的研究主要有：ARMA 类模型、ARCH 类模型及二者的混合模型，模型中波动误差分布的假定主要有正态分布、T 分布、GED 分布和SKT 分布。国内外大量研究表明，收益率序列波动通常具有集聚性、分布的尖峰厚尾性以及有偏性。本文以5只股票为例，通过对股票日对数收益率序列的分析，发现股票日对数收益率波动存在明显的“尖峰厚尾”现象、波动集聚和非对称特征。通过建立收益率序列的ARIMA 模型处理中期记忆特征，然后再利用EGARCH模型处理异方差的非对称以及波动率聚集特征，采用S-GED分布解决股票收益率波动的“尖峰厚尾”现象以及有偏分布问题，就能够很好地解决股票收益率的这些特性，取得较理想的拟合及预测效果。

本文利用Skew-GED(SGED)分布下的变参数ARIMA+EGARCH动态预测模型对给定的5只股票收益率进行预测，为股票收益率预测和股票投资提供一种思路。任何一种预测方法都要回归现实，接受实践的检验，本文的预测部分证明了该模型具有一定的预测精度，在一定程度上能够为投资者和金融市场相关人员及机构提供决策依据。

二、股票收益率预测建模

2.1模型建立原理

2.1.1进行股票收益率的预测

在股票市场中，准确的股票收益率预测是市场交易各方共同关心的重要问题。多数金融研究针对的是资产收益率而不是资产价格。Campbell，Lo和MacKinlay（1997）给出了使用收益率的两个主要理由：第一、对普通投资者来说，资产收益率完全体现了该资产的投资机会，且与其投资规模无关；第二，收益率序列比价格序列更容易处理，因为前者有更好的统计性质。本文对上述各个指数的对数收益率进行分析和预测。

2.1.2 ARIMA+EGRACH混合模型构建

由于影响股票市场的因素十分复杂，仅靠建立单一的股票收益率预测模型来提高预测精度是非常困难的。本文提出了ARIMA+EGRACH模型运用滚动时间窗口来提高股票收益率预测精度的新思路。首先，ARIMA模型能有效地处理金融时间序列的记忆特征；其次，由于GARCH模型中，正的和负的冲击对条件方差的影响是对称的，因此GARCH模型不能刻画收益率条件方差波动的非对称性。故本文选用改进后的EGARCH模型来挖掘和分析预测收益率序列的内在规律。通过使用ARIMA模型构成EGARCH模型中均值方程，由此构成 “ARIMA+EGRACH”模型，并通过滚动时间窗参数估计的持续最优化，以期提高预测精度.

（1）对个股对数收益率序列建立一个变参数的ARIMA（p，d，q）模型

一般的ARMA（p，q）模型的形式为：

 如果把ARMA模型广到允其AR多项式以1作为它的单位根，则模型就变成了众所周知的自回归就和滑动平均（ARIMA）模型，如果存在单位根，则模型非平稳，若不存在单位根个模型平稳。

（2）对个股对数收益率及个股价格波动率构建一般的EGARCH模型

EGARCH模型是指数GARCH模型，是不要求非负的限制的一种模型，能对正负扰动项进行非对称处理。 EGARCH模型是放松了对GARCH模型的参数非负约定。

股票价格的波动常常表现为杠杆效应现象。相同单位的利空消息对波动的影响常常比利好消息来得大，这种非对称影响称为杠杆效应，因而EGARCH模型能有效地分析杠杆效应。

为了反映金融市场波动的非对称性，Nelson（1991）提出了EGARCH模型，对均值方程和波动率方程进行联合估计，可以表示为

用分段函数重新表示，容易看出其非对称性：

        

式中，当时，说明干扰对股价的影响是非对称的；当时，说明金融产品价格波动受负外部冲击的影响大于受正外部冲击的影响，而此时的被称为杠杆效应。在实际应用中一般将式（*）简化为

（3）大量的金融实证研究表明，金融市场的时间序列具有尖峰厚尾、有偏的特征。为了更好解决尖峰后尾问题，许多学者使用了t 分布和GED分布，都增强了模型对金融数据的刻画能力。但是这些分布属于对称分布，依然不能有效刻画数据的有偏特征；同时，由于偏度和峰度并不是完全独立，因此，对于股票价格序列的分析客观上要求采用可以刻画尖峰厚尾、有偏特征的分布进行分析。

为了刻画这种非对称性，国外提出了一些前沿的分布来解决这样的问题。Fernandez和steel提出了将任意一个单峰、对称分布转变成偏态分布的一般方法。S-GED分布作为GED分布的扩展，它是在GED分布基础上加入一个偏态参数λ得到的。其定义如下：

其中这里，

   ，是伽马函数。

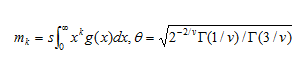
如果序列满足上述3项条件，并且均值为0，方差为1，则其服从一个标准的S-GED。

Zt分布可以写成：

当偏度指标时，其表示的是一种对称的分布函数形式；当时，表示该分布是左偏的；当时，表示分布右偏。参数控制收益分布尾数“胖瘦”程度。在条件下，当时，尾部比正态更厚，当时，SGED分布退化为正态分布；当时，尾部比正态更薄。本文利用SGED来综合刻画股票收益率的“有偏”和“厚尾”特征。

（4）联立ARIMA模型及EGRACH模型                     

通过使用ARIMA模型构成EGARCH模型中均值方程，得到以下的联立方程:

2.2 ARIMA+EGRACH模型参数设定

 2.2.1 ARIMA模型参数设定

（1） ARIMA（p,d,q）过程涉及p，d，q三个参数的设置，其中d代表使得原时间序列平稳时所做的差分次数，要对所选的5只个股股票对数收益率进行预测，首先检验各自的对数收益率序列平稳性，对于股票收益率的ARIMA（p,d,q）过程中d常取0，本文也在之后进行实证检验说明取d=0的合理性。实质上，此时的ARIMA（p,0,q）过程等同于ARMA（p,q）过程。

（2）ARIMA（p,d,q）过程p是自相关截尾数，q是偏自相关的截尾数。关于p、q参数的选择，本策略使用R软件进程序自动最优选择，先设定p、q的大致范围0到5，再通过R程序语言使用AIC信息准测选择出能使AIC最小的p、q值。

2.2.2EGRACH模型参数设定

股票收益率具有平稳性特征,存在波动集聚性,具有显著尖峰后尾特征,日对数收益率序列存在ARCH效应,收益率的波动具有明显的杠杆效应。通过比较,得出EGARCH(1,1)模型最能模拟股票日收益率的波动实际。因此参数设定为（1,1）。

三、基于ARIMA-EGRACH模型的股票收益率预测实证

                         

3.1 数据来源

本文用R软件从雅虎财经网（http://finance.yahoo.com）和wind金融数据库在线提取大赛主办方给定的5只股票的日行情数据如下：    

3.2股票收益率的数据处理

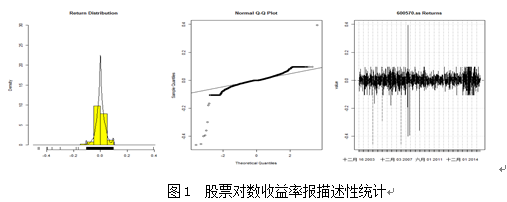
3.2.1股票收益率图形分析——以600570.ss为例

从股票的收益率时序图中可以看出：股票收益率具有波动集聚和杠杆效应。

从股票的收益率分布图中可以看出：股票收益率具有尖峰厚尾、偏态特征。

从股票的收益率QQ图中可以看出：股票收益率分布均非正态分布。

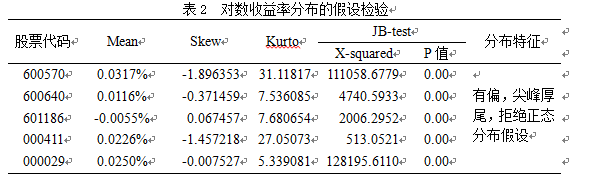
3.2.2对数收益率的描述统计

通过进一步观察对数收益率的描述统计量和JB检验可以看出：5只股票的对数收益率均呈现有偏，尖峰厚尾的特征，并且JB检验的p值均小于1%，拒绝正态分布假设，即5只股票的对数收益率分布均非正态分布。

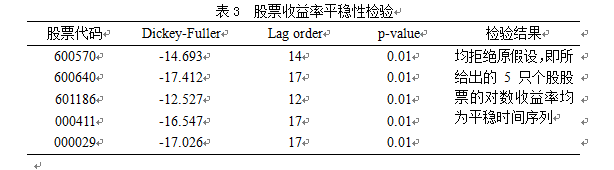
3.2.3股票收益率平稳性检验

通过对数收益率平稳性检验，得出5只个股股票的对数收益率均为平稳时间序列，即ARIMA（p,d,q）过程中d=0。

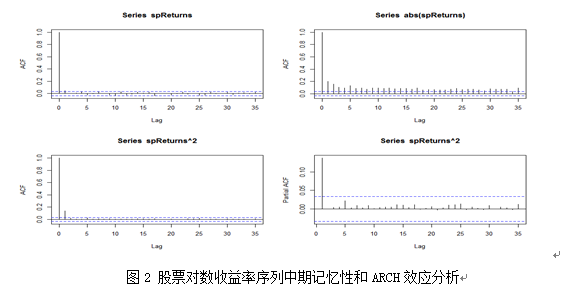
3.2.4股票收益率序列中期记忆性检验——以600570.ss为例 

如图所示，收益率序列和收益率绝对值序列均序列相关，即需要用ARMA解决中期长记忆性，同时，由Box-Ljung检验结果p值为0.02375，拒绝原假设，也可以看出序列存在中期长记忆性；从图3和图4可以看出，序列存在异方差。

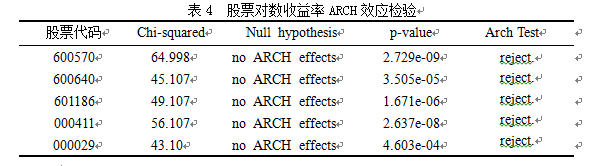
3.2.5股票收益率GARCH效应检验

由ARCH效应检验结果可以看出，序列存在明显的ARCH效应

综上，单独用ARMA模型或单独用GARCH模型拟合数据都是不充分的，需要将二者结合起来进行建模。

3.3变参数ARIMA+EGARCH动态预测模型实证

此处以500个数据为时间窗为例，重点说明建模过程：

（1）建立滚动窗口长度（windowlength），一年365天的交易日期长度约为250天，故滚动窗口长度从500中择优选取。

（2）建立forecastsvector 来储存股票收益率预测值。

（3）利用循环语句对ARIMA模型中的p，q参数进行择优，范围为（0,5），即在25种组合中以AIC值作为判断依据找出最优参数，即利用编程程序进行自动参数优化。

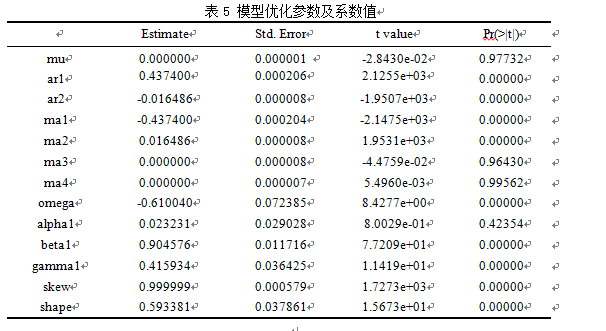
   这里以600570.ss为例，参数优化结果：

GARCH Model: eGARCH(1,1)

Mean Model: ARIMA(2,0,4)

Distribution: sged

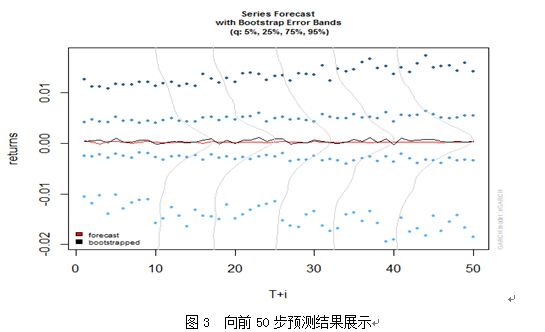
（4）将参数寻优后的ARIMA模型设定为EGARCH（1,1）模型的均值方程，利用组合模型进行后一天股票收益率预测。

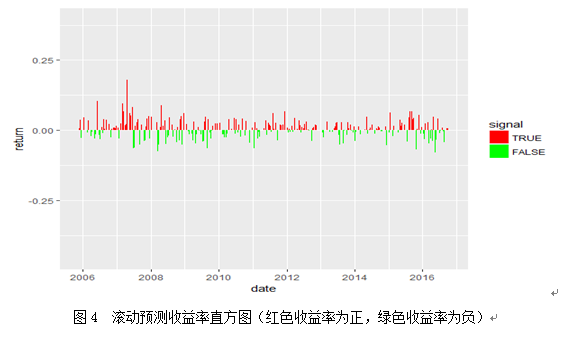
（5）推进分析，本文采用的是动态预测，只进行一期预测，在由实际值预测出第一期的值之后，将第一期真实值和历史数据重新组成新的序列再进行第二期的预测，以此递推。最后将预测值和真实值进行对比。

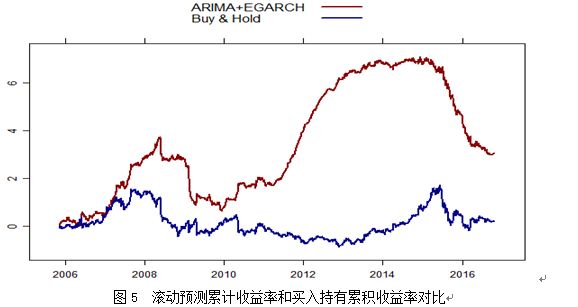
由以上结果可知，直观来看，使用ARIMA+EARCH动态预测模型总体效果较好，滚动预测累计收益率在后期更是远远超过简单的买入持有策略的累积收益率。用下表对ARIMA+EARCH动态预测模型绩效最进一步的评估：

由上表，与简单的买入持股票策略相比ARIMA+EARCH动态预测模型应用下的交易策略获胜率有所提高，同时年化收益率及年化夏普比率也有提高。但同时需要注意的是该策略下回撤率问题并没有得到较好解决，即发生亏损后的最大可能损失还处于较高水平，主要原因是，该动态预测策略重在建模与预测效果，若应用于实盘还需要进行进一步的止损优化。 

四、结论及建议

4.1 结论及意义

本文通过对股票数据统计和计量分析，验证股票对数收益率序列有偏“尖峰厚尾”分布以及波动率聚集、杠杆效应等特征以后，通过分析及建模，选用改进后的基于滚动时间窗的变参数ARIMA+EARCH动态预测模型来挖掘和分析预测收益率序列的内在规律,通过参数实时优化来得到最佳拟合效果，并进行预测，同时；通过滚动时间窗来避免过度拟合的问题等可能影响客观现实的错误干扰，最终通过和买入持有累计收益率对比可知，该模型能很好拟合现实收益率的变化，具有较好的预测效果，可以为投资者和相关人员机构提供一种较好的与预测工具和手段。

4.2 不足及改进建议

（1）由于数据时间周期较长，通过r语言来计算信号和预测耗费很时间，因此本文中选用的参数是实时最优的，但时间窗不一定是最优的时间窗，采用了大多数研究所使用的数据长度来拟合，后续还有待进一步优化。

（2）本文重点在于建模及预测，没有加入止损，若要变为实盘交易策略，还需加入止损操作等风险控制手段以更好服务投资者。

（3）若出现金融危机等极端事件可能存在模型风险，还需辅助其他判断等。

参考文献

[1]EdilbertoCepeda-Cuervo.Generalized EGARCHRandom Effect Models Application to Financial Time Series[J].Communications in Statistics - Simulation and Computation. 2010(8)

[2]RajashreeDash,P.K. Dash.An evolutionary hybrid Fuzzy Computationally Efficient EGARCHmodel for volatility prediction[J].Applied Soft Computing.2016(4).

[3]RajashreeDash,Pradipta Kishore Dash. Prediction of FinancialTime Series Data using Hybrid Evolutionary Legendre Neural Network:Evolutionary LENN[J].International Journal ofApplied Evolutionary Computation (IJAEC). 2016(1).

[4]ZijingZhang,Hong-Kun Zhang.The Dynamics ofPrecious Metal Market VaR: A GARCH-EVT Approach[J].Journalof Commodity Markets.2016(10).

[5]杨瑞成,秦学志.ARFIMA-EGARCH-M模型在汇率收益率波动分析中的应用[J].计算机工程与应用,2009,(45)

[6]杨爱军,肖振宇.基于ARMA-APARCH-SGED模型的原油价格风险度量研究[J]. 统计与信息论坛,2011(8)

[7]（美）RueyS.Tsay.金融时间序列分析[M].王远林，王辉，潘家柱译.北京：人民邮电出版社，2012,9

[8]（美）RueyS.Tsay.金融数据分析导论——基于R语言[M].李洪成，尚秀芬，郝瑞丽译.北京：机械工业出版社，2013,10

[9]蔡立耑.量化投资——以R语言为工具[M].北京.电子工业出版社,2016,1,218-234

　往期精彩内容整理合集　

2017年R语言发展报告（国内）

R语言中文社区历史文章整理（作者篇）

R语言中文社区历史文章整理（类型篇）

公众号后台回复关键字即可学习

回复 R                  R语言快速入门及数据挖掘 
回复 Kaggle案例  Kaggle十大案例精讲（连载中）
回复 文本挖掘      手把手教你做文本挖掘
回复 可视化          R语言可视化在商务场景中的应用 
回复 大数据         大数据系列免费视频教程 
回复 量化投资      张丹教你如何用R语言量化投资 
回复 用户画像      京东大数据，揭秘用户画像
回复 数据挖掘     常用数据挖掘算法原理解释与应用
回复 机器学习     人工智能系列之机器学习与实践
回复 爬虫            R语言爬虫实战案例分享