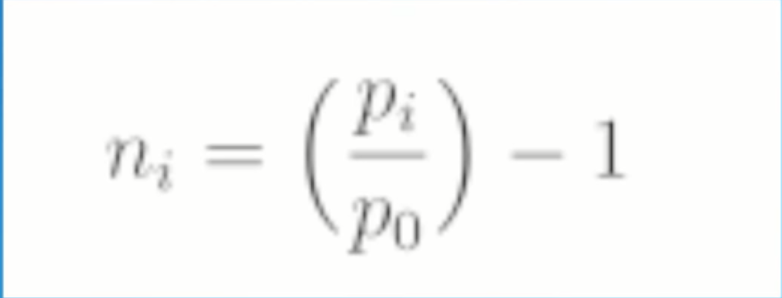视频 | 如何用 AI 预测股价？

会员服务 ·

视频 | 如何用 AI 预测股价？

2017 年 6 月 30 日 AI研习社 雷锋网字幕组

AI 研习社按：今天为大家带来硅谷深度学习网红 Siraj 的一则教学视频：如何用深度学习模型预测股价。（内心OS：终于要开始讲点正经事了！）具体视频内容如下，Github 代码链接详见文末“阅读原文”。

为了照顾没有 WiFi 的小伙伴，我们特别提供了以下根据视频内容整理的文字版（hin 贴心有木有！）：

我们能用机器学习准确地预测股价吗？

一种普遍的说法是股价是完全随机和不可预测的——让一只猴子蒙住眼睛在报纸的金融版面用飞镖选出来的投资组合，也能和投资专家精心选择的一样好。

那么问题来了，为什么像摩根斯坦利和花旗集团这样的顶级公司还要雇佣大量的分析师来建立预测模型呢？

曾几何时，证券交易中心的大厅里挤满了人，全都打了鸡血一样，系着松垮的领带，边跑边冲着电话叫嚷。但是现如今你更可能见到的是成排的机器学习专家，静静地坐在电脑屏幕前。事实上，华尔街大约70%的交易现在是在电脑软件上进行的。欢迎来到算法时代！

发展历史

在金融业，定量分析领域也只有25年历史。即使到现在，它还没有得到充分认可和理解，也没有被广泛应用。它研究的是某些特定的变量与股价形势有何种关联。

在70年代，两位英国统计学家 BOX和Jenkins就利用大型计算机进行了早期尝试。他们能够获取的唯一数据就是价格和交易量。他们给那个模型命名为Arima，当时它运行很慢而且很贵。

但是在80年代事情有了转机。电子表格的发明使得企业能够建立起公司的财务绩效模型，也让数据的自动收集变成了现实，而且随着计算机性能的发展，模型分析数据速度也变得更快。华尔街又迎来了春天。

在过去的几年里，我们看到有许多相关的学术论文出版，它们用神经网络来预测股价而且都取得了不同程度的成功。但是也仅限于专家们有能力构建这些模型。

现在，有了像Tensorflow这样的开源系统，任何人都可以建立起强大的预测模型，这些模型都经过了大量的数据集的训练。

实操练习

用Keras和Tensorflow建立自己的模型

所用数据集

2000年1月-2016年8月每天收盘时的标准普尔500指数（这是一系列以时间顺序展开的数据点或称为时间序列）。

训练目标

任给一个日期就能预测出收盘价。

Step 1 加载数据

用一个常用的数据加载函数，它本质上就是把CSV文件读写到数值数组中然后进行归一化，而不是把那些数据直接输入我们的模型。数据归一化可以提高收敛性。

我们用这个公式对每个值都归一化，以此来反映与起始点的比例的变化，所以把每个价格除(pi)除以初始价格(p0)然后减1，当我们的模型做出预测之后，我们就用这个公式把数据去归一化，再由其得到实际的数据。

Step 2 建立模型

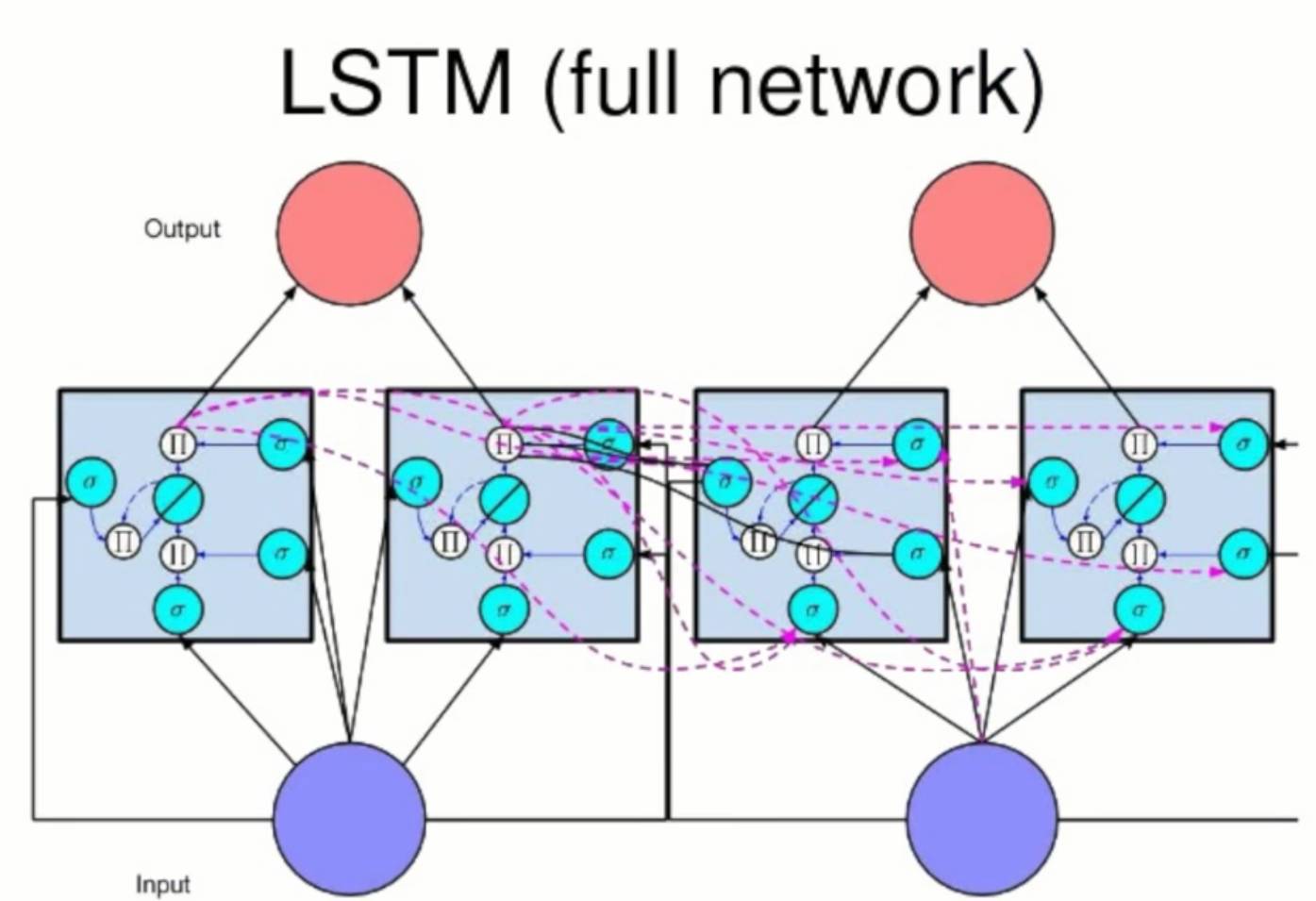
构建模型时，首先把它初始化成序列，这样它才能成为一个线性的堆叠层。然后我们要加上我们的第一层，LSTM层。那么什么是LSTM呢？

LSTM

我们很容易按照先后回想起歌词，但是我们能够倒着把它唱出来吗？不行。

因为我们是按照序列的方式来学习这些歌词的，这是有条件的记忆。我们能想到一个词的前提是我们知道在它之前词是什么，当我们记得顺序时记忆才起作用，我们的思路有持续性，但是前馈神经网络没有，它只接受一个固定大小的向量作为输入。所以我们不能用它来预测一部电影的下一帧，因为某个特定事件发生的可能性取决于它在之前的每一帧图片都发生了什么。所以需要一个图像序列向量作为输入，而不只是一张图片。

我们需要一种方法来存留信息，所以要用RNN（递归神经网络）。递归网络可以输入向量序列。回想一下前馈神经网络的处理，隐藏层的权值仅仅是基于输入数据。但是在RNN中，隐藏层则是基于当前时间步输入的数据和前一个时间步的隐藏层，随着输入数据的增多，隐藏层在不断地变化，并且得到这些隐藏层的唯一方法是输入正确的数据序列。这就是记忆的实现方式而且我们可以对这个过程进行数学建模。

所以任一时间步的隐藏状态都是同时间步输入的数据经过权重矩阵加权后的的函数，这部分与前馈网络的中的隐藏状态类似，然后加上前一个时间步的隐藏态，它是由自身的隐藏态与隐藏态矩阵（或称变换矩阵）相乘得到的，而且因为这个反馈回路在序列的每一时间步都会出现，每一个隐藏态都不仅有前一步的隐藏态相关，而且跟之前所有步的都相关，所以我们称之为递归。

在某种程度上，我们可以把它认为是相同网络的复制，每一个网络都在给下一个网络传递信息，所以这才是递归神经网络高明之处，它们可以把之前的数据与当前的任务联系起来。

但是，我们还有一个问题，先来看一下这一段文字，它以“我希望先辈会注意到我”开头，以“她是我的朋友，他是我的先辈”结尾。如果我们想训练一个模型，给出其他所有的词，它能预测这句话的最后一词，我们需要从这一系列句子最开头部分的上下文，以便确定这个词可能是“先辈”，而不是同伴或同事。

在一个常规的RNN中，记忆逐渐消逝，因为后期的时间步的误差信号在反向传播的过程中还远不能及时地影响到早期的时间步的网络，Joshua Bengio把这叫做消失梯度问题（vanishing gradient problem ），是在他的一篇引用最多的论文中提出的。论文的标题就是“学习带有梯度下降的长期依赖有难度”。对此问题一个普遍的解决方法是对递归网络作一个叫做”长短期记忆（LSTM）”的修正。

通常，神经元是对输入数据的线性组合应用激活函数（如sigmoid函数）的单元。在一个LSTM递归网络中与之相反，用记忆单元来替代这些神经元。每个单元有一个输入门，一个输出门和一个内部状态，内部状态跨过时间步向自身输入常量权重1，这就解决了消失的梯度问题，因为在反向传播过程中任何经过这个自循环单元的梯度都被永久保存下来了，因为误差乘以1值仍然是一样的。

每个门都是一个激活函数，像Sigmoid一样，在前向传递时，输入门学习何时让激活函数传入记忆单元，而输出门学习何时让激活函数传出记忆单元。在向后传递的过程中，输出门学习何时让误差流入记忆单元，输入门学习何时让误差流出记忆单元并传到网络的其他部分。所以，尽管在递归网络中其他的东西都是保持不变。只用这个强大的更新公式更新我们的隐藏层。