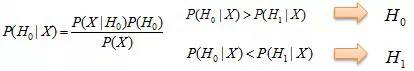【温故】P值之死

2018 年 7 月 8 日 数说工作室

【温故】

100年前的今天（1918年7月8日），有位叫 Ronald Fisher 的人向外界宣读了一篇论文《Thecorrelation between relatives on the supposition of Mendelian inheritance》，这篇论文打开了统计遗传学的大门。

Fisher大神也被认为是P值的第一推手，以及“费雪学派”（Fisherian）的开山宗师。大家知道，统计学的很多早期理论都来源于生物学，这篇论文可以说影响了整个统计学界。

四年前，数说君发布了一篇《P值之死》，很多朋友转发（尽管没有署名），知乎上也有相关讨论

（https://www.zhihu.com/question/24743876/）

今天，重发这篇文章，温故一下关于P值的争论，纪念一下100年前的今天。

【正文】

有一天，我走进统计学的神殿，将所有谎言都装进原假设的盒子里，

“P值为零”，

一个声音传来，

“但你已经不能再拒绝，因为，P值已经死了”

从此，这个世界上充斥着谎言。

一、一个悲伤的故事：破灭的年少成名之梦

首先跟大家说一个悲伤的故事，该故事来源于nature最近发布的一篇文章“statistical errors”，我把这个故事叫做“破灭的年少成名之梦”

话说，弗吉尼亚大学有一位意气风发俊朗不凡的博士研究生莫德尔。

他做了一项关于关于政治极端分子的行为研究，样本大约有2000个人群，结果发现，相比较政治极端分子，政治温和派似乎更能辨别不同色度的灰色。

莫德尔对这项发现非常得意，因为数据也给出了非常积极的结果，统计结果显示P值为0.01，这意味着结果“非常显著”。莫老兄十分有把握能把自己的论文发表在高影响因子的刊物上。

由于担心实验结果陷入再现性争论，莫兄和他的导师决定重复实验，但是，在添加了新的数据之后，P值变成了0.59，这连0.05的显著性水平都没有达到！

伤心绝望的莫老兄知道，他观察的心理学效应站不住脚了，一同破灭的，还有那颗年少成名的美丽梦想。

实际上，问题并不在数据中，而是P值出了问题，正如罗斯福大学的经济学家史蒂芬所说，“P值没有起到人们期望的作用，因为它压根就不可能起到这个作用。”

为什么呢？为什么P值没有达到人们的期望？它的问题到底在哪？现在和数说君一起来梳理一下P值和假设检验的历史，并从中寻找答案吧。

二、P值和假设检验的历史

1. 拉普拉斯

P值得历史可以追溯到1770年，数学家拉普拉斯在处理50万左右的生育数据时，发现男性的生育率超过女性，对于这个无法解释的“超越”，他计算了一个叫做“P值”的东西，以确定这个“超越”是真实的（Stigler 1986, P.134）。

2. KarlPearson

很多统计学家误以为关于P值的正式文献是费雪发表的，其实不然，最早在文献中正式阐述P值及其计算的，是统计学家Karl Pearson，你可能不了解他，但是他的Pearson卡方检验你一定知道，这篇关于卡方检验的文章当时被发表在《哲学杂志》上，文章中一同被介绍的，还有一个被叫做“P值”的东东，见史料。

3. Fisher

P值能风靡学术界这么多年，费雪是第一推手，被他推动的除了P值，还有被称为“费雪学派”（Fisherian）的假设检验思想。简单介绍下他的思想：

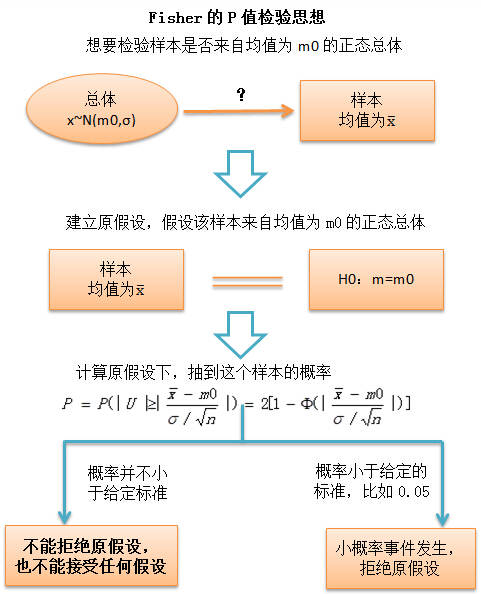
如果我们想要检验一个样本是否来自某个分布已知的总体，首先要建立一个“原假设”（null hypothesis），比如，下图的例子我们假设该样本来自正态总体N(m0,σ)，那么原假设为：

H0：m=m0

但实际上我们得到的样本均值不是m0，而是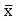，那么Fisher他老人家当时的想法是：在一个样本均值为m0的正态总体中，抽样得到这个均值为的样本的几率会有多大？我要是能计算出这个概率，就知道“这个样本来自该总体”这件事有多靠谱了，如果概率太小，就认为是不靠谱的事情，那么就可以认定这个假设是错的。这就是假设检验里的“小概率事件原理”，这个概率就是后来风靡学术界的“P值”，一般认为概率小于5%，就是不靠谱的事情，则需要拒绝原假设。

到此为止，Fisher大神只字未提“备择假设”，也从没说任何关于“接受”某个假设的事情，在Fisher的检验哲学里，

检验是基于无限总体中抽出的一个（注意是一个）样本；
显著性检验的基础是基于原假设而得出的假想概率，这些检验不能导出任何关于真实世界的概率论断。

因此，费雪以及他的P值检验思想，从来没有涉及到“备择假设”的概念，没有被认为可以用来证明某个假设是对的。

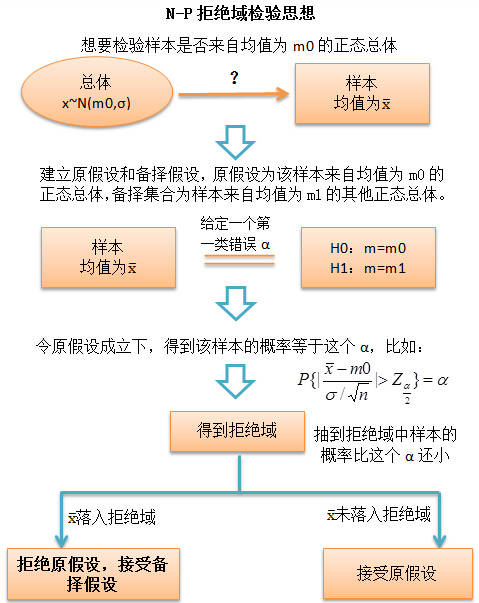
4. Neyman-Pearson

后来流行的“备择假设”的概念是在另一个重要的检验思想里提出的，即Neyman-Pearson（以下简称N-P）检验思想。N-P学派发源于费雪的思想，但却与之不太一样，他们两派相互争论了很多年。相比较于Fisher学派，Neyman他们主要有三个不同：

（1）引入备择假设

Neyman本人曾说，“接受一个假设H，仅仅意味着采用决策A要比决策B好，并不能说明我们必须要相信假设H就是对的。”

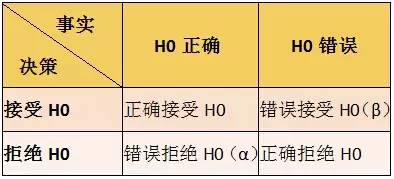
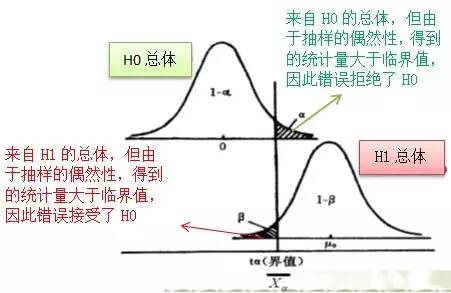
（2）引入两种错误：第一类错误和第二类错误

第一类错误是指拒绝了一个正确的原假设（α），第二类错误是指接受了一个错误的原假设（β）；

Power=1-β,被称为检验效力，它代表着拒绝一个错误假设的概率；

N-P的检验思想是，控制第一类错误（一般事先给定），使得第二类错误的值越小越好，即power越大越好。

（3）使用拒绝域来进行检验

在N-P的思想框中，完全没有提到P值，他们使用拒绝域来对假设进行判别，具体检验思想见下图：

（4）错误的混合

比较以上两个检验我们发现，Fisherian和N-P的检验思想完全不同，

费雪学派的P值检验思想，没有涉及备择假设，也从来没有被严格证明可以用来证明某个假设是对的。实际上，当我们抽取的样本变化时，得到的P值也会变化，结论也会随之变化。
N-P学派使用备择假设，在判定是接受还是拒绝某个假设的时，同时会给出两类错误以及power作为辅助参考，但是该学派（包括Neyman本人）从来不承认“P值”这个东西。虽然样本不同，他们的结论也会不同，但是N-P方法会在每个结论的后面给出相应的power，说明该结论的靠谱程度，相对于P值检验，这个方法更加规则严密。
Fisher和Neyman两人知道对方的观点，但是彼此都不能相容，Neyman批评Fisher的某些工作从数学上讲比“毫无用处”还糟，Fisher对Neyman方法给出的评价是“无比幼稚”、“在西方学界中简直骇人听闻”（Nuzzo,2014）。

然而后世的许多统计学家错误的将两个方法进行了混合，衍生出这样的判别标准，即:

用p<α作为判断标准，以决定接受原假设还是备择假设

如Gibbons（1986，p.367）说：“P值与古典方法（即Neyman-Pearson）的关系是，如果p<=α，我们就要拒绝H0，如果p>α，我们就要接受H0。”

三、悲剧的结论

梳理完P值和假设检验的历史，你应该知道为什么罗斯福大学的经济学家史蒂芬说，“P值没有起到人们期望的作用，因为它压根就不可能起到这个作用。”了，因为P值从来没有被证明可以用来接受某个假设，即使是拒绝假设，也是基于某个样本得出的结论，当样本变动时，结论很可能也会变动。

P值检验会如此不靠谱？其实，Fisher本人对统计检验的观点更加悲观，他认为，统计学的功能仅仅在于归纳推论（inductive inference），而不是归纳行动（inductive behavior）；统计检验应该止于归纳结论，而不涉足于行动判断（Lv,2012）。

这是一个悲剧的结论，不仅对梦碎的莫德尔老兄，也对所有运用统计学的研究者。

四、解决之道

面对“P值至上”的种种恶果，统计学家们给出了其他的解决方法，

避免使用“显著”或“不显著”来进行判断。如心理学家Cumming建议，研究者应当给出置信区间和power，以让读者明白研究结果的靠谱程度。
使用贝叶斯等决策方法。下图是贝叶斯的判断准则，没有P值的参与。

对同一个数据使用多种方法进行分析。结果越是不同，就越有可能出现重大的发现。

数说君曰：P值死了，这是统计学的重生

参考文献：

Fisher, R.A. (1925), StatisticalMethods for Research Workers, Edinburgh: Oliver and Boyd.

(1929), “The Statistical Method inPsychical Research,” Proceedings of the Society for Psychical Research, London,39, 189-192.

(1935b), “The Logic of InductiveInference,” Journal of the Royal Statistical Society, 98, 39-54.

(1935c), “Statistical Tests,”Nature, 136, 474.

(1945), “The Logical Inversion ofthe Notion of the Random Variable,” SankhyN, 7, 129-132.

(1960),“Scientific Thought and the Refinement of Human Reasoning,” Journal of theOperations Research Society of Japan, 3, 1-10.

(1966), TheDesign of Experiments (8th ed.), Edinburgh: Oliver and Boyd

Gibbons,J.D. (1986), “P-Values,” in Encyclopedia of Statistical Sciences, eds. S. Kotzand N.L. Johnson, New York: Wiley, 366–368.

Neyman, J. (1950), First Course inProbability and Statistics, New York: Holt.

(1967), “R.A. Fisher (1890–1962), AnAppreciation,” Science, 156, 1456-1460.

Pearson, E.S. (1928a), “On the Use and Interpretation of CertainTest Criteria for Purposes of Statistical Inference. Part I,” Biometrika, 20A,175-240.

(1928b), “On the Use and Interpretationof Certain Test Criteria for Purposes of Statistical Inference. Part II,”Biometrika, 20A, 263-294.

(1933), “On theProblem of the Most Efficient Tests of Statistical Hypotheses,” PhilosophicalTransactions of the Royal Society of London, Ser. A, 231, 289-337.

ReginaNuzzo, “STATISTICAL ERRORS”, nature

陈希孺.（2002）.数理统计简史. 长沙：湖南教育出版社

吕小康.（2012）.Fisher与Neyman-Pearson的分歧与心理统计中的假设检验争议.心理科学

相关内容

假设检验

关注 8

假设检验是推论统计中用于检验统计假设的一种方法。而“统计假设”是可通过观察一组随机变量的模型进行检验的科学假说。一旦能估计未知参数，就会希望根据结果对未知的真正参数值做出适当的推论。统计上对参数的假设，就是对一个或多个参数的论述。而其中欲检验其正确性的为零假设（null hypothesis），零假设通常由研究者决定，反映研究者对未知参数的看法。相对于零假设的其他有关参数之论述是备择假设（alternative hypothesis），它通常反应了执行检定的研究者对参数可能数值的另一种（对立的）看法（换句话说，备择假设通常才是研究者最想知道的）。假设检验的种类包括：t检验，Z检验，卡方检验，F检验等等。