你真的会用 t-SNE 么？有关 t-SNE 的小技巧

2018 年 5 月 28 日 专知

【导读】t-SNE[1] 是高维数据可视化的一个重要工具，但是在真实的使用场景中，t-SNE 的表现，总是令人很困惑。有人说： t-SNE有一个叫困惑度(Perplexity)的参数，貌似越高，结果越令人困惑。本文将跟读者一起，探索t-SNE 的各种表现，从而有效的利用它。

t-SNE 是 2008年L.v.d. Maaten和G. Hinton(没错，又是他) 在 JMLR期刊的一篇论文《Visualizing data using t-SNE》中提出的，感兴趣的读者可以在文末找到下载链接。到今天t-SNE 已经成为机器学习领域的基础工具之一。它可以将数百上千维的数据降维打击到人能够解读的维度(1,2,3维)。然而，笔者总能看到人们在对 t-SNE生成的图像的解读上出现各种问题，因此也有了本文。

t-SNE 的目标是，将一组高维空间里的点，映射到低维空间(为了方便讨论，本文默认为2维)，然后能够在一定程度上保持这些点在高维空间内的关系。 这个算法是非线性的(所以不是投影！)，而且，在不同的数据区域，运用的变换方式不一样(这是大家对 t-SNE 误读的主要原因)。

t-SNE有一个参数叫：perplexity，困惑度。其实perplexity可以理解为是一个用来平衡 t-SNE 关注局部变换还是关注全局变换的权重。也可以理解为，perplexity 是刻画每一个点的邻接点的个数的参数。它对 t-SNE 的结果的影响很细致，以至于改变了 perplexity(困惑度), t-SNE 的结果的变换让人摸不着头脑，有人说，困惑度的值越高，越令人困惑，甚至有怀疑，这个超参没啥用。特别是，t-SNE算法，同一个数据运行多次，结果是总会有一些变化，也即，对于稳定的输入，它有时候能产生稳定的输出，有时候又不能，这就让人更困惑了。

为了充分的了解高维数据的各种特征，我们需要花式调节t-SNE 的超参，期望能够从 t-SNE给出的结果中，看出高维数据的一些特征。

1. 多调超参，多些观察

很多读者问， t-SNE 的超参到底有啥用？在本文，作者就简单的控制变量了一下，来理解超参的作用。 t-SNE 的超参有三个：perplexity(困惑度)，step(迭代次数)，epsilon(学习率)。我们首先来看 perplexity。

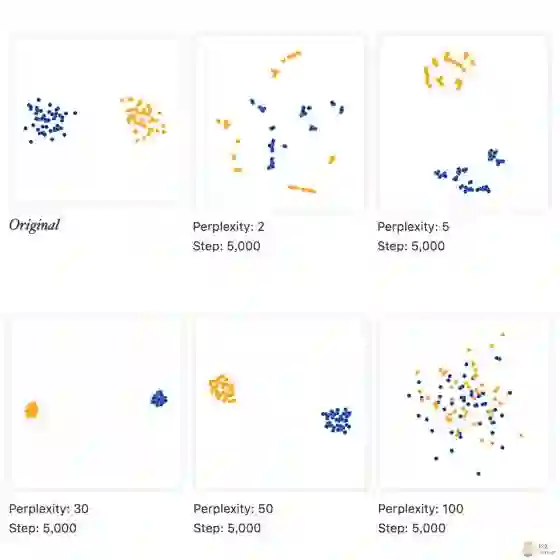
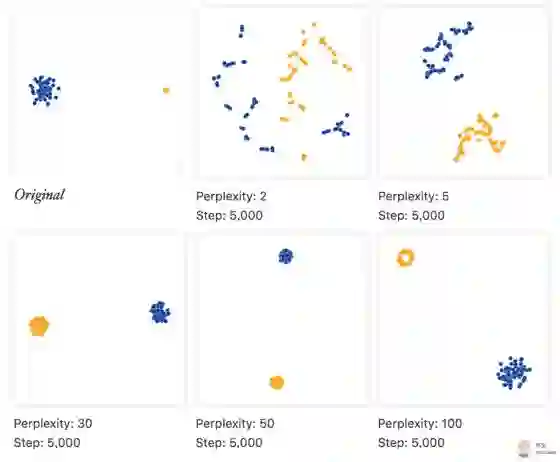
我们生成了高斯模型生成了两簇节点, 每簇50个，用蓝色和橙色表示，作为 t-SNE 的输入。然后，将perplexity 设成， 在提出t-SNE的 paper中，作者建议的范围是。 step 为5000， epsilon 为10:

简单观察，可以发现，更小的 perplexity，更关注局部的链接， 而跟原始节点数差不多的 perplexity，能够变现出很好的效果 ，过于大的perplexity，整个图就变得非常奇怪。

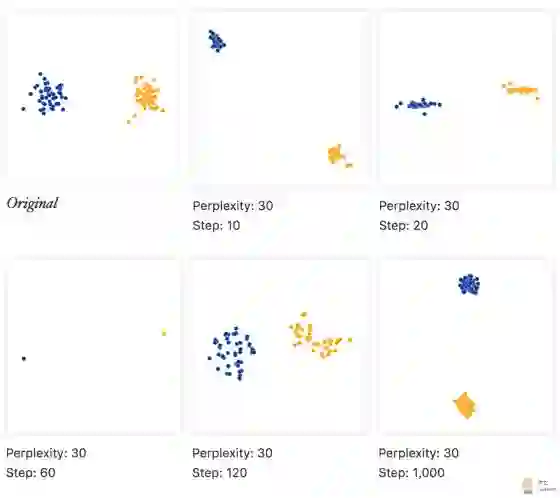
如果固定 perplexity，考虑不同的 step, 产生的效果如下：

上面的图片显示了5种不同的 step的取值。在10,20,60步的图，很像是一维的情况，他们可以用一个直线连接。

无论是10， 20， 60， 120 它们都没有收敛。对于收敛，显然不同的数据集需要不同数量的迭代。

2. 相同的超参，同一个数据集，多次运行，会得到同一个图像么？看情况！

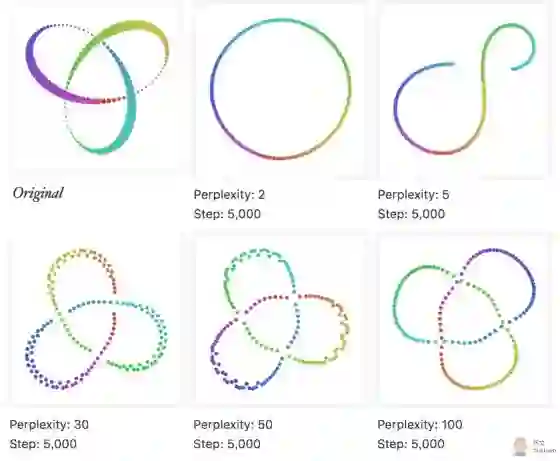
考虑一组典型的环装结构：

在不同的perplexity的情况下， t-SNE 给出的形状非常不同。而，跟原始数据节点差不多的perplexity 更能体现原始数据的信息。

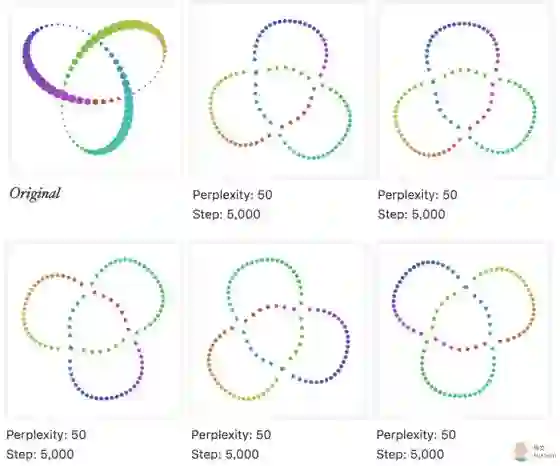
那么，相同的超参，多次运行，会得到同样的结果么？

在perplexity为2时，每次运行，都有新的结果产生。

在 perplexity 为50时，多次运行的节点，虽然图像不同，但是蕴含的信息是相似的。

显然，如果你的数据，在给定超参下多次运行，每次都有新体验，很可能是你的 perplexity还需要再调一调。

3. 原始数据的簇的大小能通过 t-SNE 的结果看出来么？不好意思，不能！

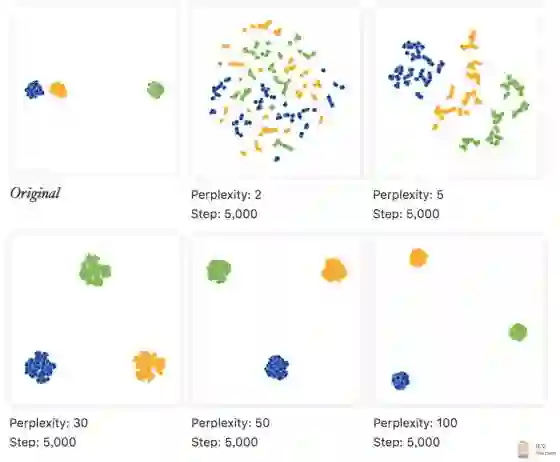
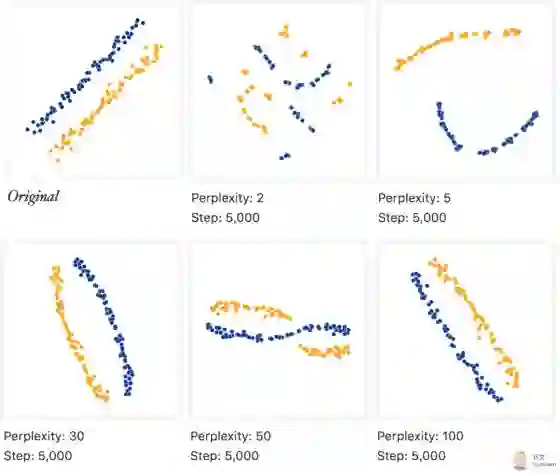
在第一个例子中，我们用高斯模型生成了两簇节点，每簇50个节点，如果这两类高斯模型的协方差矩阵不一样呢？我指的是，节点数量不变，簇的大小变化。我们生成了两个簇，他们的方差差异非常大，然后固定 step为5000，调整 perplexity。

正如左上方的原始图所示，蓝色和橙色的簇，方差差异非常大。然而，从t-SNE 的结果结果来看，反而两个簇差不太多，特别是在 perplexity为5， 30， 50的时候，它们几乎一样的。这是因为， t-SNE 算法，将它的结果图中的距离，跟簇内的密度相适应，导致紧密的簇被放大，而稀疏的簇被缩小。t-SNE 是非线性的，在这一点的表现上，它跟普通的高维空间的点在低维空间的线性投影区别很大。

另外，同样是 perplexity 为100， step 为5000，本例的结果与第1节：超参到底有什么用？中的例子有显著的不同，而它们原始数据的区别，仅仅是一个方差大了些。

4. 原始数据的簇之间的距离能通过 t-SNE 的结果看出来么？不好意思，不能！

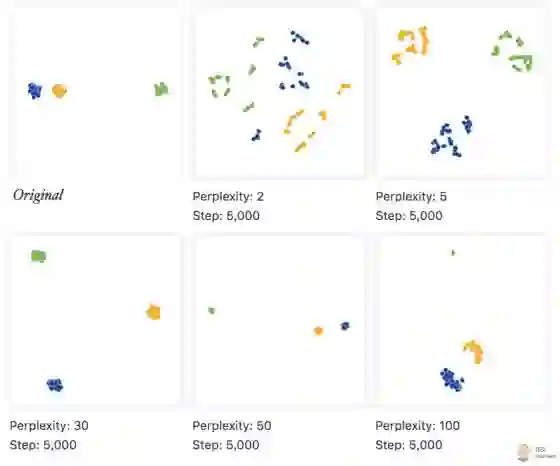
那么，原始数据的簇之间的距离对 t-SNE 的结果有影响么？我们生成了3个簇，其中，蓝色和橙色两类里的比较近，而绿色的则较远，然后，我们调整 perplexity，来查看结果。

我们看到，当 perplexity 取值在的时候，根本看不出差距。而当 perplexity 设置成时，还是能看出点什么的，那么确实是么？

当我们把每一簇的点的个数从50提升到200，距离不变。那么，无论 perplexity怎么取值都没能表示出原始数据的之间的距离。

原始数据，可能有多种不同量级的簇，而且它们之间的距离也不同，然而，一个固定的perplexity 很那同时覆盖到所有的簇的大小和位置，然而， perplexity 是一个全局参数，这就非常尴尬了。

5. 随机噪声，一点也不随机

令人最尴尬的事情，莫过于把硬生生把随机数据，解读出各种特征。

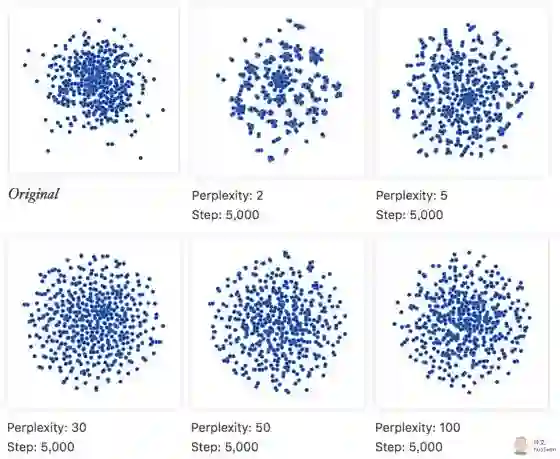
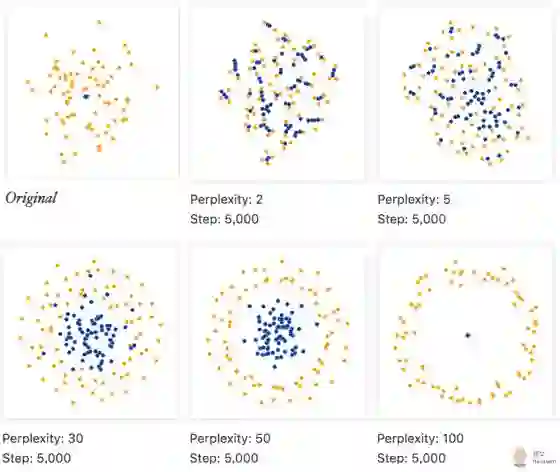
在本例中，我们从一个100维的单位高斯模型中，随机采样500个点，左上角的原始图，是这500个点的前2维。我们将这500个100维的高斯噪声，丢给 t-SNE。如果不告诉你，原始数据是随机的，随着你调整 perplexity，你可能以为你找到了原始数据的分布结构：均匀分布。。。

6. 原始数据的形状能从 t-SNE 的结果中看出来么？可以！

我们生成了两簇条状数据，每簇75个节点，然后将他们输入到 t-SNE 中：

通过不断的调试perplexity，我们可以解读出，原始数据是具条带状的。

7. 原始数据的拓扑结构能从 t-SNE的结果中看出来么？可以！

最简单的拓扑关系就是包含。我们从两个50维中高斯中，生成了两簇节点，每簇75个，但是蓝色的簇比橙色的簇更紧密。且蓝色的簇被橙色的簇包含。从 perplexity等于30开始，我们就能从 t-SNE 的结果中看到明显的拓扑结构了，这里，我们又能看到 t-SNE 的神奇作用：紧密的簇被放大，稀疏的簇被缩小。

引用：

•paper： Visualizing data using t-SNE [PDF] L.v.d. Maaten, G. Hinton. Journal of Machine Learning Research, Vol 9(Nov), pp. 2579—2605. 2008.

原文发布在https://distill.pub/2016/misread-tsne/，由专知团队翻译成中文，重新组织，配图。

更多专业AI教程资料请加入专知人工智能知识星球群获取，扫描下面二维码即可！

-END-

专 · 知

人工智能领域主题知识资料查看与加入专知人工智能知识星球服务群：

【专知AI服务计划】专知AI知识技术服务会员群加入与人工智能领域26个主题知识资料全集获取。欢迎微信扫一扫加入专知人工智能知识星球群，获取专业知识教程视频资料和与专家交流咨询！