【CAA智库】复旦大学张军平:爱犯错的智能体 – 视觉篇(十):自举的视觉与智能

一个鼻子又高又长的小个子干瘦老头,倚着一块石头坐着。他眼睛看着欢腾跳动的火舌,讲起了人们从来没有听到过的奇妙故事。听他讲故事的人,不时笑得前仰后合。
“敏豪生,可真行啊,奇事都让你遇上了!”
但是敏豪生不在乎大家信不信他讲的,等笑声一停,他又接着讲下去。。。
图1敏豪生抓着自己的头发把马和自己从泥沼里拔出来
抓着自己的头发从泥沼里拔出来
一次,我们受到凶猛追击。我决定骑马穿过沼泽地。然而,我的马匹跑得太累了,本来可以跳过沼泽泥淖的,这会儿却没能跳过去,噗的一声落入泥淖中,陷在里头,动弹不得了。
身下的马带着我往下沉。我那匹马的肚皮已经陷在污泥里了。不能指望谁来拉我们出去。泥淖把我们越来越深地往下吸、往下拉。危险极了,可怕极了。眼看马整个儿陷进了险恶的泥淖,很快,我的头也开始埋进沼泽的污泥之中。只有我的这顶军官帽还露在泥淖上面。
看来我们是没救了,我们必死无疑。还好,我急中生智,一下想起我的双手有惊人的力量。我一把抓起我自己的头发,用尽全身的力气把自己往上拽。我毫不费力地把自己从泥淖中拔了出来,而且顺带还把我的马也往上拽。我的双腿铁钩一般的强有力,把马肚拨了出来。
这可不是如你们所想象的那样,是一件轻而易举的事哟!要不信,你们倒是自个儿试试,看能不能抓住自己的头发一下就把自己提向空中。
----摘自《敏豪生奇遇记》
《敏豪生奇游记》原为德国民间故事,又名《吹牛大王历险记》,后由德国埃•拉斯伯和戈•毕尔格两位作家再创作而成。这则故事传递了一个概念,叫“自举”,能找到的对应英文名是“Bootstrap”,意思是“to pull oneself up by one’s bootstrap”,白话就是“拨鞋法”。在这个故事里,敏豪通过“自举”逃出了沼泽,安全地进入了下一个吹牛环节。看似挺荒谬的情节,那在智能体和人工智能领域有没有类似的存在呢?
要用到自举,无非是自身的能力受限,才得想办法扩展。人的视觉就是如此,在很多方面不是那么尽如人意的。它不如鹰的眼睛那么敏锐、能在运动状态下从10公里的高空及时发现草丛里的猎物,也不如蜜蜂能区分紫外线波段白色花的差异,也不能像响尾蛇一样感受红外端的热能。
不过人也有一些奇特的感知能力,比如传说中的“第三只眼”、“背后的眼睛”,有科学家将其称为盲视,即身体上的其它感观系统感受到了周边潜在的变化,却没有经过视皮层的脑区进行加工产生的下意识反应,但人会“以为”自己看到了。尤其是女性,可能冷不盯会觉得背后有人在看她,而且经常发现感觉是对的,这说不定就与“盲视”有关。世界著名的漫画书《丁丁历险记》之《蓝莲花》也描绘过这种“盲视”的情形,见图1。当然,这些“盲视”的情况也可能是心理作用引起的,目前并无定论。
图2 杜邦、杜帮和丁丁在1937年左右的上海街头(取自《丁丁历险记》之《蓝莲花》)
不管是否有神奇能力,人的视觉有很多不足。在光的强度上只能感受10的2次方的变化,而自然界的光强是从10的负4次方到10的6次方,近10的10次方量级的变化。于是,人的视觉多了个“亮度自适应”的自举功能。这是人最常用的能力。比如走进电影院时,开始一片漆黑,过了一段时间,人的眼睛逐渐适应了,便能看清楚周边的环境了。更严格地话,这一能力可用图3来说明。
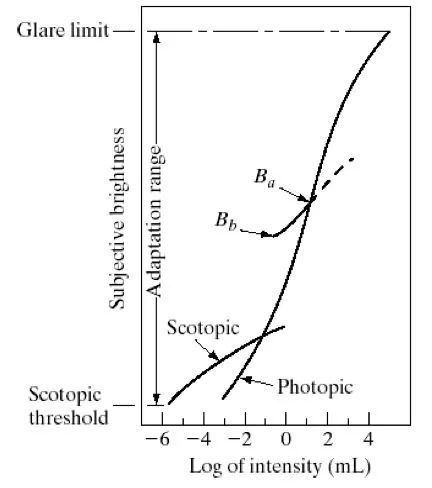
图3亮度自适应:白昼视觉与夜视觉[1]。横坐标:光强的对数;纵坐标:主观亮度
图中横坐标是光强的对数,即10个数量级;纵坐标反应了人眼的适应能力以及主观感受的亮度变化。白昼视觉(Photopic)的感光范围从10的负2次方到10的4次方,夜昼视觉从10的负6次方到10的0次方。人的视觉可在给定Ba的强度值时,在Bb的正负区间内形成感光,但可以根据Ba的变化来进行自适应。一旦到了夜视觉(Scotopic)区间时,视力会按夜视觉的曲线来感知环境。
人类亮度自适应的机理是什么呢?它和猫通过自动调节瞳孔的大小来适应不同的光照变化的机理不同,是通过后端的视神经元的分工协作来实现的。白昼视觉主要由光线落在视网膜焦点、即中央凹处的视锥细胞完成,夜视觉则由主要分布在中央凹以外的视杆细胞来实现。
别小看这点自适应,现在的图像处理在处理光强差异大的场景时仍然是一筹莫展。比如白天,各位不妨拿手机从室内拍下室外的场景,看看是否能保证室内室外都能成像清晰,明暗分明?再比如,在地下停车场的外面,摄像头是否能把停车场里外都同时监测?
当然,这种自适应有时候也会带来风险。比如在晚上开车,突然对面过了一辆开着远光灯的车,那么驾驶员在视觉上会直接被误导到白昼视觉,而无法看清黑暗环境里的人或其他目标。这种“瞬间致盲”极易导致交通意外的发生。
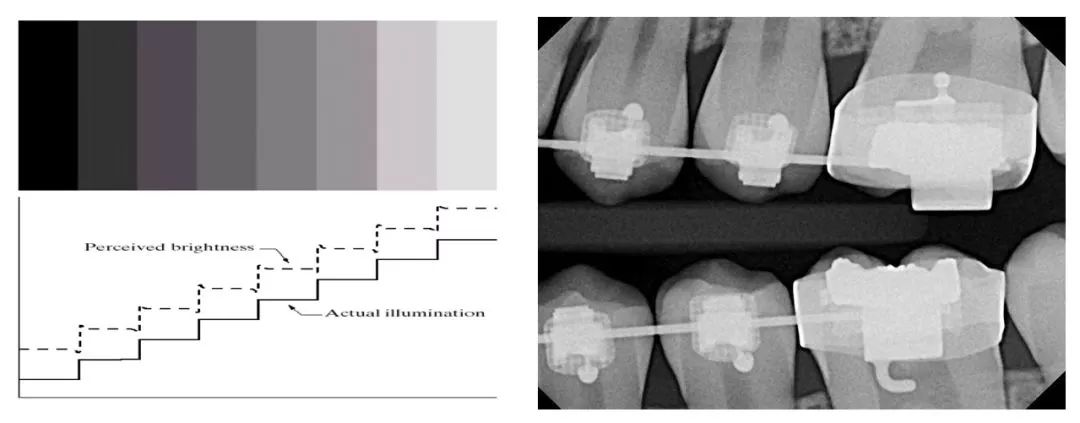
除此以外,人的视觉对边缘的反应也有自举的表现。图4左图是一组光的强度按宽度逐渐变化构成的。将其强度的柱状图画出来,就象一组台阶。然而,有实验表明,人在感知时,会在两个相邻的强度级的连接处产生“感受到”的向上和向下的强度变化,称之为“马赫效应”,可以称其为伪边缘。这种伪边缘的出现,可拉开相邻目标或前景、背景之间的差异,使轮廓会变得更清晰,继而能帮助人类更好地区分目标和背景或其他目标。
图4左图:马赫效应[1];右图:牙齿X光片(网图)
然而,马赫效应形成的伪边缘有时候也能产生错觉。比如这张戴着牙套的牙齿X光片,如果不熟悉牙齿的基本构造,一个刚上岗的X片读片员很容易以为这些牙齿都出现了断裂,因为每颗牙齿上都有两种不同的灰度。而这种断裂就是马赫效应形成的错觉。其真正的原因是牙齿包含牙釉质和牙本质,两者的密度不同,因而X光通过后,会在感光片上形成不同的光强值,相邻、有差异的光强值会诱导出伪边缘现象,导致经验不足的医生产生误判。
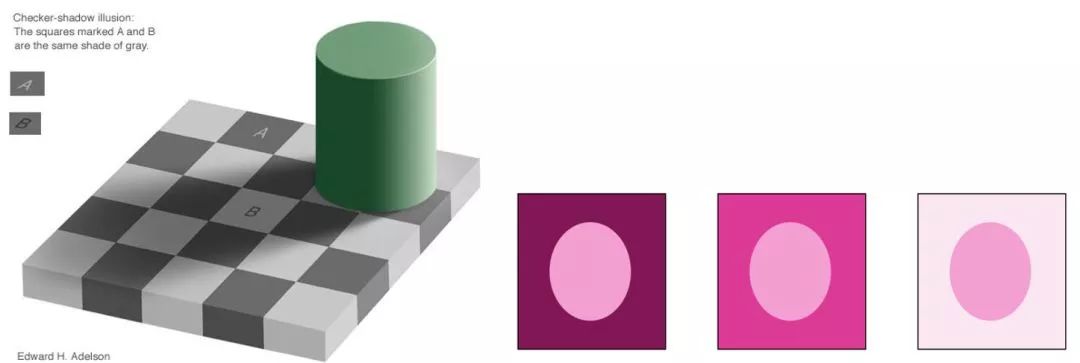
不仅相邻黑、白、灰度的差异会形成边缘错觉,相邻亮度、颜色的对比还会形成对亮度和色彩的判断错觉,如图5所示。图像处理领域将其称为“同时对比”现象,也有些领域将其称为“色彩错觉”。其原因在于人的视觉系统易受周围环境色彩的影响,在色彩对比因素存在的前提下,对关注的色彩或灰度产生深浅不一的错觉。从某种意义来讲,这种错觉可能为了提升人对所关注目标的显著程度而形成的。不过,负面效果就是不容易形成统一的色视觉判定结论,因为人的色彩视觉是主观而非客观的,比如图6中的衣服颜色就曾经引起过很多人的讨论。
图5同时对比现象:左:灰度图的同时对比;右:彩色图的同时对比
图6衣服是什么条纹的?黑蓝、黄白还是其他?
人类的视觉系统能通过自举来提高感知外部世界的能力,那么人工智能中有没有类似的机制呢?
从现有的理论体系来看,在数据的分布存在自举式模拟,分布加权以及数据不足时也存在自举的办法,但这些都与视觉中的自举大相径庭。具体如下:
1、数据分布的自举
实现人工智能的一个必要步骤是学习,从数据中学习。但数据的分布是什么样的?并非一开始就明了。所以,一般会假设数据服从某个分布。比如像许愿池中扔的硬币一样,如图7,中间密周边逐渐稀少,这就是传说中的、人工智能领域最常用的高斯分布,因为他能极大方便后面的各种处理。
可是分布是多种多样的,也并非所有情况下,分布都能精确且事先知道。但做数据分析或设计人工智能算法时又需要有分布的形式,于是科学家们就设计了一种自举的技术去逼近真实的分布。粗略来说,就像玩扑克牌一样,每次抽玩牌再放回去。在给定了牌/数据的前提下,通过对牌/数据进行反复的抽样,每次都有放回的抽一组和原始牌/数据数量相同的数据,获得的数据集称为自举或再抽样样本集。
重复这一自举方式,通过分析其稳定性,就能比较好地逼近数据的真实分布。这是数据分布的自举,称为Bootstrap方法,最初由美国斯坦福大学统计学教授Efron在1977年提出,为小样本或小数据量来增广样本提供了好的办法。在此基础上,后来发展了大量的改进型“自举”方法,都是期望能更好地从局部推测总体的分布。
图7左:掷硬币掷出的高斯分布;右:《赌侠》剧照
2、基于数据分布加权的自举
另一个自举是针对分类任务的,比如识别张三和李四的人脸图像。传统的方法往往假定每张图像或数据在分布中是等权重的。这种假设的不足在于,不容易区分容易分错的数据。于是1995年Yoav Freund就提出了Boosting算法, 通过同时组合多个较弱分类能力的分类器来改进分类性能[2]。1996年在此基础上Freund和Schapire提出了当年红遍机器学习及相关领域的Adaboost算法[3,4]。基于多个弱分类器的集成,该算法实现了优异的预测性能。在此背后,一个最重要的原因就是他会根据每个弱分类器的预测情况,对容易分错的样本给予更高的权重,从而确保其在下一轮采样时更容易出现或被采集到,直到获得精确的预测结果。这个针对数据错分的自举,最终成为了机器学习最成功且实用的经典算法之一。至于其在分类能力上成功的机理,尽管机器学习的著名期刊JMLR(Journal of Machine Learning Research)曾有一批学者来进行多角度的分析,真实和公认的原因仍未知。但其受到了自举的启发是毋庸置疑的。
3、数据不足的对抗自举
近年来,为了能进一步提高深度网络的性能,Ian Goodfellow2014年提出了生成式对抗网络[5]。一经提出,很快就成为人工智能领域研究者的主要研发工具之一。如果仔细审视,可以发现,其通过网络内部对抗器和判别器的反复博弈生成大量“虚拟样本”的思路,也能视为是一种自举。
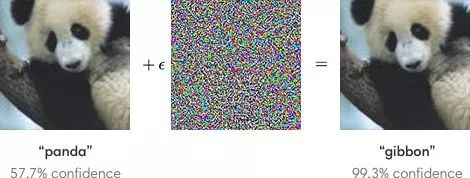
比较好玩的是,在取得异常好的性能的同时,这种自举式的网络和其他深度网络似乎都比较容易被攻击。据报道,对于图像识别任务,一两个像素的改变或引入随机噪声所构成的对抗样本就能导致网络产生错误识别,如图8。这多少有点像自举的视觉,会存在“同时对比”这种容易误导视觉判断的现象。毕竟没有什么系统可能是十全十美的,总会有例外。只是我们还不太清楚,这是否仅是稀少的例外,还是会变“黑天鹅”的意外。
图8易受攻击的深度网络:熊猫上叠加随机噪声,尽管视觉上仍能察觉是熊猫的图像,但深度网络却会高置信度地将其识别为长臂猿[6]
人工智能的终极目标是期望能模拟人类的智能,所以,自举的心智也是值得研究的,因为它意味着人能在受限的条件下极大地提高自身的能力。这有点像俗话所说的“走出自己的舒适圈”,也像90年代曾风靡内地的某培训学校的口号“挑战极限”。
关于这一点,20世纪初期哲学家怀海德曾在其1929年出版的、形而上学或“过程哲学”经典书籍《Process and Reality》(过程与实在)中指出, 人的认知、社会的认知最终可以上升到一种自我成长、自我成熟的阶段,正如宇宙和自然的演化,这可以视为更广义的自举。
而经济学家默顿·米勒提出的默顿定律(Merton Laws)认为,人最理想的状态是自我预言,自我实习。举个不恰当的例子,据说杨振宁约12岁时,就看爱物理书。有次他从艾迪顿的《神秘的宇宙》里读到了一些新的物理学现象与理论,便表现了极大的兴趣。回家后就跟父母开玩笑说,将来要拿诺贝尔奖。结果梦想真的实现了。这就是默顿定律的体现,是一种自我预言、自我激励、自我实现,也是一种自举的表现。
如果把自举的机制理解清楚了,尤其是视觉和心智方面的,也许我们就能找到构造自我发育、自我强化的人工智能体的办法了。
来源:CAA混合智能专委会
往期文章推荐

🔗【重要通知】中国自动化学会关于开展“2018-2020青年人才托举工程项目”推荐工作的通知
🔗【问卷调查】关于开展全国学会分支机构基本情况问卷调查的通知
🔗【通知】关于召开2018年“人工智能与智能制造”高峰论坛暨中国自动化学会华东六省一市学术年会的通知
🔗【CAC2018】2018中国自动化大会论文及注册相关问题答复(Q&A)
🔗【CAC 2018】2018年中国自动化大会“智能自动化新技术” 展览邀请函
🔗【2018重要学术会议指南】管理科学领域国内外重要学术会议推荐(10月-12月)
🔗【会员服务】中国自动化学会会员:现可免费申请IEEE Xplore数据库及InnovationQ Plus专利检索分析工具试用!