图如何双曲建模？弗吉尼亚理工Amazon最新WWW2022《双曲神经网络:理论、架构和应用》教程，附162页ppt

2022 年 4 月 27 日 专知

TheWebConf是中国计算机学会（CCF）推荐的A类国际学术会议，由国际万维网会议委员会（IW3C2）和主办地地方团队合作组织，每年召开一次，今年是第31届会议。本年度论文录用率为17.7%，TheWebConf即将召开，来自弗吉亚理工和亚马逊等学者的《双曲神经网络》教程，值得关注！

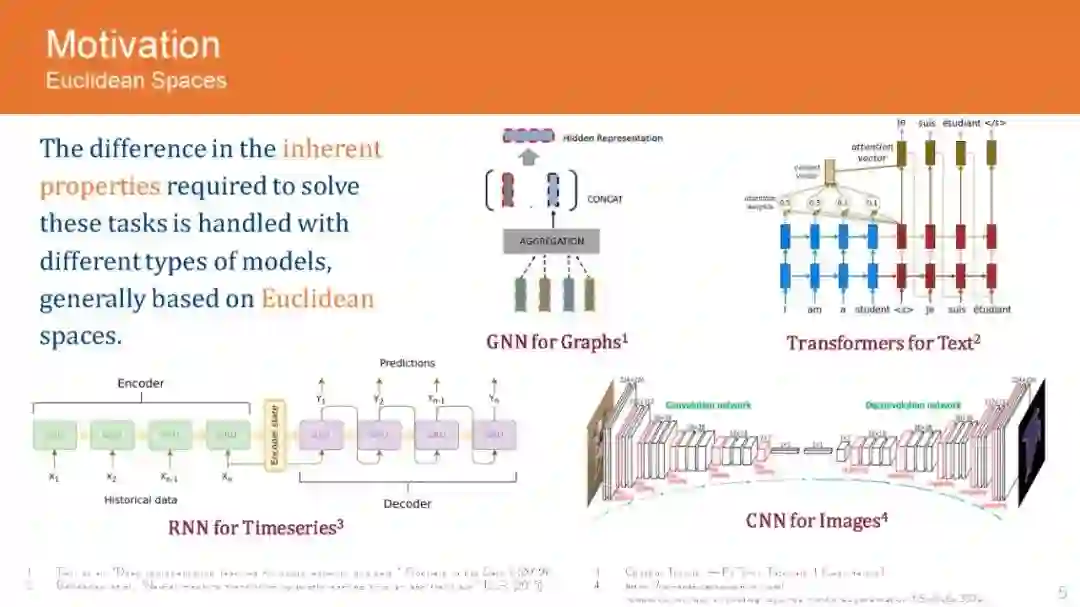
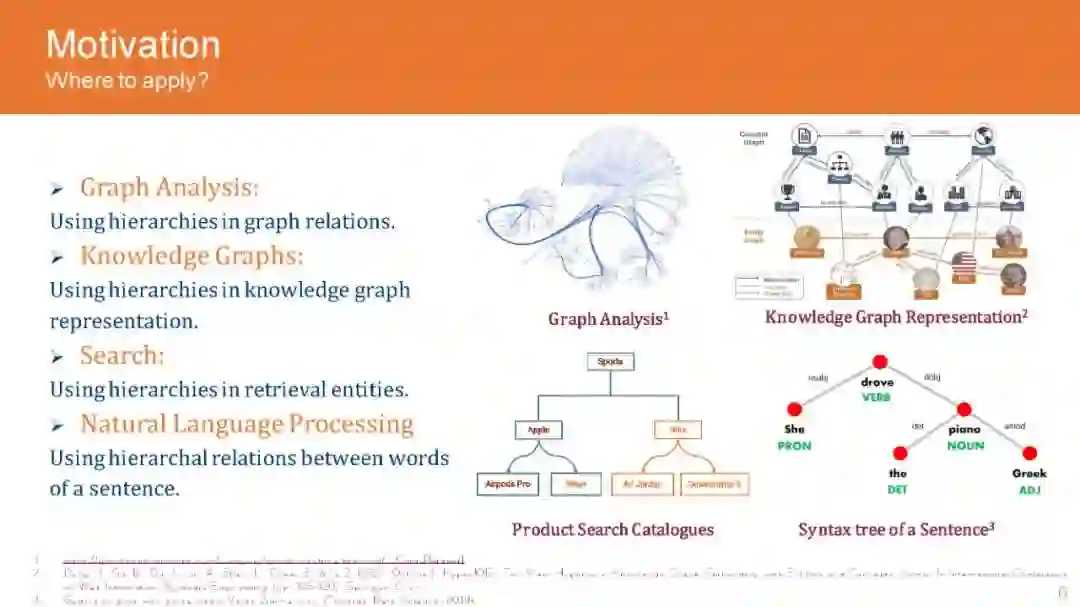
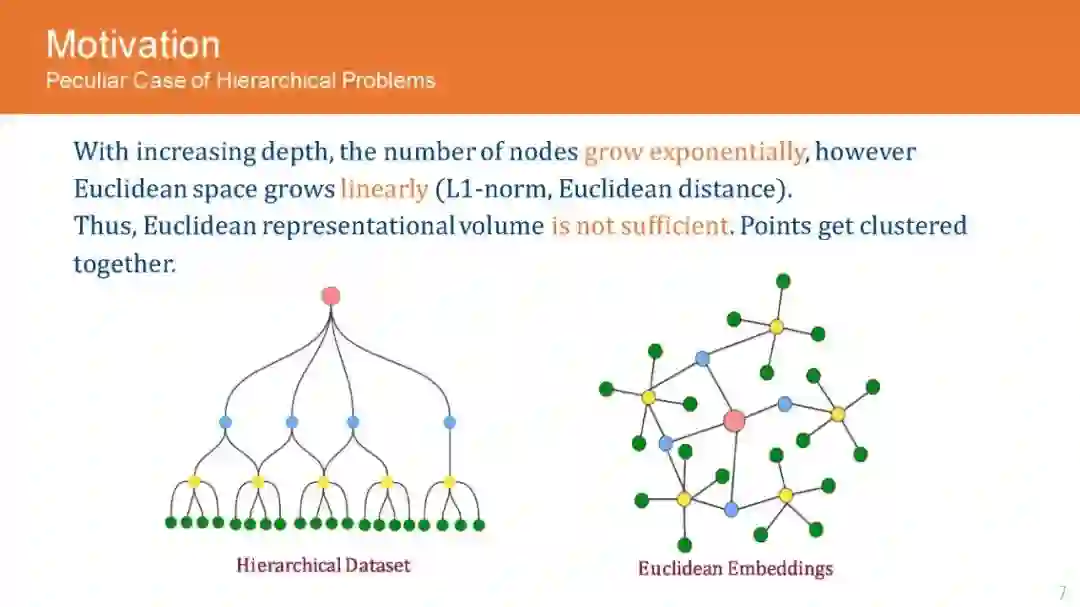
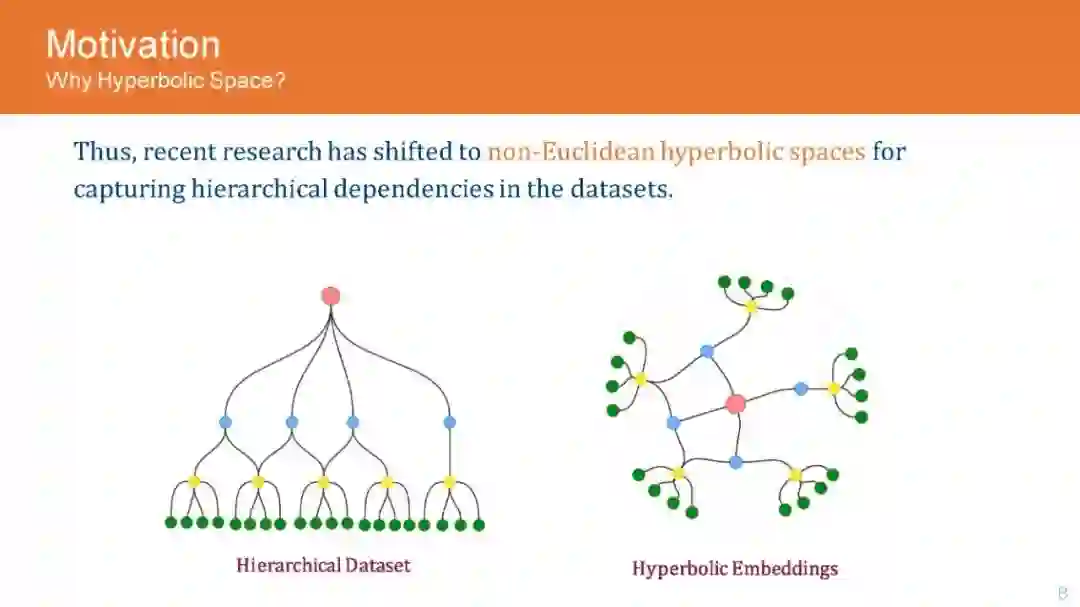
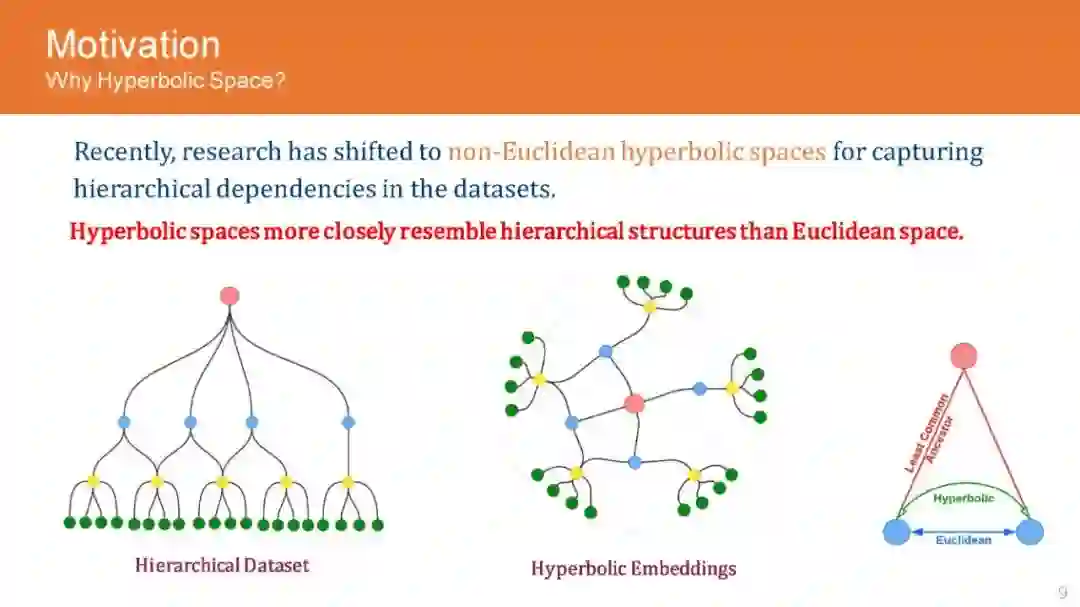
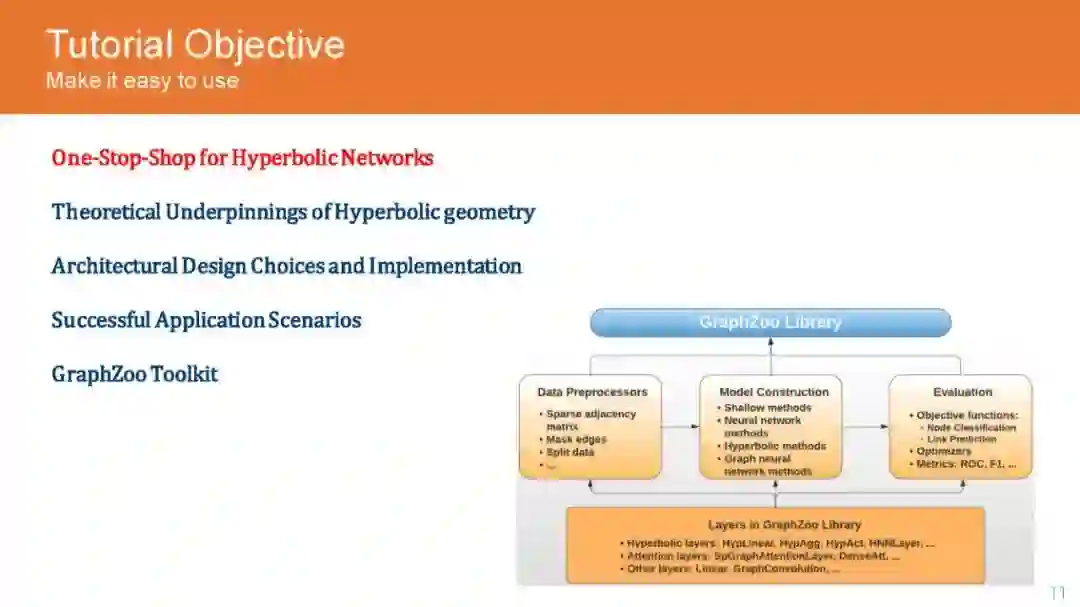
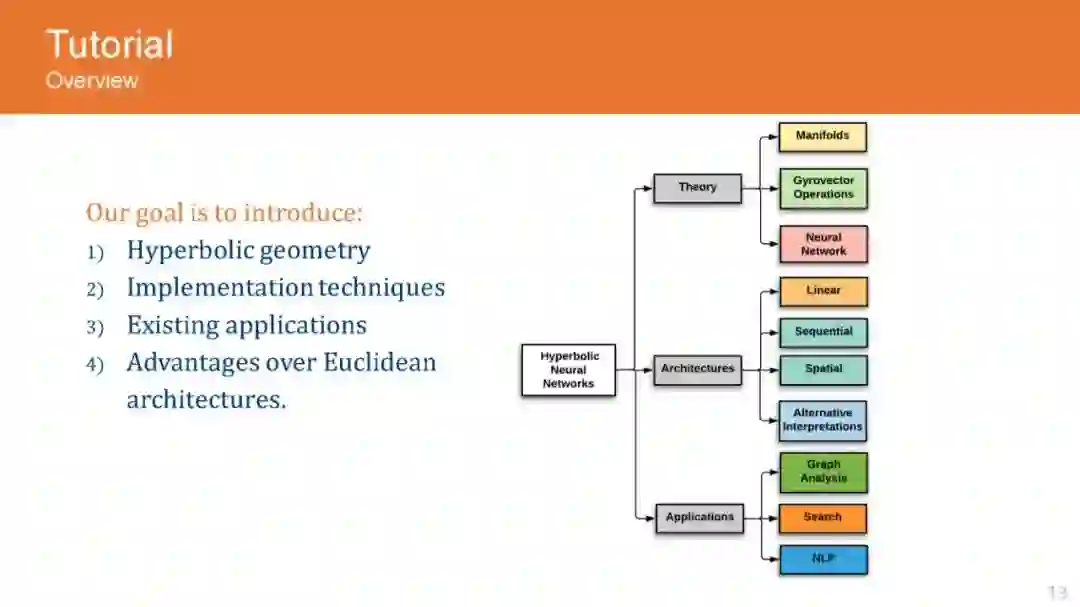
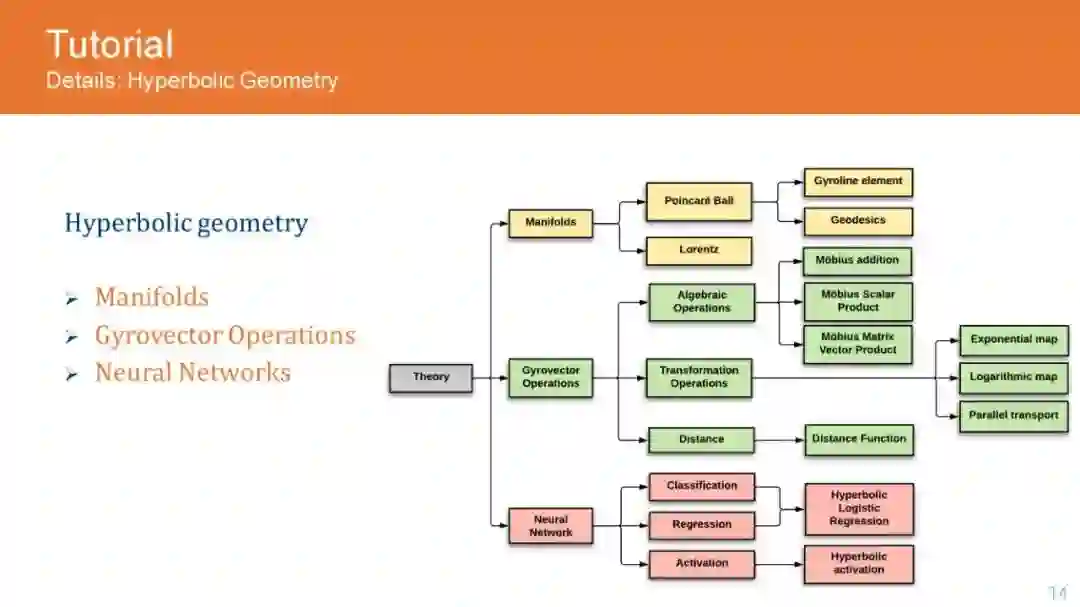
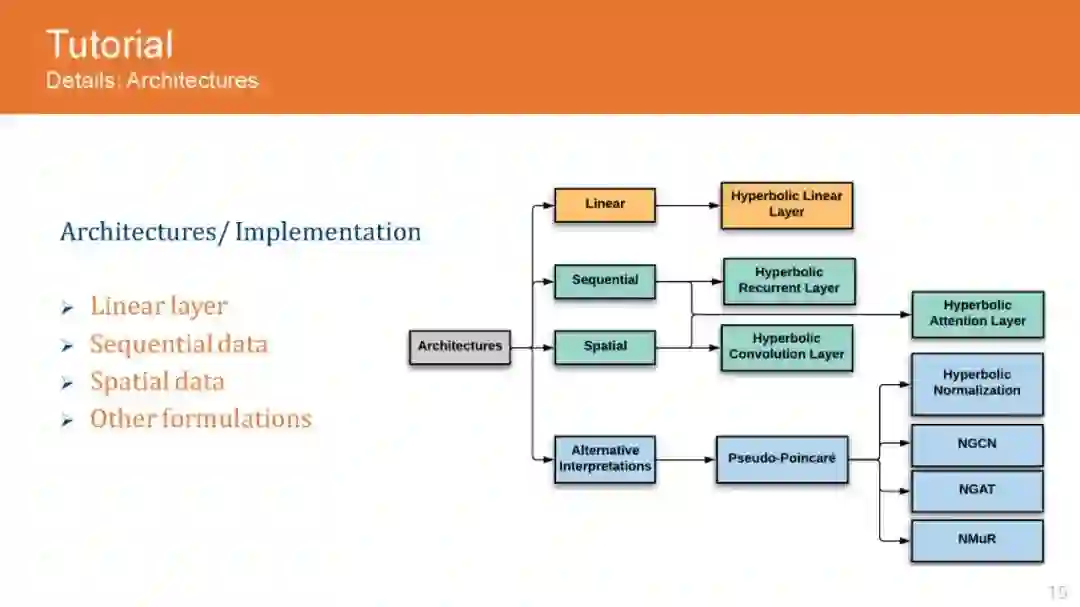
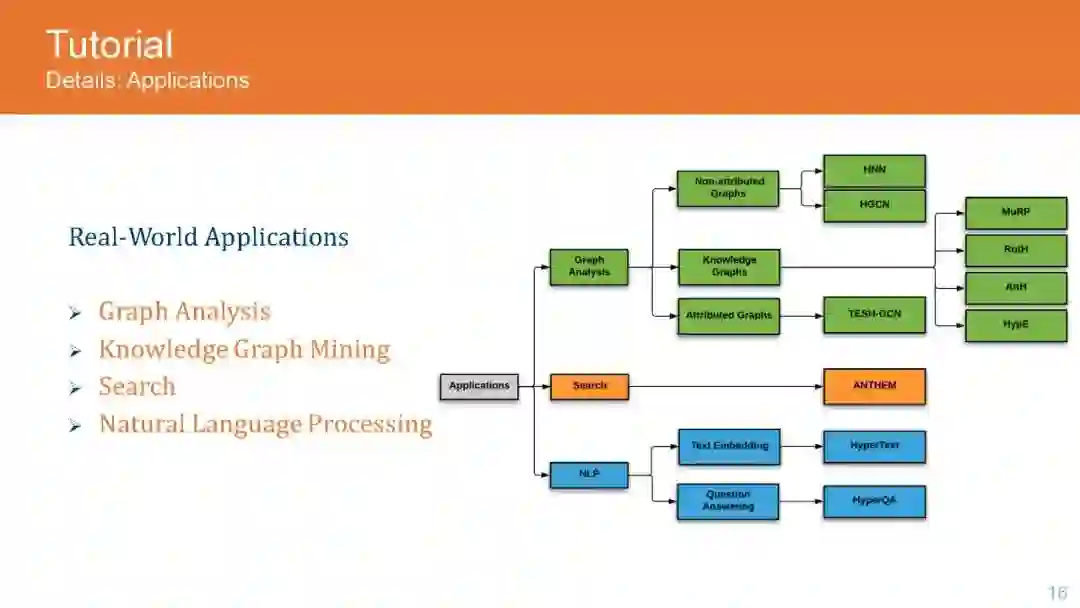
图是普遍存在的数据结构，广泛应用于许多数据存储场景，包括社交网络、推荐系统、知识图谱和电子商务。这导致了GNN架构的兴起，用于分析和编码来自图的信息，以便在下游任务中获得更好的性能。虽然图分析领域的初步研究是由神经结构驱动的，但最近的研究已经揭示了图数据集特有的重要属性，如层次结构和全局结构。这推动了对双曲空间的研究，因为它们能够有效地编码图数据集中存在的固有层次。随后，该研究也被应用到其他领域，如自然语言处理和计算机视觉，取得了令人惊叹的结果。然而，进一步发展的主要挑战是双曲网络的晦涩，以及更好地理解必要的代数操作，以扩大应用到不同的神经网络结构。在本教程中，我们的目标是向网络领域的研究人员和实践者介绍欧几里得运算的双曲等变，这是处理它们在神经网络架构中的应用所必需的。此外，我们描述了GNN架构的流行双曲线变体，如递归网络、卷积网络和注意力网络，并解释了它们的实现，而不是欧几里得网络。此外，我们还通过图分析、知识图谱推理、产品搜索、NLP和计算机视觉等领域的现有应用来激发我们的教程，并将性能提高与欧几里得的同类方法进行比较。

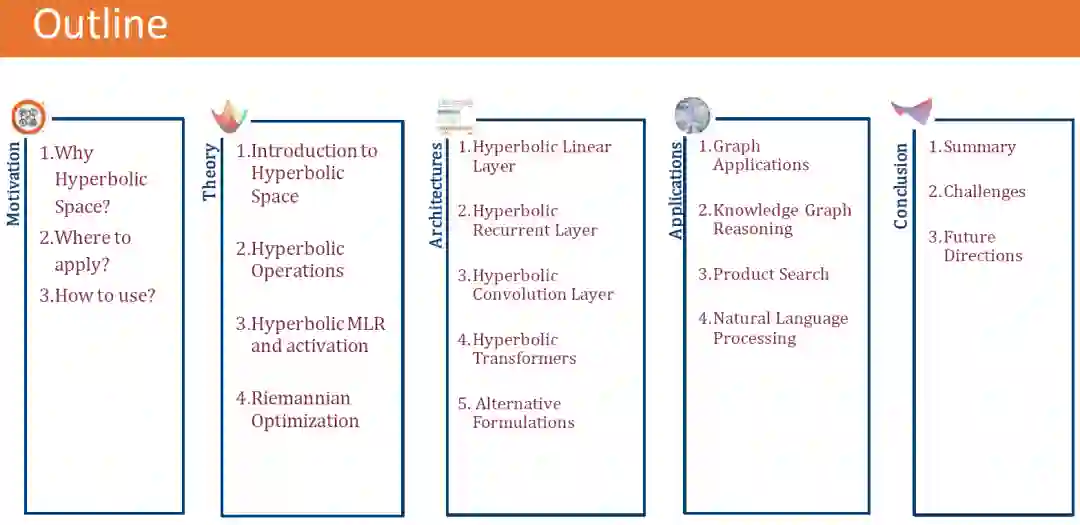
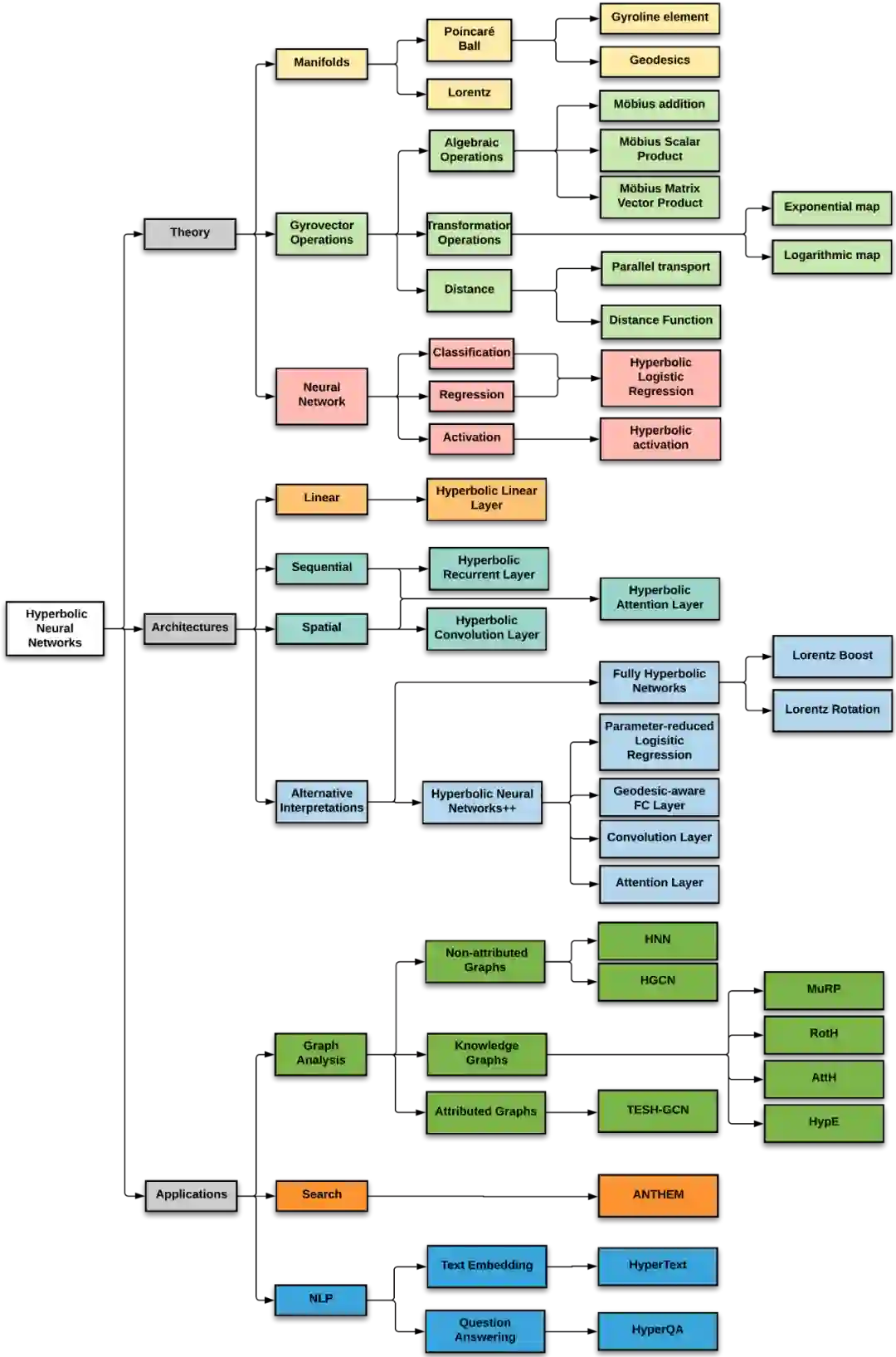
目录内容：

讲者：

Nurendra Choudhary是弗吉尼亚理工大学计算机科学系的博士生，在导师Chandan Reddy博士的指导下，他的研究重点是图分析和产品搜索领域的表示学习。他在WWW、NeurIPS、WSDM和COLING等顶级会议上发表相关论文。他获得了国际信息技术学院计算语言学硕士学位，期间他获得了2018年CICLING的最佳论文奖。

Nikhil Rao是亚马逊的一名高级科学家，他在那里从事大规模图建模和算法的研究，以改进亚马逊搜索。在加入亚马逊之前，他是帕洛阿尔托Technicolor AI Labs的研究员。Nikhil的研究兴趣和专长包括大规模优化、数据建模和挖掘，以及开发利用数据结构的算法。Nikhil在顶级会议和期刊上发表了几篇论文。他获得了来自UT Austin的ICES博士后奖学金和IEEE最佳学生论文奖。他拥有UW Madison的电气和计算机工程博士学位。

Karthik Subbian是亚马逊的首席科学家，拥有超过17年的行业经验。他领导着一个由科学家和工程师组成的团队来提高搜索质量和信任度。在来亚马逊之前，他曾是Facebook的一名研究科学家和负责人。在亚马逊，他领导了一个由科学家和工程师组成的团队，利用社交网络结构及其交互来探索信息传播和用户建模问题。此前，他在IBM T.J. Watson研究中心的商业分析和数学科学部门工作。他的专业领域包括机器学习、信息检索和大规模网络分析。更具体地说，网络中的半监督和监督学习、个性化和推荐、信息扩散和表示学习。他拥有印度科学研究所(IISc)的硕士学位和明尼苏达大学的博士学位，都是计算机科学专业。Karthik获得了许多著名奖项，包括IBM博士奖学金、2013年SIAM数据挖掘(SDM)会议的最佳论文奖和2013年INFORMS Edelman桂冠奖。

参考文献：

Code Library: GraphZoo: Facilitating learning, using, and designing graph processing pipelines/models systematically.
Choudhary, N., Rao, N., Katariya, S., Subbian, K., & Reddy, C. K. (2022, February). ANTHEM: Attentive Hyperbolic Entity Model for Product Search. In Proceedings of the International Conference on Web Search and Data Mining 2022. (pdf)
Choudhary, N., Rao, N., Katariya, S., Subbian, K., & Reddy, C. (2021). Probabilistic Entity Representation Model for Reasoning over Knowledge Graphs. Advances in Neural Information Processing Systems, 34. (pdf)
Choudhary, N., Rao, N., Katariya, S., Subbian, K., & Reddy, C. K. (2021, April). Self-Supervised Hyperboloid Representations from Logical Queries over Knowledge Graphs. In Proceedings of the Web Conference 2021 (pp. 1373-1384). (pdf)
Chami, I., Ying, Z., Ré, C., & Leskovec, J. (2019). Hyperbolic graph convolutional neural networks. Advances in neural information processing systems, 32, 4868-4879. (pdf) Ganea, O. E., Bécigneul, G., & Hofmann, T. (2018). Hyperbolic neural networks. Advances in neural information processing systems, 5345-5355. (pdf) Shimizu, R., Mukuta, Y., & Harada, T. (2021). Hyperbolic neural networks++. Interna