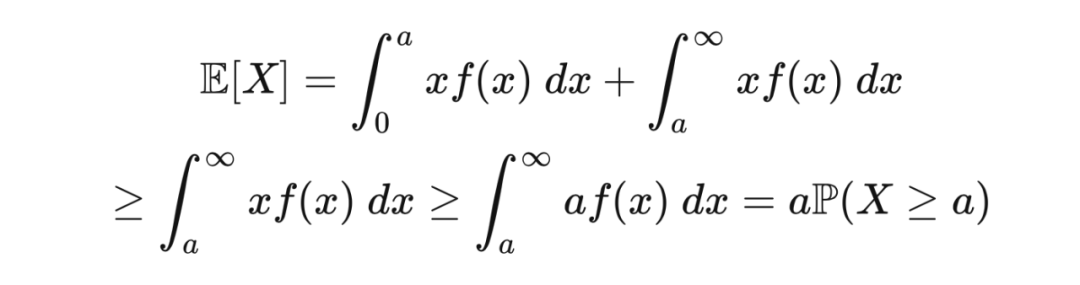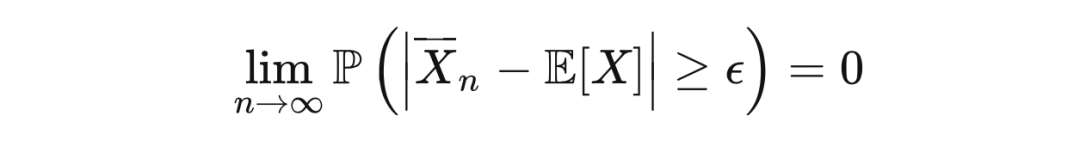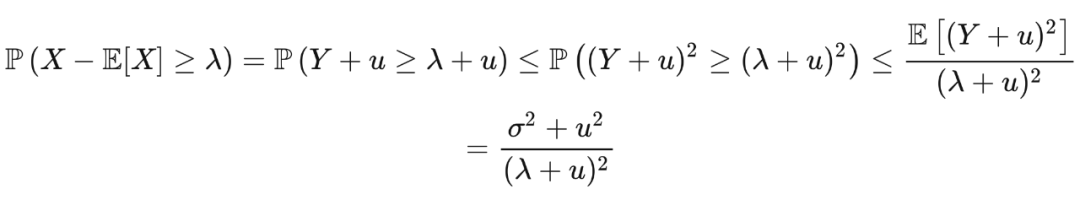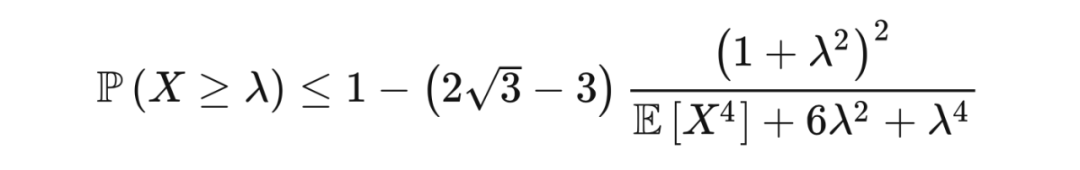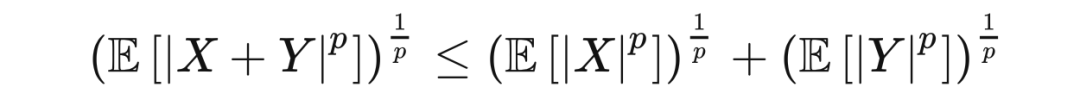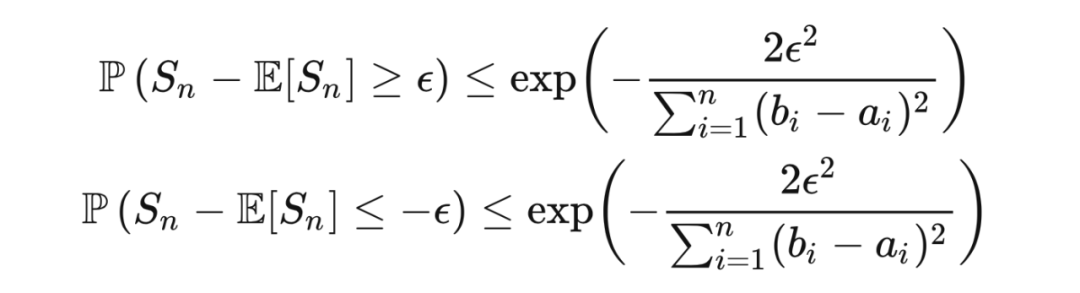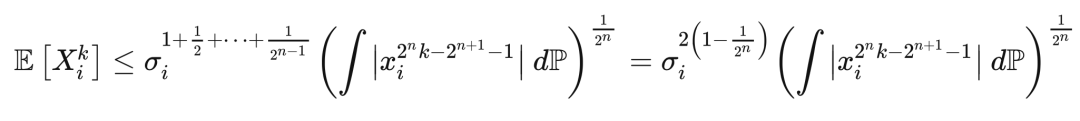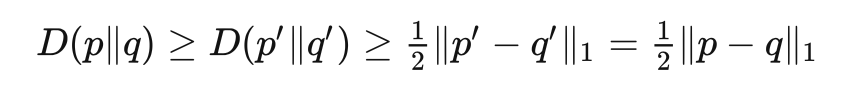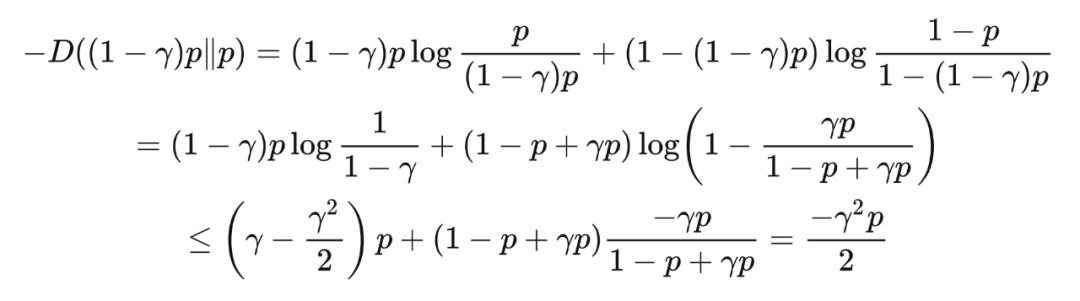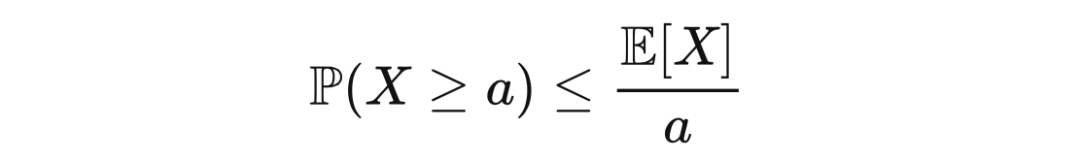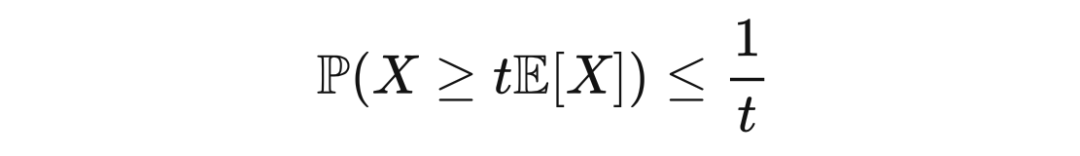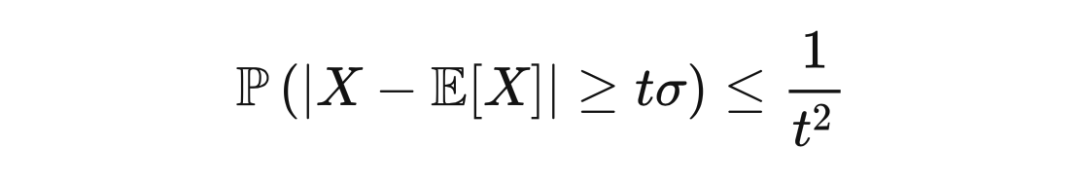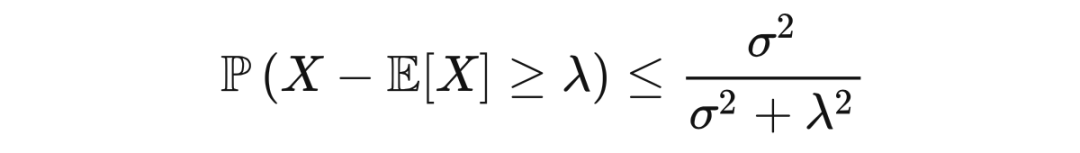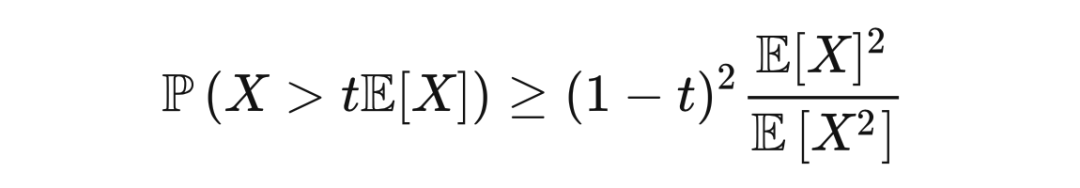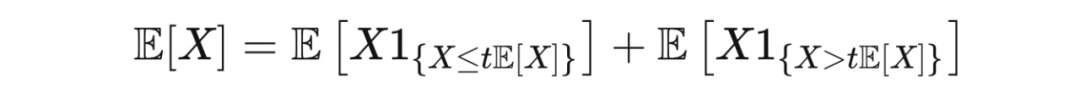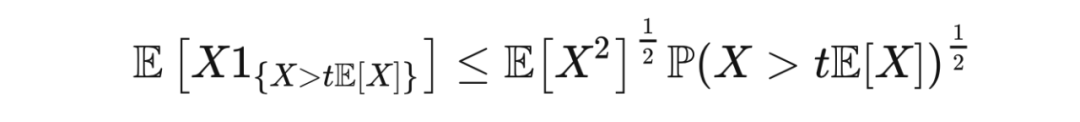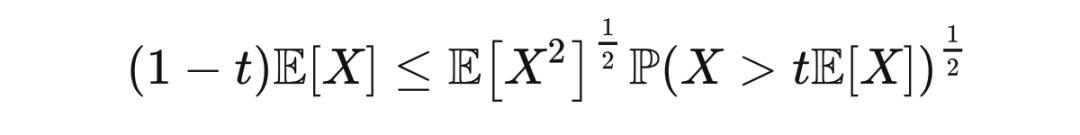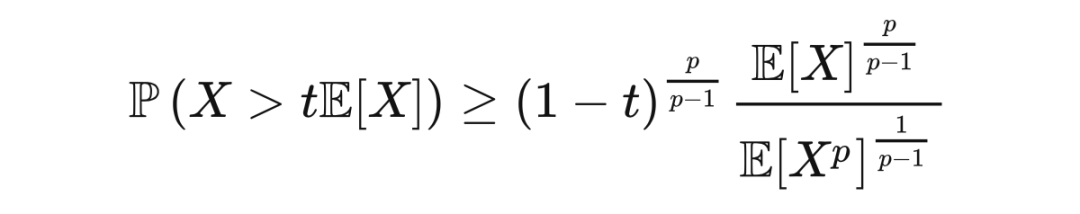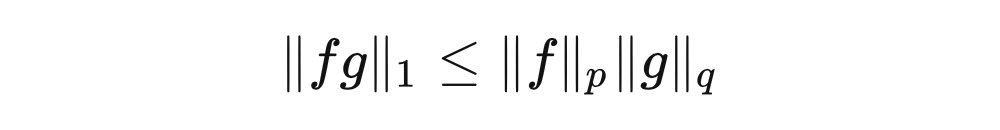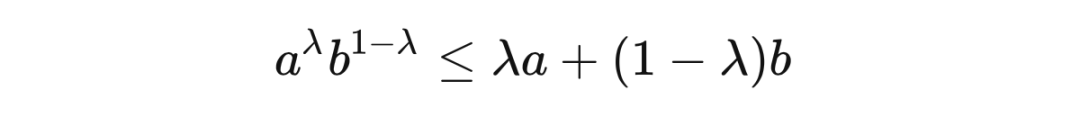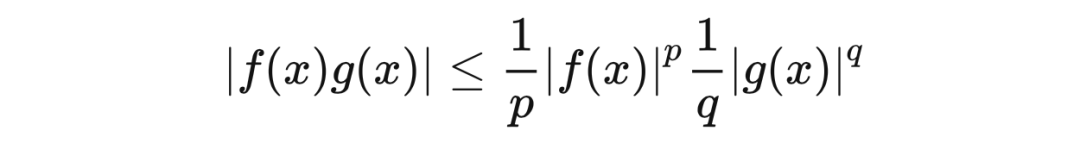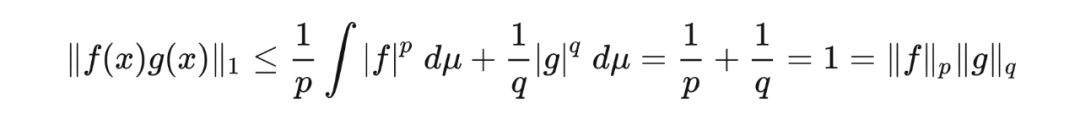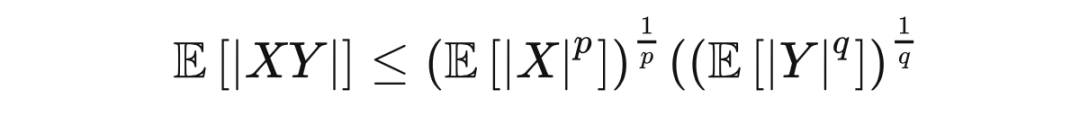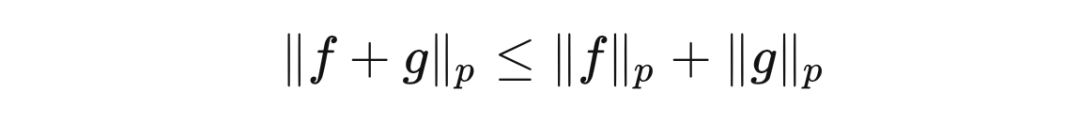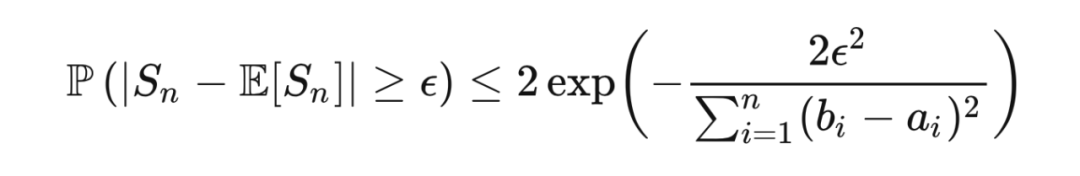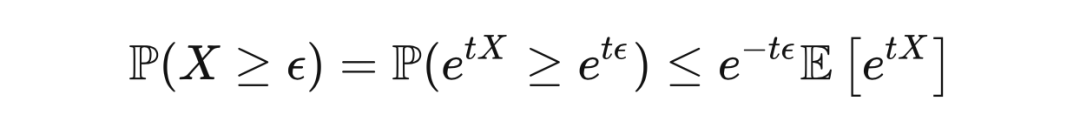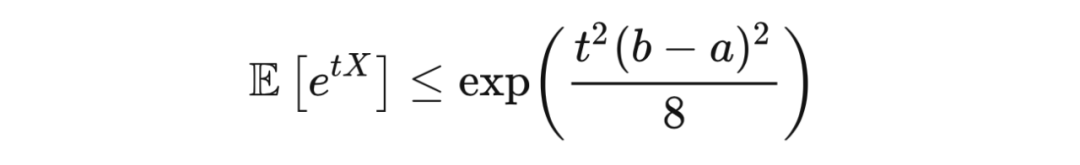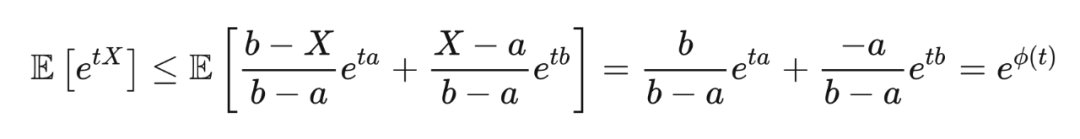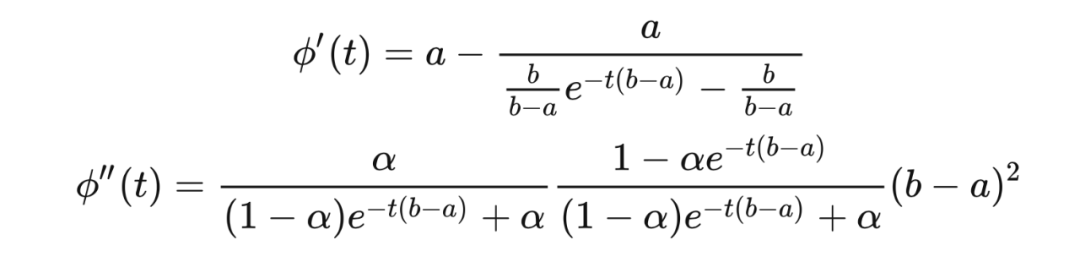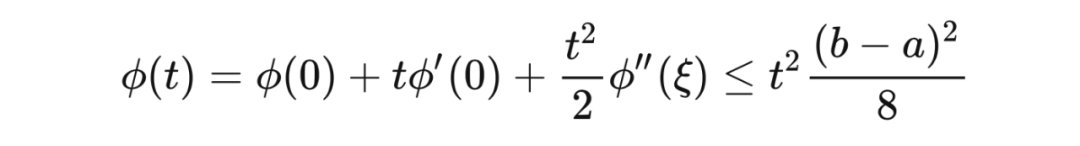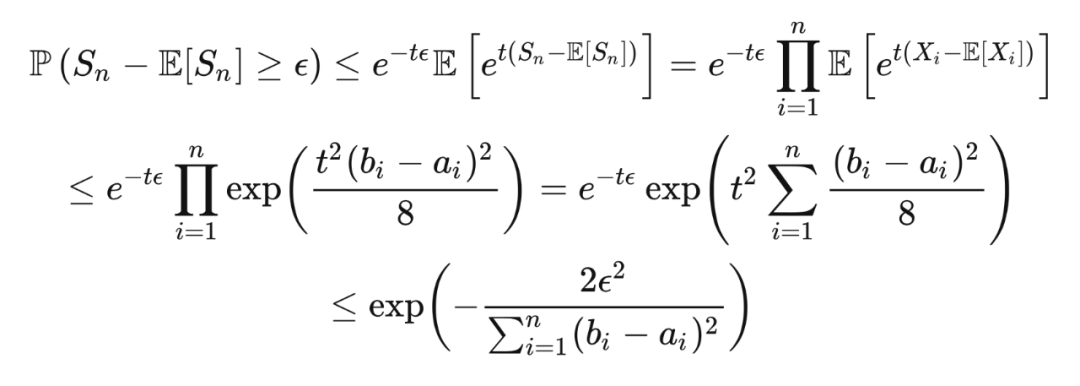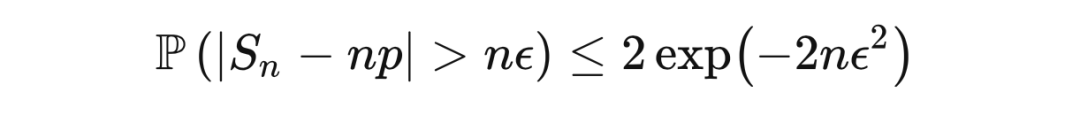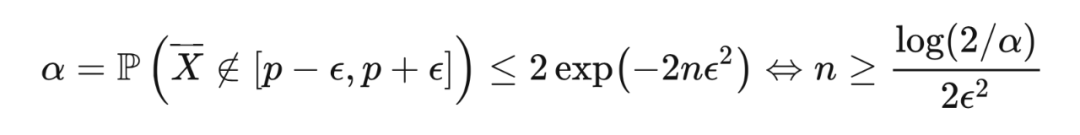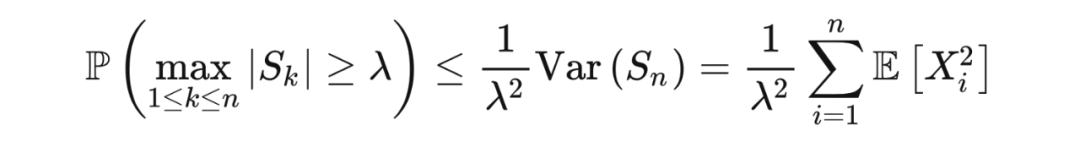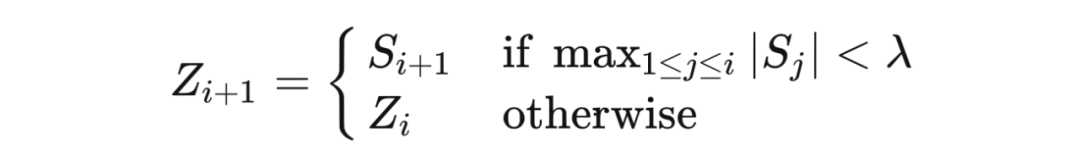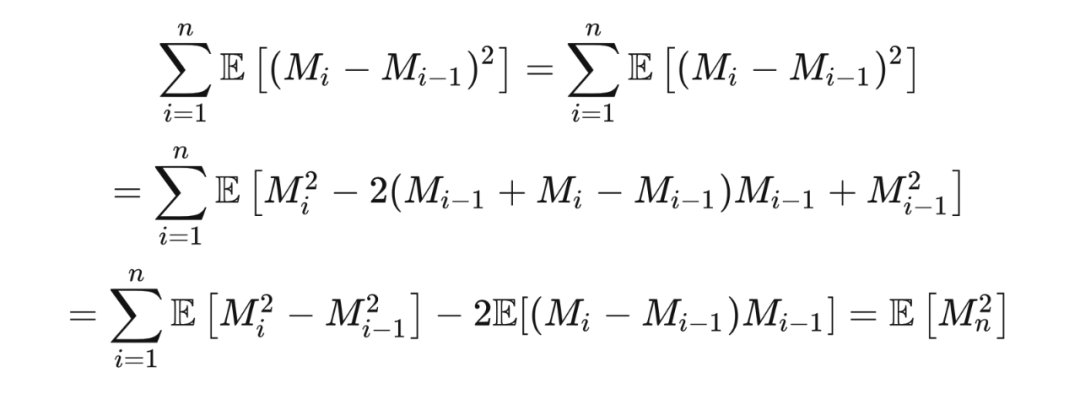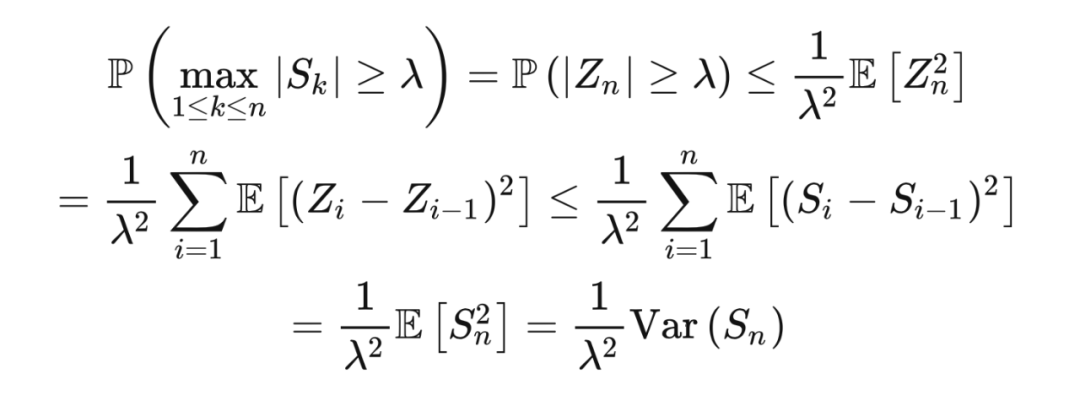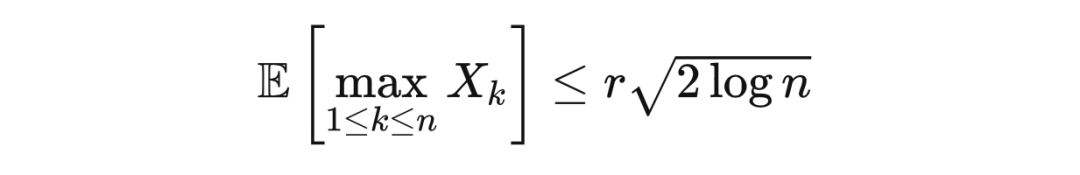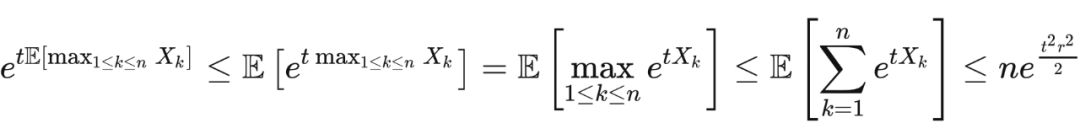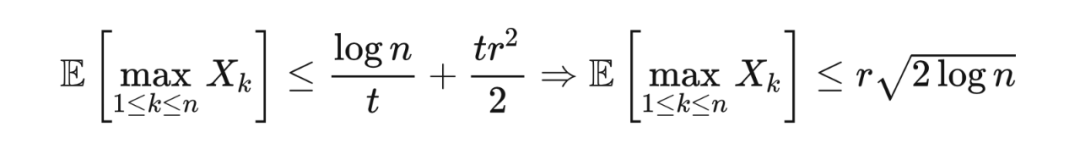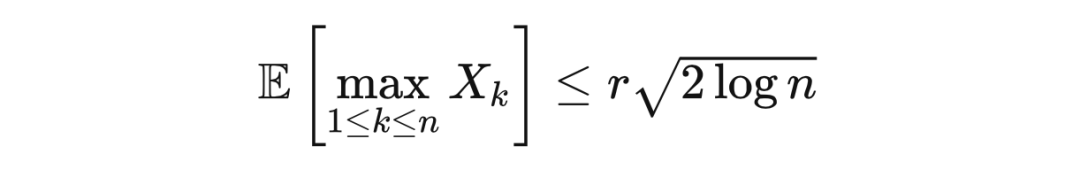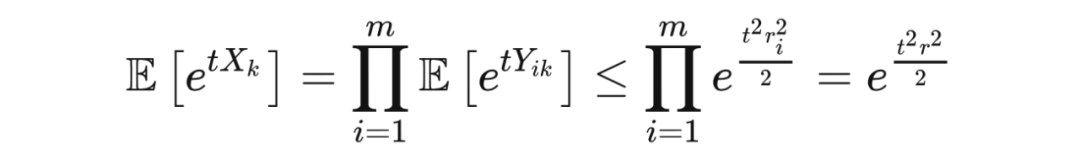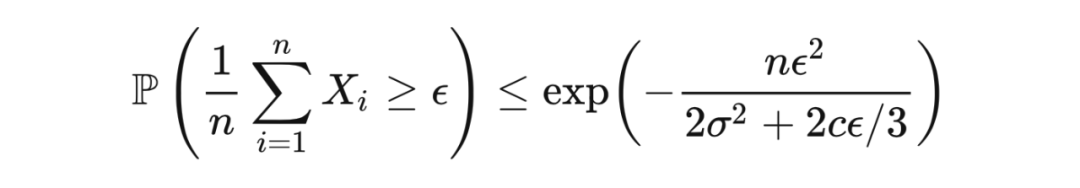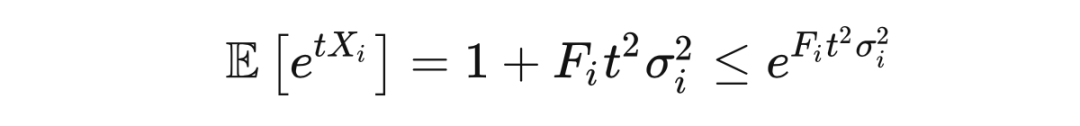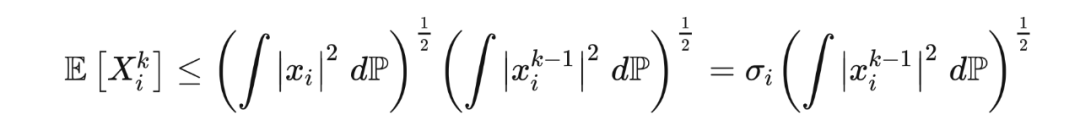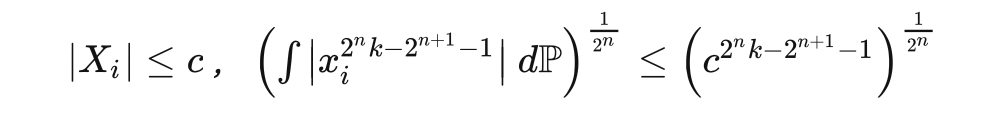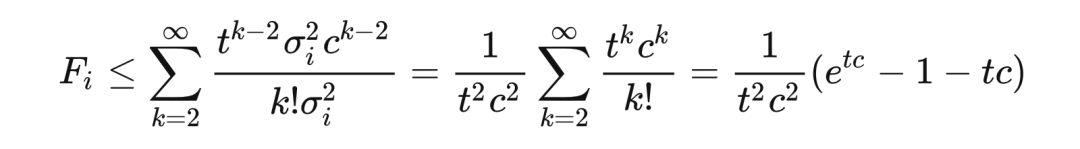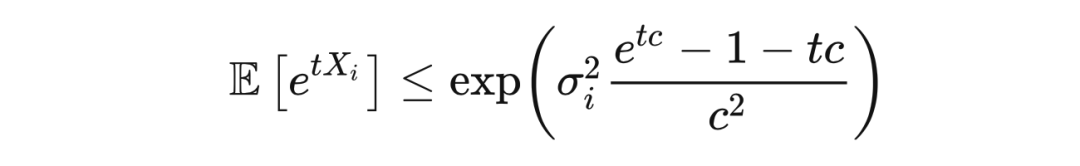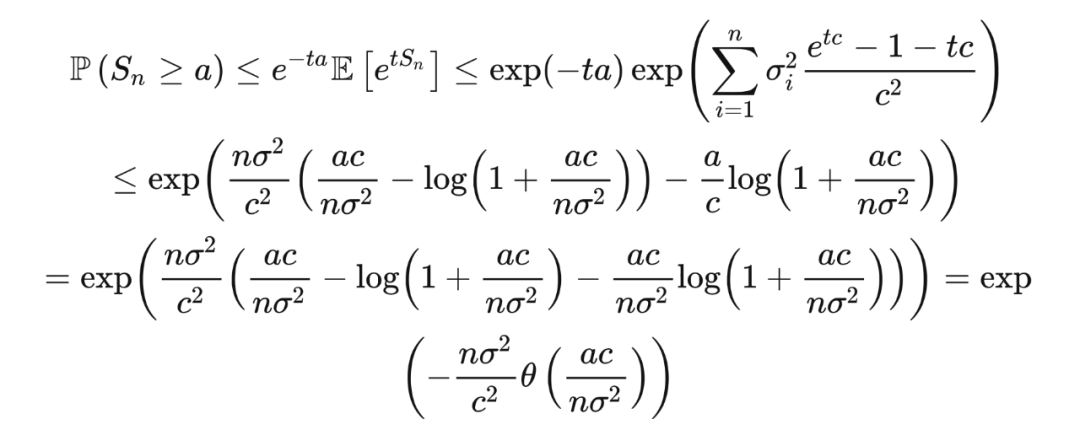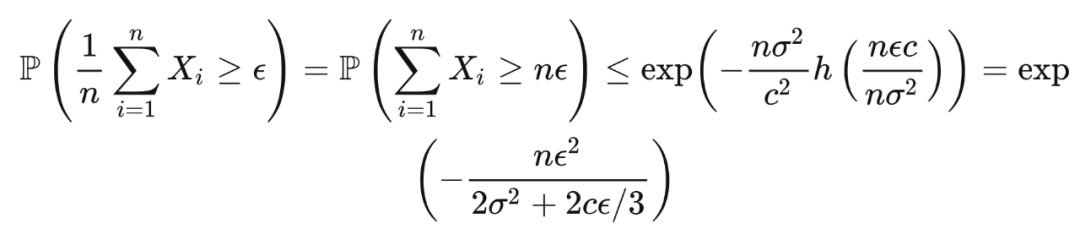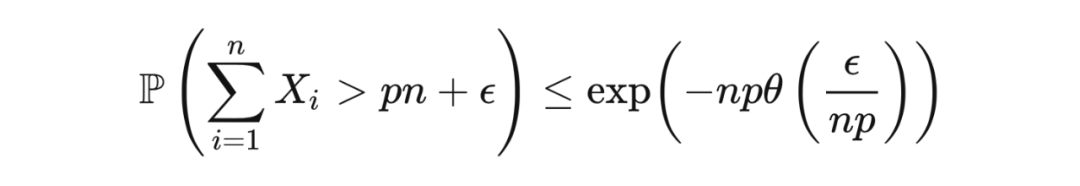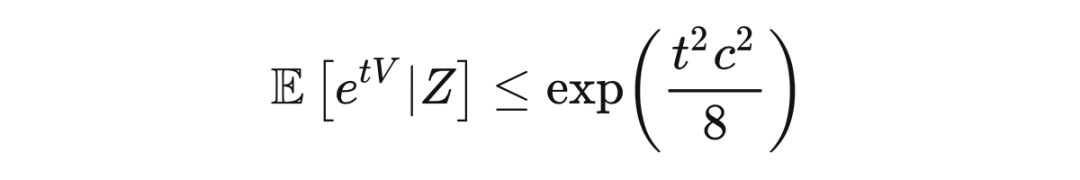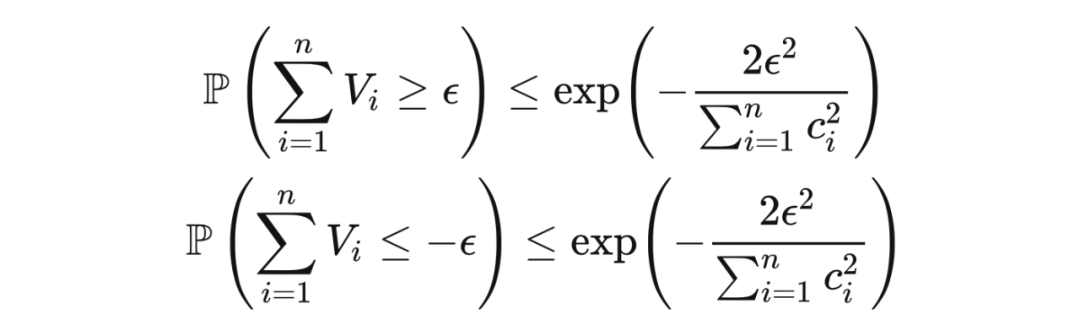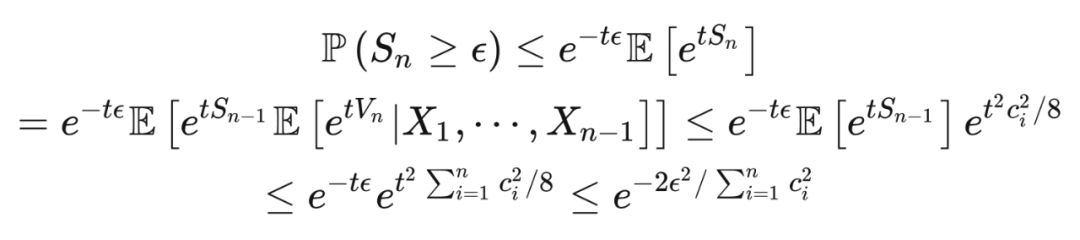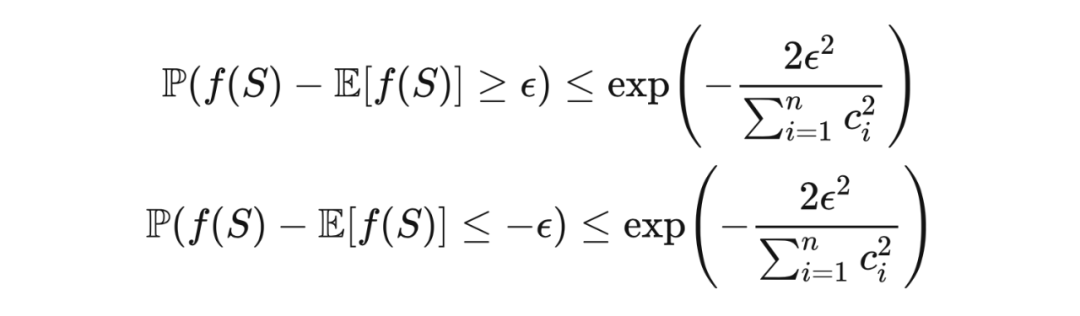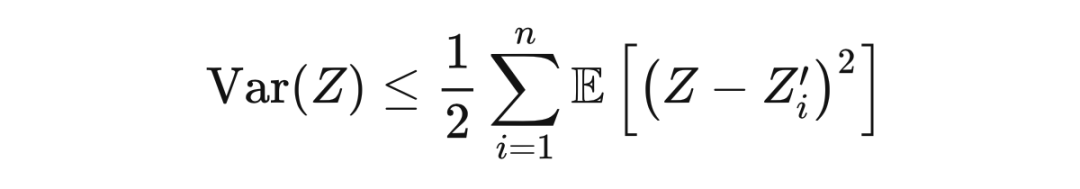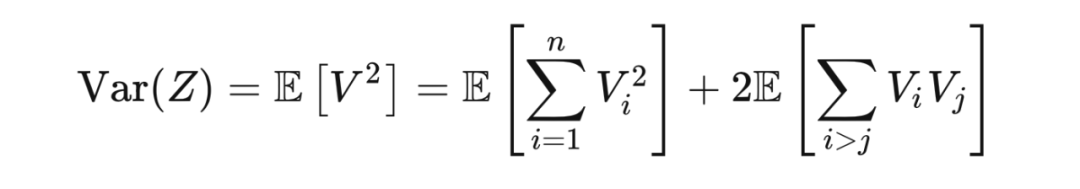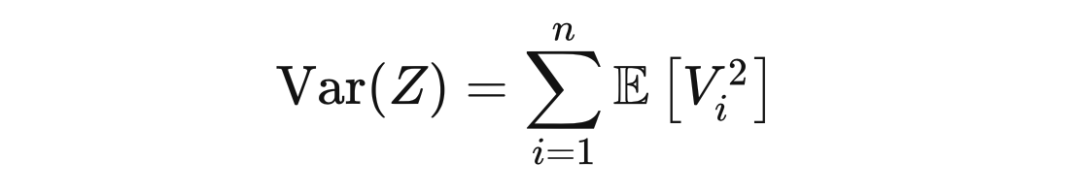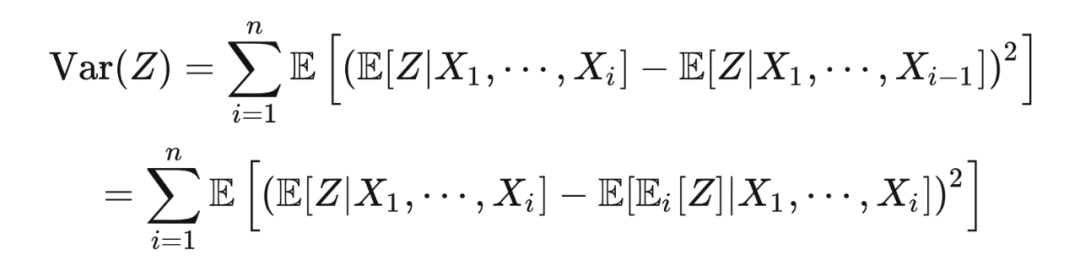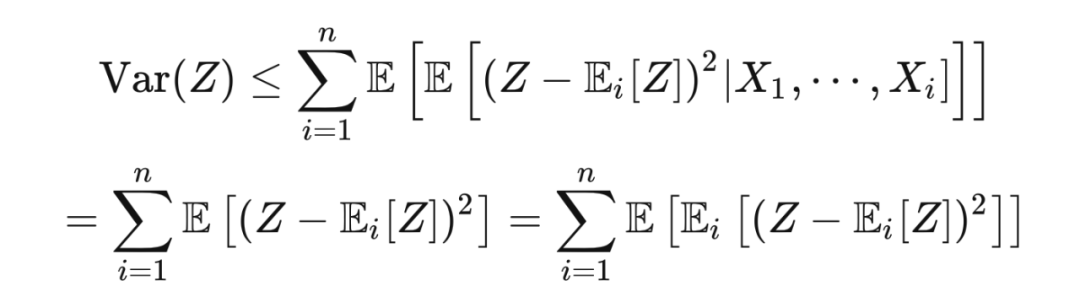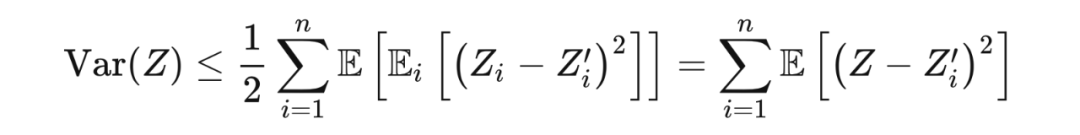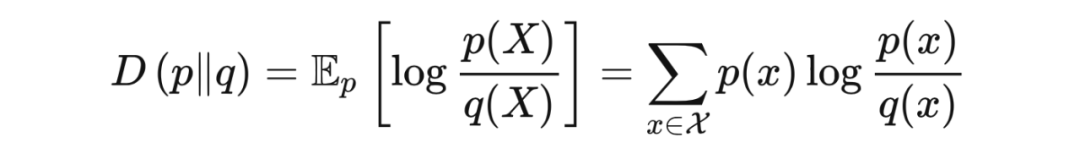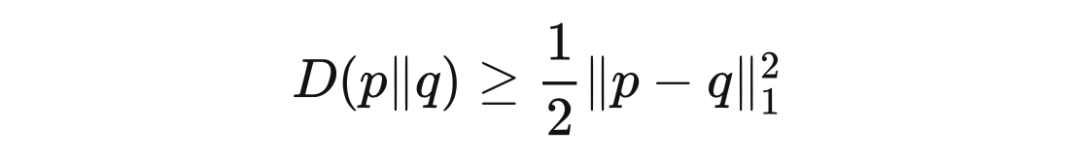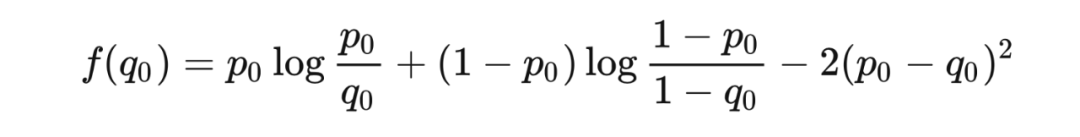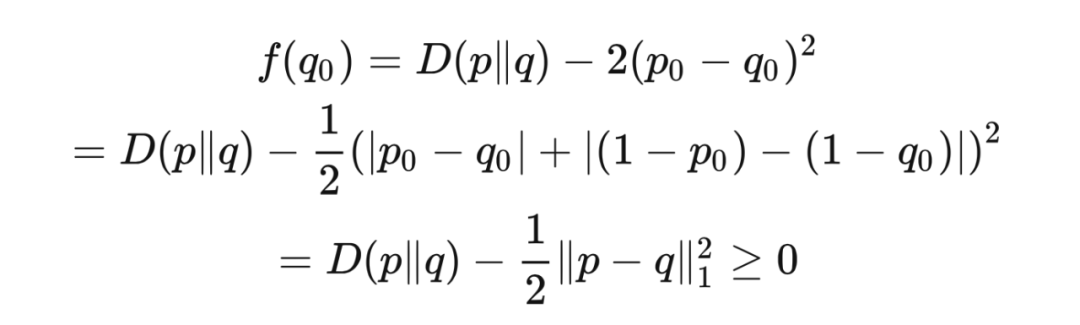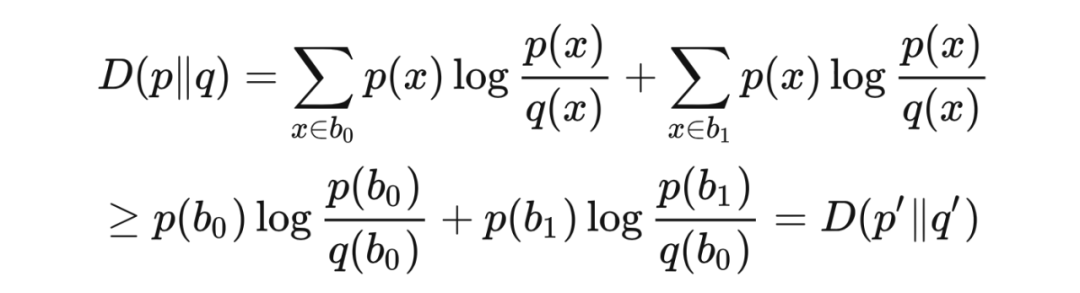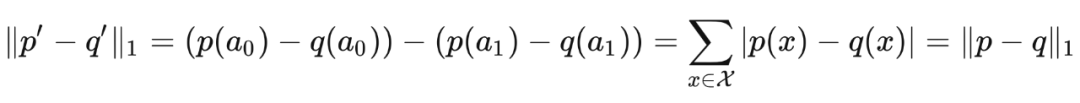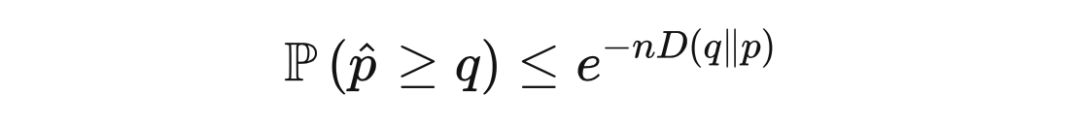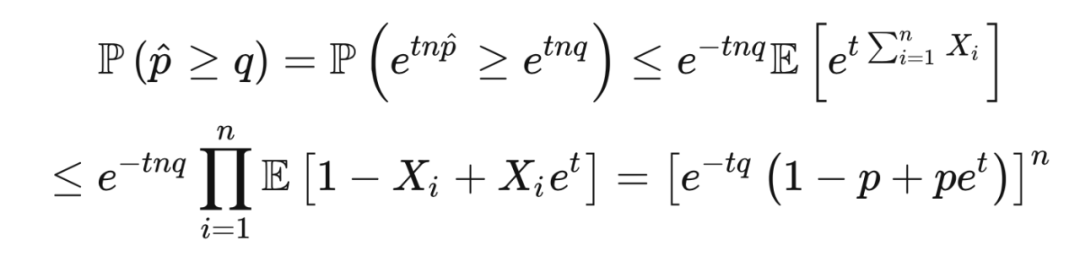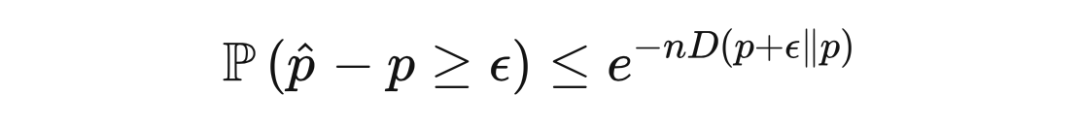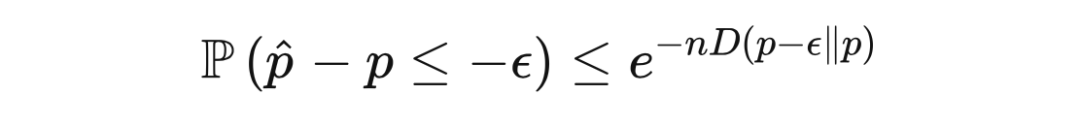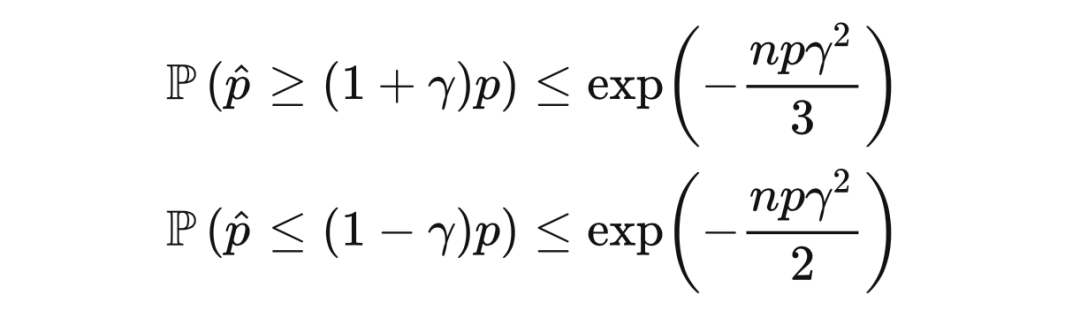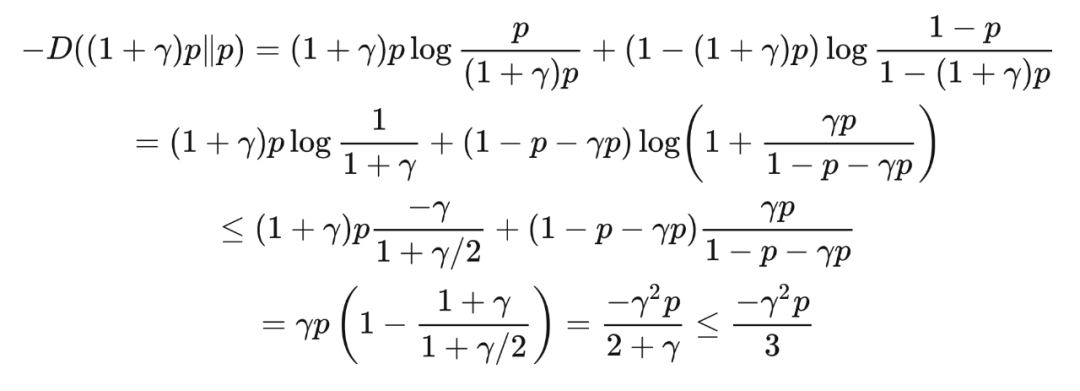概率论和机器学习中的不等式

©作者 | 斯宾王

在概率论（probability theory）中有很多优美且重要的不等式，它们常常被称作集中不等式（concentration inequality）。这些不等式为随机变量偏离（deviate）某些值的概率给出界（bound），因此它们常常在机器学习（machine learning）中起到评估估计量（estimate）的作用。

比如，应用霍夫丁不等式（Hoeffding's inequality），可以得到经验误差（empirical error）偏离真实误差（true error）的上界。马尔可夫不等式（Markov's inequality）和切比雪夫不等式（Chebyshev's inequality）是集中不等式中最有名的，也是最基础的。

马尔可夫不等式

著名的马尔可夫不等式为一个非负随机变量大于等于一个正值的概率给出了上界。此不等式以数学家马尔可夫命名，但由于它在马尔可夫的老师切比雪夫的工作中出现，也被称作切比雪夫不等式。为了和一般所指的切比雪夫不等式区分开，马尔可夫不等式被称作切比雪夫第一不等式，而一般所指的切比雪夫不等式被称作切比雪夫第二不等式。马尔可夫不等式如下所述。

定理 1.1（马尔可夫不等式） 若 是一个非负随机变量，且 ，那么

证明 由于 是非负的，所以 ，其中 是 的PDF（概率密度函数）。那么，

这样我们就得到了 。

在实际应用中，常数 通常被选定为 的期望的正数倍，这样马尔可夫不等式可被写作

这里 。举个形象的例子，若 是收入，那么收入超过 3 倍平均收入的人不超过总人数的 。

切比雪夫不等式

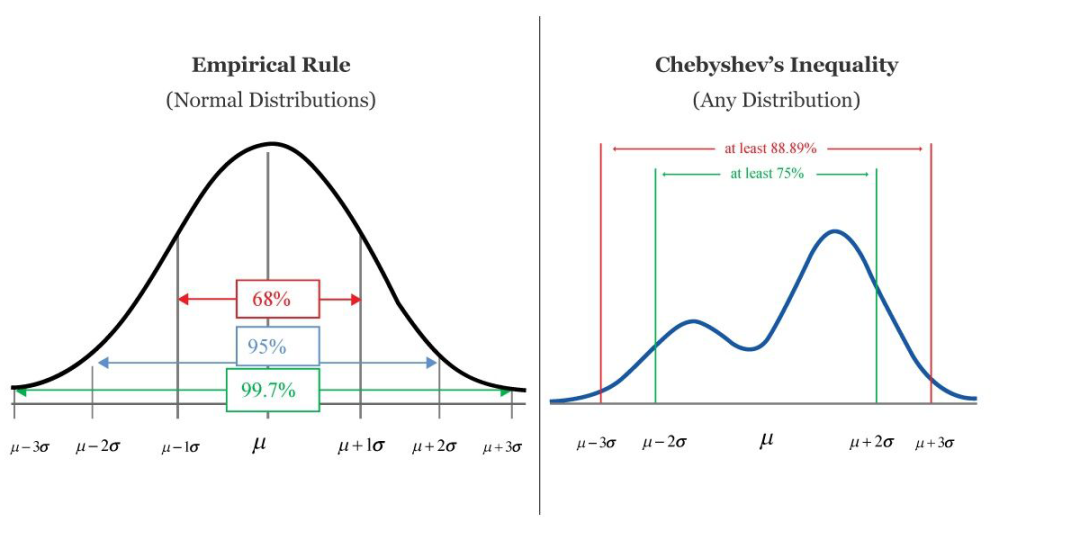
切比雪夫不等式指出，随机变量偏离其期望超过 个标准差的概率以 为界。切比雪夫不等式的用途和正态分布的 68−95−99.7 法则类似，但可以应对更一般的概率分布。此不等式保证，对于一系列范围很广的随机变量，有至少 75% 的值分布离期望两个标准差之内的范围当中，有至少 88.9% 的值分布离期望三个标准差之内的范围当中。切比雪夫不等式是马尔可夫不等式的直接推论。

▲ 68-95-99.7法则和切比雪夫不等式

定理 2.1（切比雪夫不等式） 若 是一个随机变量，其方差为 ，那么

证明 令 ，并令 。根据马尔可夫不等式，我们有

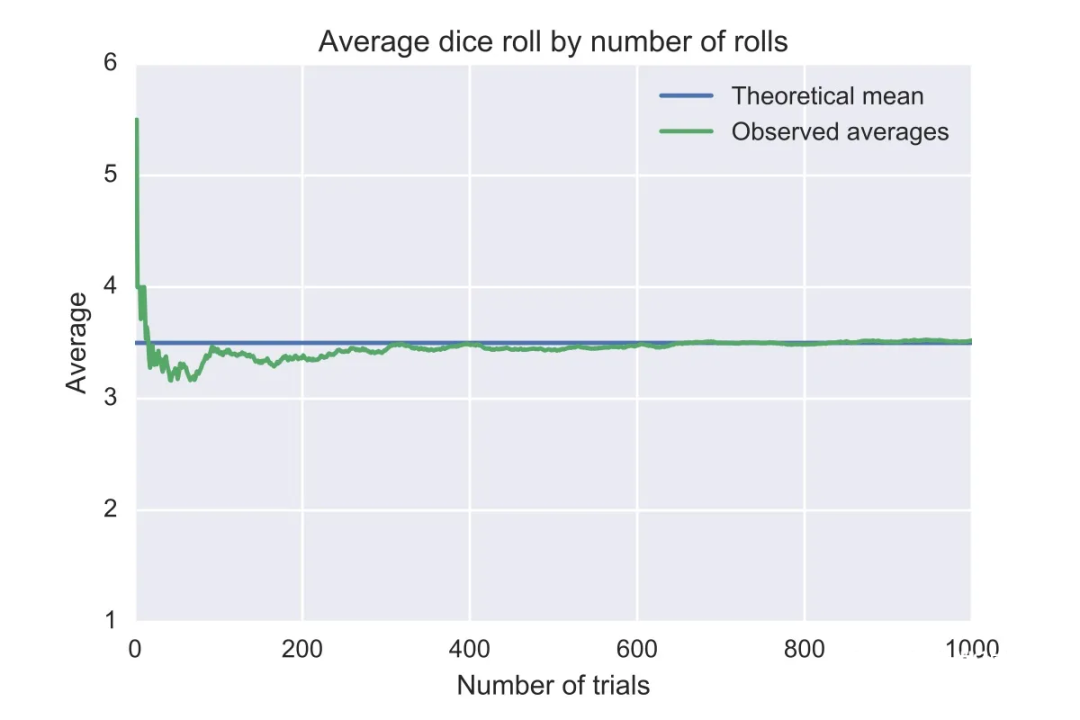
切比雪夫不等式的一个重要应用是证明弱大数定律（weak law of large numbers）。对于 ，其中 是独立随机变量，和任意 ，令 ，并应用切比雪夫不等式，我们就可以得到弱大数定律。

定理 2.2（弱大数定律 ） 令 为独立随机变量序列，其中所有 均值相等，且方差均为 ，并令 。那么，对于任意 ，

▲ 大数定律

坎泰利不等式

坎泰利不等式（Cantelli's inequality）是对切比雪夫不等式单边尾界（tail bound）的改进。尽管此不等式以数学家坎泰利命名，它在切比雪夫的工作中已经出现。

定理 3.1（坎泰利不等式） 若 是一个随机变量，其方差为 ，那么，对于 ，

证明 令 ，并令 。那么

其中第三个不等式是由于马尔可夫不等式。若选取 使得 最小，我们得到 。将此值代入上面的不等式，我们就得到了坎泰利不等式。

若选取 ，我们可以通过坎泰利不等式得到 和 。因此，坎泰利不等式表明，随机变量的平均数和中位数的差不会超过一个标准差。

切比雪夫不等式和坎泰利不等式用到的是随机变量的二阶矩（second-order moment），而若用到更高阶的矩，我们可以得到更强的不等式，比如何-张-张不等式。此不等式指出，若随机变量 满足 ，且 ，则

佩利-齐格蒙德不等式

前面的不等式为尾部概率给出了上界，而佩利-齐格蒙德不等式（Paley-Zygmund inequality）为尾部概率给出了下界。此不等式表述如下。

定理 4.1（佩利-齐格蒙德不等式） 若 是一个非负随机变量，且 ，那么

证明 我们将 分解为

第一项满足 。根据柯西-施瓦茨不等式（Cauchy-Schwarz inequality），第二项满足

这样，我们得到

整理后就是佩利-齐格蒙德不等式。

佩利-齐格蒙德不等式还有 版本：若 是一个非负随机变量， ，且 ，那么

赫尔德不等式

赫尔德不等式（Hölder's inequality）是 空间中的积分所满足的不等式。 空间是由这样的函数 所构成的空间：令 为一个测度空间（measure space），函数 是可测的（measurable），且它的 范数（norm） 满足 。赫尔德不等式的表述如下。

定理 5.1（赫尔德不等式） 假设 ，且 。若 是定义在 上的可测函数，那么

特别地，如果 且 ，则 ，且等式成立当且仅当 ，其中 为满足 的常数。

证明  我们首先证明一个工具性不等式：若 ，且 ，则

等式成立当且 。若 ，结论无需证明。若 ，将不等式两边同时除以 ，并令 ，我们要证明的结论变为 ，等式成立当且仅当 。由于 在 时严格单调递增，并在 时严格单调递减，所以 在 时达到最大值，而最大值正是 。

若 或 ，或者 或 ，结论无需证明。此外，若结论对于 成立，则结论对于 的标量倍数成立。因此，我们只需证明不等式当 是成立，等式成立当且仅当 令 ，并令 。根据之前证明的工具，我们有

不等式两边同时积分，得到

等式成立当且仅当 ，而根据之前证明的工具，这等价于 。

概率论中的赫尔德不等式表述如下：若 是一个概率空间，且 是期望算子（operator），则实值或复值随机变量 满足

赫尔德不等式的一个推论是闵可夫斯基不等式（Minkowski inequality），即 空间中的函数所满足的三角不等式（triangle inequality）

这里 ， ，且 。若用概率论的语言表达，此不等式是

霍夫丁不等式

对于有界独立随机变量之和 ，霍夫丁不等式（Hoeffding's inequality）给出了 偏离其期望的概率的上界。若随机变量 在区间 上取值，那么霍夫丁不等式说指出， 个随机变量之和 满足

我们在不等式的证明中常常需要用到切尔诺夫边界技巧（Chernoff bounding technique）：对于任意 ，先用马尔可夫不等式得出

再为 找到上界 ，然后选择 对 进行最小化。对于霍夫丁不等式，我们所需的上界由霍夫丁引理（Hoeffding's lemma）给出。

引理 6.1（霍夫丁引理） 若 ，且 ，则对于任意 ，有

证明 由于 是一个凸映射，对于任意 ，有 。由于 ，

其中：

通过计算，我们得到：

其中 。注意 ，且 ，这里 。由于 ， ，故 。根据泰勒定理（Taylor's theorem），存在 ，使得

接下来我们证明霍夫丁不等式。

定理 6.2（霍夫丁不等 式） 若随机变量 是独立的，且每个 在区间 上取值，那么对于任意 和 ，

证明 应用切尔诺夫边界技巧和霍夫丁引理，我们有

这里第一个不等式是马尔可夫不等式，第一个等式是因为独立性，第二个不等式是因为霍夫丁引理，最后一个不等式是因为取 来对上界进行最小化。

霍夫丁不等式可以用于给出置信区间。假如一个特制的硬币正面朝上的概率是 ，我们投 次硬币，并得到 个样本 。令 为观察到的正面朝上的次数，则霍夫丁不等式给出

令 为观察到的均值，我们想构造一个长度为 且置信水平为 的关于 的置信区间。由于

我们至少需要 个样本，才能构造出 -置信区间 。

柯尔莫哥洛夫不等式

柯尔莫哥洛夫不等式（Kolmogorov's inequality）又被称作最大值不等式（maximal inequality），它为随机变量的部分和（partial sum）的绝对值的最大值的尾部概率给出了上界。

定理 7.1（柯尔莫哥洛夫不等式） 若随机变量 是独立的，且所有 均值为 0 ，方差是有限的，那么，对于 ，

这里 。

证明  由于序列 由均值为 0 的独立随机变量组成，序列 构成一个鞅（martingale），即 。定义 ，并令

由于序列每个 都是某个 ，所以 构成一个鞅. 对于任意鞅 ，若 ，则

这里： 

因此：

其中第一个不等式是因为切比雪夫不等式。

最大值不等式

除了柯尔莫哥洛夫的最大值不等式，我们再介绍两个关于随机变量的最大值的期望的不等式。对于满足一定条件的随机变量，这两个不等式中的上界由样本数的对数决定。

定理 8.1（最大值不等式） 令 为实值独立随机变量，使得对于任意 和 ， ，其中 。那么，

证明 任选 。由于指数函数是凸函数，根据詹森不等式，我们有

不等式两边同时取对数，再选取 使得右边的表达式最小化，我们得到

推论 8.2（最大值不等式） 令 为实值随机变量，使得对于任意 ， ，其中 是均值为 0 且在 取值的独立随机变量，这里 。那么

这里 。

证明 由于对于固定的 ， 是独立的，所以

其中 。这里的不等式是因为霍夫丁引理。应用定理 8.1，证毕。

伯恩斯坦不等式

霍夫丁不等式没有用到关于随机变量的分布的信息，而伯恩斯坦不等式（Bernstein's inequality）利用随机变量的方差给出了一个更紧的界。

定理 9.1（伯恩斯坦不等式） 令 为独立随机变量，使得对于任 意 ， ， 且  。 令  ， 则

证明 令 。 对于 ，令 。由 于 ， 且  ， 我们有

由于 ，根据柯西-施瓦茨不等式（Cauchy-Schwarz inequality），有

递归地应用柯西-施瓦茨不等式，我们有

由于

故 。令 ，我们得到  ， 所以

那么，

令  且 ，应用切尔诺夫边界技巧，我们得到

其中 。这里第一个不等式是马尔可夫不等式，第二个不等式是因为 ，第三个不等式是因为取 来对上界进行最小化。

令 和 。很容易证明， ，且 ，故 。令 ，我们得到

事实上，霍夫丁不等式、吾妻不等式和切尔诺夫界都是伯恩斯坦不等式的特例。

班纳特不等式

在伯恩斯坦不等式的证明的中间步骤中，我们证明了不等式

而这就是班纳特不等式（Bennet's inequality）。

定理 10.1（班纳特不等式） 令 为独立随机变量，使得对于任意 ， ，且 。令 ，则

其中 。

举例来说，若 是概率为 的独立的二元（binary）随机变量，那么班纳特不等式给出

相比之下，霍夫丁不等式给出的界是 ，伯恩斯坦不等式给出的界是 。

吾妻不等式

吾妻不等式（Azuma's inequality）给出了一个比霍夫丁不等式更普遍的结果，它是一个关于鞅差（martingale difference）的不等式。

定义 11.1 若在随机变量序列 中，每个 都是关于关于随机变量 的函数，且 ，则称 是关于 的一个鞅差序列。

下面的结论和霍夫丁引理类似，证明过程近乎一致，只是把期望替换为条件期望，并选取 和 。

引理 11.2 若随机变量 满足 ，且存在函数 和常数 ，使得 ，那么对于任意 ，有

现在我们来推导吾妻不等式。

定理 11.3（吾妻不等式） 令随机变量序列 为关于随机变量序列 的一个鞅差序列. 若对于所有 都存在常数 和作为关于 的函数的随机变量 ，使得 ，那么对于任意 和 ，

证明 对于任意 ，令 。应用切尔诺夫边界技巧和引理 11.2，我们有

这里第一个不等式是马尔可夫不等式，第一个等式是因为塔性（tower property），第二个不等式是因为引理 11.2，最后一个不等式是因为取 来对上界进行最小化。

现在我们来看一个简单的例子。若令 为 i.i.d 随机硬币投掷，那么由于 满足 ，吾妻不等式给出 。设 ，则 ，即 距 0 偏离大于 的概率随 趋向于 0 。

麦克迪尔米德不等式

麦克迪尔米德不等式（McDiarmid's inequality）是机器学习中很重要的一个不等式，对于关于独立随机变量的函数的样本值与期望值的偏离，它给出了界。此不等式成立的条件是有界差性质（bounded difference property），即当我们只改变多元函数的一个变量时，函数值的差不能太大。对麦克迪尔米德不等式的证明用到了吾妻不等式。

定理 12.1（麦克迪尔米德不等式） 令 为一组独立随机变量. 假设存在常数 和函数 ，使得 ，这对于所有 和 都成立。那么，对于任意 ，

证明 按如下方式定义 ：令 和 ，对于 ，令 。注意 。 

此外，根据塔性质， ，故 。因此， 是一个关于 的鞅差序列。将 写为 ，我们可以定义 的上界和下界：

由于 满足有界差性质，有 ，故 。对 应用吾妻不等式 ，我们就可以得到麦克迪尔米德不等式。

麦克迪尔米德不等式可以从稳定性（stability）的角度来理解：若一个变量的改变对函数值的改变有限，则函数对于其均值的偏离是是指数有界的（exponentially bounded）。注意霍夫丁不等式是麦克迪尔米德不等式的特例，此时函数是 。

埃夫隆-施泰因不等式

埃夫隆-施泰因不等式（Efron–Stein inequality）对关于随机变量的函数的方差给出了界，它是已知的界中最紧的之一。

定理 13.1（埃夫隆-施泰因不等式） 令 为一个关于随机变量的函数，并令 为独立随机变量。令  ， 则

这里 ，且 和 的分布相同。

证明 令 . 令 和 ，对于 ，令 。

那么  ， 故：

根据塔性质：

还是因为塔性质，由于 ：

故 。那么，

根据塔性质，我们有

在第二个等式中，我们用到了：

由于 是一个凸映射，根据詹森不等式（Jansen's inequality） ，我们有

若 为相同分布的两个独立样本，则  。 令 和 ，则 ，故

注意，当 ，埃夫隆-施泰因不等式会变为等式。

平斯克不等式

平斯克不等式（Pinsker's inequality）用 KL 散度（Kullback–Leibler divergence）为两个分布的总变分距离（total variation distance）给出了界。在引入此不等式之前，我们先介绍 KL 散度的概念。

定义 14.1  两个分布 和 的 KL 散度是

里我们令 ， ，且若 ， 。此外， ， ，这里 和 分别为分布是 和 的随机变量。KL 散度也叫作相对熵（relative entropy）。

由于詹森不等式（Jansen's inequality），KL 散度总是非负的。然而，KL 散度不是一个距离（distance），因为它不是对称的，且不满足三角不等式。平斯克不等式表明，两个分布的总变分距离以 KL 散度的函数为界。

定理 14.2（平斯克不等式） 对于两个分布 和 ，有

证明 我们首先证明此不等式对于在基数（cardinality）为 2 的一个集合 上的分布成立。令 和 。固定 ，并考虑映射 ，此映射由

定义. 注意 。对于 ，由于 ，而 ，当 ， ，当 ， 。那么， 在 处达到最小值，故 。用KL散度来表示 ，由于 和 ，我们有

这样我们就证明了，平斯克不等式对于在基数为 2 的集合上的分布成立。现在考虑在集合 上的分布 和 ，这里  ， ， ， 。

注意 和 是定义在 和 两个元素上的分布，而 和 是定义在集合 的单个元素上的分布。根据对数和不等式（log-sum inequality） ， 我们有

此外，我们还有

所以，我们得到，

萨诺夫定理

萨诺夫定理（Sanov's theorem）用KL散度给出了一个比霍夫丁不等式更精细的不等式。

定理 15.1（萨诺夫定理） 令 为独立随机变量，它们均值为 ，遵循以 为支撑（support）的分布. 那么，对于任意 ，

这里 ，且   为 和 的KL散度。

证明 由于 是一个凸映射，对于 ，。因此，

其中第一个不等式是因为马尔可夫不等式，第二个不等式是因为凸性质。若选取 使得 ，我们得到 。代入此值后，我们就得到了萨诺夫定理的不等式。

对于 ，令 ，通过萨诺夫定理，我们得到

萨诺夫定理给出了一个比霍夫丁定理更精细的上界，因为根据平斯克不等式， 。将此定理应用于 ，那么对于 ，令 ，我们得到一个对称的不等式

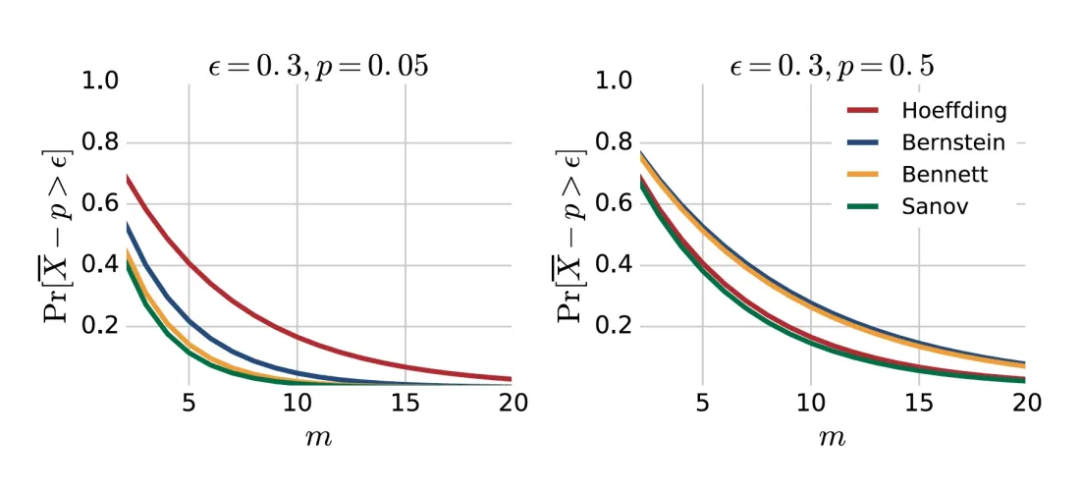
对于概率为 的伯努利试验（Bernoulli trial）的均值，霍夫丁不等式、班纳特不等式、伯恩斯坦不等式和萨诺夫不等式给出的尾部概率上界如下图所示。

▲ 对于概率为 p 的伯努利试验的均值，霍夫丁不等式、班纳特不等式、伯恩斯坦不等式和萨诺夫不等式给出的尾部概率上界

乘法切尔诺夫界

萨诺夫定理可以用来证明乘法切尔诺夫界（multiplicative Chernoff bound）。在霍夫丁定理的证明中，我们用到了切尔诺夫边界技巧，而乘法切尔诺夫界是关于相对误差（relative error）的。

定理 16.1（乘法切尔诺夫界） 令 为独立随机变量，它们均值为 ，遵循以 为支撑的分布。那么，对于任意 ，

这里 。

证明 我们要为 KL 散度找到一个比平斯克不等式中的界更精细的下界，这样我们就可以通过这个更精细的下界和萨诺夫定理得到乘法切尔诺夫界。根据不等式 和 ，我们得到

类似地，根据不等式   和 ，我们得到

参考文献

[1] Mehryar Mohri, Afshin Rostamizadeh, Ameet Talwalkar. Foundations of Machine Learning.

[2] Stéphane Boucheron. Concentration inequalities: a nonasymptotic theory of independence.

[3] G. B. Folland, Real Analysis: Modern techniques and their applications, New York, Wiley. (1999).

[4] Cantelli F. (1910). Intorno ad un teorema fondamentale della teoria del rischio. Bolletino dell Associazione degli Attuari Italiani.

[5] Godwin H. J. (1964). Inequalities on distribution functions. New York, Hafner Pub. Co.

[6] Billingsley, Patrick (1995). Probability and Measure. New York: John Wiley & Sons, Inc.

[7] W. Hoeffding, ”Probability Inequalities for Sums of Bounded Random Variables”, Journal of the American Statistical Association, 58:13-30, 1963.

[8] B. Efron, C. Stein, ”The Jacknife Estimate of Variance”, Annals of Statistics, 9:586-96, 1981.

[9] J. Michael Steele, “An Efron-Stein Inequality for Nonsymmetric Statistics”, Annals of Statistics, Vol 14, No. 2, Pg 753-758, 1986

[10] C. McDiarmid, ”On the Method of Bounded Differences”, In Surveys in Combinatorics, LMS lecture. note series 141, 1989.

[11] G. Benett, ”Probability Inequalities for Sum of Independent Random Variables”, Journal of the American Statistical Association, 57:33-45, 1962.

[12] S.N. Bernstein, ”The Theory of Probabilities”, Gastehizdat Publishing House, Moscow, 1946.

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·