bert性能优化之——用另一种方式整合多头注意力

作者：邱震宇（华泰证券股份有限公司 算法工程师）

知乎专栏：我的ai之路

今天我想给大家介绍这样一篇论文：Multi-Head Attention: Collaborate Instead of Concatenate。作者均来自

洛桑联邦理工学院_百度百科 baike.baidu.com

看过我文章的同学肯定知道，我一直在关注bert模型的性能优化相关研究，而这篇论文正好是与transformer的性能优化相关，并且我认为它的方法不需要做太多的适配就能应用在预训练模型上面，实用性较高，因此推荐给大家。

众所周知，经典的transformer架构中采用了multi-head attention机制来引导模型从不同角度学习不同的语义信息，从各种实验对比中也能发现多头机制确实能够提升模型在NLP任务上的精度。然而，随着目前大规模预训练模型的普及，多头注意力机制在带来精度提升的同时，也增加了计算的成本，带来了性能上的限制。

因此最近两年，有些研究人员尝试从不同的维度去探讨是否能从多头机制上去优化transformer的性能。有些工作重点关注了多头中每个头的注意力到底捕捉了哪些语义信息，头与头之间捕捉的信息是否有冗余，例如这篇论文：Analyzing multi-head self-attention: Specialized heads do the heavy lifting, the rest can be pruned，提出了一种量化注意力头重要程度的方法。还有一些工作更加激进，提出了多头注意力机制是否有必要的疑问，例如这篇论文：Are sixteen heads really better than one。它对transformer中的每个头都做了消融实验，探讨了每个头在不同下游NLP任务上的作用，最后提出了一种迭代式地剪枝注意力头的方法。

与上述工作不同，本篇论文并非直接对注意力头进行结构性剪枝，而是关注所有注意力头捕捉的通用信息，试图将这些信息提取出来作为sharing weights，每个头各自关注自己独有的工作，从而减少多头注意力计算时的成本。下面我就详细得为大家解读这篇论文的工作。

单个注意力头的减负

在那篇经典的Attention is all you need论文中，对于注意力分数的计算是这样的：

其中，  当X和Y是同一个序列时，就是自注意力模型，此时  。

然而，在各种版本的transformer实现中，上述各种线性映射计算是附加bias的，即  ，其中  。因为在各种深度学习框架中，默认支持broadcasting，所以这里公式上引入了  ,相当于实现了broadcasting。

在引入了bias后，我们重新对  进行展开，可得：

备注一下：论文这里的公式貌似有点问题，最后一项应该是我推导出的项。

最后两项在做softmax的时候可以舍弃掉，为什么呢？其实很简单，我们得到的Attention分数是一个T*T的矩阵，而  和  得到的都是一个T*1的向量，最后通过  重复了T列扩充成了矩阵，因此每一行上，它的每一列的值都是相同的，因为softmax针对的是列维度，因此后两项对于整体的attention计算来说是一个常量，又因为：

  

因此最后两项计算可以舍弃。又因为前面两项中，不存在  ，因此我们甚至不用去定义这个bias项。

另外，对于上述推导式的第一项，由于其计算了Query和key的相互关系，因此相当于捕捉了上下文的相关信息，而第二项只包含了key的content信息，相当于捕捉了原文内容上的信息。

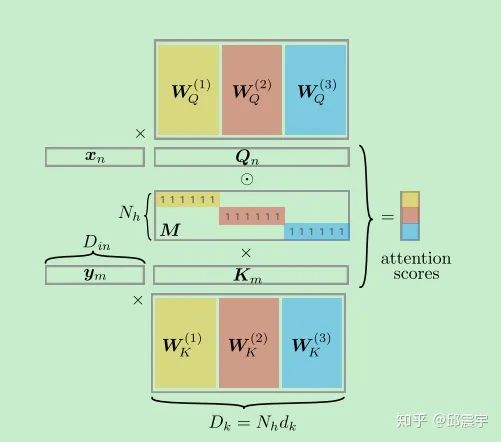
多头注意力的整合

传统的transformer中，对于不同的注意力采取的整合方式是直接拼接，如下所示：

其中，  表示注意力头的数量。我们再定义  为总的query/key的列空间维度，而  为每个注意力头中query/key的列空间维度。

根据过往的研究，我们可以发现所有注意力头之间捕捉的信息肯定是存在冗余的。单单研究不同头中key或者query映射矩阵的相似度是不够的，根据我们在单头注意力机制中的公式推导，可以知道，  同时捕捉了上下文的信息，因此可以对该项进行验证分析。论文考虑了如下一种情况，即假设两个注意力头中的key/query映射矩阵通过一个相同的旋转方阵  转换为相同的矩阵，即：

此时，两个头的注意力分数是相同的，因为：

 (R是一个旋转方阵，转置相当于逆旋转)。为了能够忽视引入旋转矩阵带来的人工误差，下面主要是分析不同头之间  的相似程度。论文设计了一种对比实验，对比A侧为对每个头上  做PCA分解后，计算不同主成分数量的累积variance值。对比B侧则是将所有头的  进行拼接后，对拼接后的矩阵做PCA分解，计算不同主成分数量上的累积variance值。

PCA之前我有文章科普过，相当于是找一个投影空间，让所有高维的点在这个空间上的投影尽量分开，即方差尽量大。因此variance代表了不同主成分上包含原始矩阵的信息量。variance越高，信息量就越多。

实验结果如图所示：

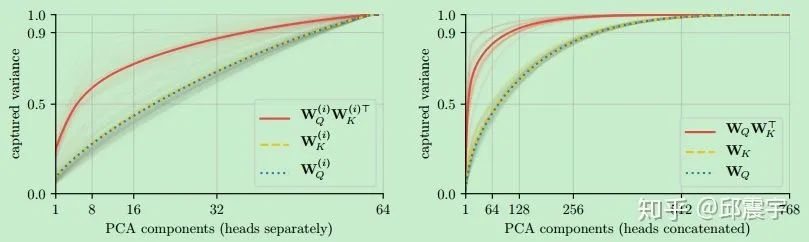
可以看到，右边图例上，对于拼接后的矩阵，其variance累积曲线很快就接近了1.0，表明其有一大部分成分包含的信息比较少，而左边图例上的曲线相对较为平滑，表明单个头上的  主成分包含的信息分布较为均匀。

从上述对比图例可以看出，头与头之间的通用信息还是比较多的。论文指出拼接后的  只需要大概1/3的维度就足够捕捉绝大部分的信息了。

提取通用信息

既然注意力头之间存在那么多的通用信息，那么如何进行实际操作将其单独提取出来呢？论文设计了一个混合向量，  ，  表示整合完所有注意力头之后的输出的映射矩阵维度。这个向量可以通过跟模型一起学习得到。然后我们将其代入原始的多头注意力计算中，得到：

其中  被所有注意力头共享。上述式子我们可以理解为用于捕捉所有注意力头之间的通用信息，而  则是帮助捕捉每个头各自独有的信息。上述整合方式有两种作用：

1、注意力头的表示方式更加灵活，注意力头的维度可以根据实际情况进行改变。的维度可以根据实际情况进行设置，若  ，则相当于传统的transformer形式，若  ，则相当于对transformer模型进行了压缩。

2、参数计算更加高效，是共享于所有的注意力头的，每一轮训练只需要计算一次。

明显可以看出来，原始的拼接方式做多头注意力机制是上述CollabHead方式的一种特例，此时  ，而  是一个由1和0两种元素组成的向量，其中1的元素位置为其对应注意力头的映射矩阵在拼接后的整体矩阵中的位置。如图所示：

其中，  。M使得模型在整合注意力头的时候，让每个注意力头之间都互相独立。

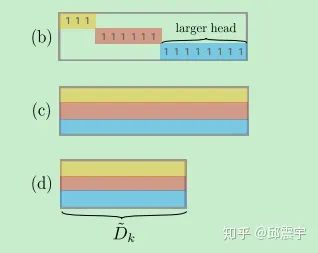
如果我们的目的是进行模型的压缩，提升模型性能，那么可以通过设计不同形式的M来实现，比如如下几种模式：

b模式相当于对不同的head抽取不同维度的矩阵信息；c模式则是让所有head都共享映射矩阵；d模式则是在共享映射矩阵的基础上，进一步压缩最终输出的整合矩阵的维度，达到压缩维度的效果。

实验

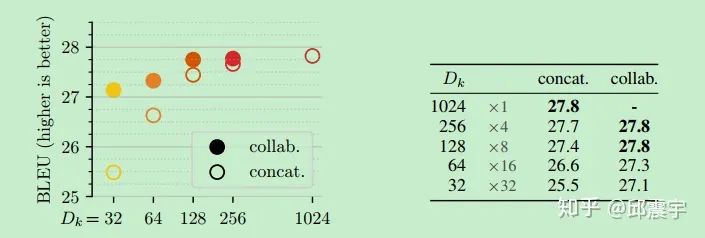
论文作者利用上述优化后的transformer架构进行了NMT的实验，主体网络为encoder-decoder，实验结果如下：

可以看到，collabHead在维度缩减到1/4时，仍然能保持跟原始维度相近的效果，说明经过压缩之后，模型只损失了较少的信息。

论文说到这里还没结束，下面要说的才是我比较关注的内容，即如何对预训练后的bert模型应用collabHead，从而提升bert的inference效率。

More collabHead on Bert

通过上述实验，已经能够证明CollabHead模式相比原始的简单拼接模式，在提升性能的同时，只会损失很小的精度。而Bert模型的主体架构也是transformer，因此它也可以利用这个优化达到性能提升的效果。最简单的方式就是在预训练的时候就采用这种架构，而论文也比较推荐这种方式。但是对于我们这种硬件条件有限制的企业来说，从头预训练一个模型似乎不太现实，那么有没有办法直接在finetune过程实施这种优化，从而达到性能提升的效果呢？

答案当然是可以的。论文提出了一种re-parameterize方式，直接对预训练模型中的attention权重进行张量分解，使得分解后得到的矩阵能分别对应上述优化中的各个参数。

该方法的主要核心为Tucker 张量分解，或者更具体得说是CP分解。（CP分解是Tucker分解的一种简化特例）。对于张量分解，可以参考其他博客中的讲解zhuanlan.zhihu.com/p/25 。这里就简单介绍一下。

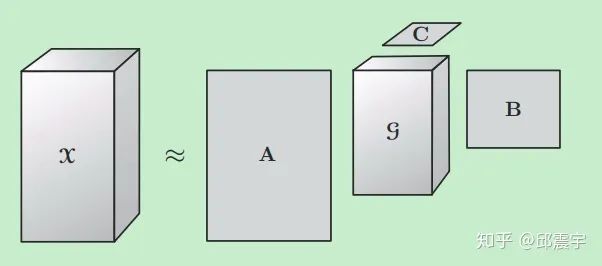
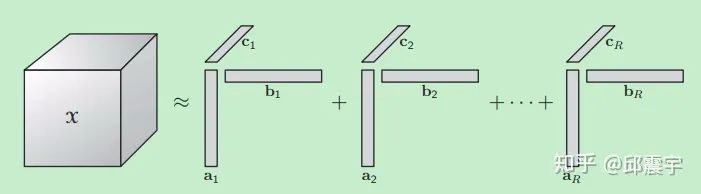
假设当前有一个张量  ,Tucker分解可以将该张量分解为如下形式：

,Tucker分解可以将该张量分解为如下形式：

其中，

  ，更具体的有：

 代表矩阵的外积。下图能够直观表示上述过程：图参考自sandia.gov/~tgkolda/pub

矩阵A，B，C通常称为因子矩阵，在一定程度上包含了原始X中各个维度上的主要信息，而矩阵G通常称为核张量，用于表征不同因子矩阵之间互相关联的程度。

回到我们的多头注意力优化问题上。我可以尝试对多头拼接后的key/query映射权重参数进行张量分解： 

 

然而我们可以对上述张量分解进行简化。由于我们关注的是不同注意力头中对齐后的映射矩阵上的值（简单来说就是head_1中的矩阵的第一个元素与head_2中的矩阵的第一个元素进行对比），因此可以令G中非对角线上的值均为0，另外我们期望分解后得到的矩阵列空间维度均为  ,可以通过该参数调节模型压缩的程度，此时可以令  。最后我们就得到一个超对角G，同时它也是一个立方，根据以上条件，可以将Tucker分解简化为CP分解，具体如下：

,其中  分别表示X不同维度上的因子向量，我们可以分别用因子矩阵A,B,C来表示对应所有因子向量的组合。具体来说，上述还可以表示为：

下图为其矩阵分解图例，看完应该会对上述分解有个直观的理解：图参考自sandia.gov/~tgkolda/pub

备注：张量分解其实也是一个优化问题，一般通过计算分解前和分解后矩阵对应元素的mse loss来进行优化学习。因此分解过程也是需要一定的时间成本。

那么接下来，我们可以通过分解  ，使其分解的目标矩阵分别对应  。另外，根据第一小节介绍的单注意力头的优化结果，结合CollabHead的注意力头整合方式，可以得到如下式子：

其中，第一项可以在预训练权重参数中拿取所有注意力头的 ，并通过stack操作得到 ，对其进行张量分解得到的三个矩阵，最后完成第一项的计算；第二项其实也很简单，对每个注意力头，令  ,我们只需要拿到预训练权重参数中的对应参数，并计算得到  就可以了。

当然整体的re-parameterize操作除了上述步骤外，还有一些应用的小技巧。在实际应用时，通常按如下步骤进行：

1、使用原始的bert模型对下游任务进行finetune，得到一个finetune-bert-task模型。

2、对finetune-bert-task进行re-parameterize操作，得到压缩后的re-finetune-bert-task模型。

3、使用re-finetune-bert-task模型对下游任务再进行少量迭代的finetune。

经过实验验证，步骤3对于最后模型的精度还是很有帮助的，建议保留。

实验验证

我本来是想将该方法在我的NER任务中进行实际验证，但是发现好多张量分解的工具在tensorflow的静态图（尤其是estimator模式）下不太适配。如果有的同学对这方面实现兴趣，可以看一下tensorly框架，它支持tensorflow2.0的动态图模式、pytorch以及MXNET，在github上的一个issue上搜到其貌似也支持静态图，配置如下：

import tensorly as tl

tl.set_backend("tensorflow_graph")

另外还有一个框架tensorD,我试了一下也有bug。好在论文作者非常良心得放出了基于pytorch的开源代码，链接如下：github.com/epfml/collab。核心内容主要在两个文件：collaborative_attention.py 以及swap.py。前者主要定义了CollabHead的优化逻辑。后者则是定义了如何将预训练模型中的权重参数进行re-parameterize。下面主要看一下re-parameterize的内容。代码如下：

new_layer = CollaborativeAttention(
            dim_input=layer.dim_input,
            dim_value_all=layer.dim_value_all,
            dim_key_query_all=dim_shared_query_key,
            dim_output=layer.dim_output,
            num_attention_heads=layer.num_attention_heads,
            output_attentions=False,
            attention_probs_dropout_prob=layer.attention_probs_dropout_prob,
            use_dense_layer=layer.use_dense_layer,
            use_layer_norm=layer.use_layer_norm,
            mixing_initialization=MixingMatrixInit.CONCATENATE,
        )
_, factors = parafac(
                WQWKT_per_head.detach(), dim_shared_query_key, init="random", tol=tol
            )
WQ_shared, mixing, WK_shared = factors
new_layer.key.weight.data.copy_(WK_shared.transpose(0, 1))
new_layer.query.weight.data.copy_(WQ_shared.transpose(0, 1))
new_layer.mixing.data.copy_(mixing)

首先，定义出带CollabHead结构的attention模型，然后调用了tensorly的CP分解parafac方法，得到三个因子矩阵。最后分别将三个矩阵权重参数赋给计算图中对应的变量中。

bq_per_head = layer.bQ.reshape([layer.num_attention_heads, -1])
content_bias = bq_per_head.unsqueeze(1) @ WK_per_head
content_bias = content_bias.squeeze(1)
new_layer.content_bias.weight.data.copy_(content_bias)

上述操作即  的部分。

我在GLUE的MRPC任务上进行了实际的验证，结果如下：

1、对于精度损失而言，原始的bert模型在验证集上的f1大概是88。对re-parameterize后的bert模型再进行finetune后，其在验证集上的f1大概是86。虽然跟论文中的结果有些差距，但是精度损失还是比较可观的。

2、对于性能提升而言，我是将原始的隐层维度768减去一半。整体来说，inference的性能大概有30%左右的提升。但是我得提一点，就是在做张量分解的时候，论文中只要几分钟，可是我对12层的attention做了张量分解，总共花了有18分钟，虽然对训练的效率并没有拖太多后腿，但是跟论文数据确实是有点差距，后续还是要深入tensorly框架研究一下其内部机制。

3、简单说一下该方法与原始transformer在模型参数上的一些对比。原始的attention head计算机制在忽略bias的情况下，参数量为  ，本论文中的由于增加了混合向量，因此参数量为 ，我们可以通过控制  的大小来控制压缩程度。另外增加的  参数，因为注意力头数值通常比隐层维度数值小很多，因此其带来的参数量增加在一定程度上可以被低消。在计算的FLOPS对比上，原始的计算机制的FLOPS为  ，而本论文中的方法为  ,因为  ,因此两者FLOPS的比率为  。

另外，根据论文所说，该方法还可以与其他模型压缩方法一起使用，例如和albert还有DistilBert等联合使用，效果也还不错，感兴趣的同学可以进一步验证。

小结

本次解读的论文主要通过分析transformer中注意力头之间的冗余信息，并设计了一种优化后的多注意力头整合方法，将通用的信息提取出来共享于所有注意力头，让每个注意力头可以专注于捕捉独有的信息。此方法经过验证，可以在提升性能的同时只会损失极小的精度。另外，本论文还提出对预训练的bert模型中的attention权重进行张量分解，使得本文的多注意力头整合方法同样可以适用于预训练模型，拓展了本方法的适用范围，个人认为该方法值得在实际业务中进行尝试。

由于本人的数学功底不深，因此对于张量分解这块内容的解读比较浅，还有很多问题亟待解答，例如是不是可以通过其他分解方式更高效得去分解bert模型权重？这个就需要感兴趣的同学继续深入探索了。

添加个人微信，备注： 昵称-学校（公司）-方向 ， 即可获得

1. 快速学习深度学习五件套资料

2. 进入高手如云DL&NLP交流群

记得备注呦