NP完备破解羊了个羊？

会员服务 ·

NP完备破解羊了个羊？

2022 年 10 月 10 日 新智元

新智元报道

作者：终军弱冠

编辑：QQ

【新智元导读】蹭热度的小游戏计算复杂性又来了~

近日，羊了个羊火遍了网络，一时间关于第二关怎样难、如何通关的文章也多了起来，但是从计算复杂性（computational complexity）的角度讨论游戏难度的文章应该还没有，所以这次我也写一篇关于计算复杂性的文章来碰瓷。

游戏的机制是比较简单的，简单说来就是地图上有一些不同类型的方块，玩家可以选择方块放入自己的槽位中（槽位有上限，是个常数），如果槽位中有三个相同类型的方块就消去，游戏目标是消去所有方块。游戏的难点在于地图上的方块是堆叠起来的，被叠在下方的方块不能被选择，只有在上方的方块被放入槽位后才能被选择（也就是解锁），有时被叠在下方的方块的类型都由于被遮挡而不可知。

事实上，羊了个羊与有些小游戏的机制很类似，而其中很多小游戏已经被证明是 NP-complete 的，所以我们比较确信也能证明推广了的羊了个羊是 NP-complete 的。这里我们给一个比较弱的、简单的归约构造，来说明推广的羊了个羊游戏是 NP-complete。这里我们说的推广是指方块类型的数量不限制于常数，被遮挡的方块类型是确定的且已知的，槽位数量固定为 3（槽位数量是其他常数也可以用类似方法，只要在游戏初期迫使玩家拿一个特殊类型的方块，而在游戏最后才能消去，整个过程中这个方块占用了一个槽位，相当于少了一个槽位）。当然，这里我们不考虑游戏道具的影响。

本文的归约主要抄袭的是 Computational Complexity of Games and Puzzles 网页上证明 Mah-Jongg 游戏（一个类似连连看的游戏，有的地方也叫麻将）是 NP-complete 的归约。

我们仍然使用 3-SAT 这个经典的 NP-complete 问题作为归约问题。我们对于 3-SAT 公式中的每个变量设置 3 个方块堆，一个方块堆用于模拟变量的赋值（TRUE or FALSE），一个方块堆对应于赋值为 FALSE，一个堆对应于赋值为 TRUE。模拟变量的赋值方块堆有两层，第一层是 4 个一样的对应于变量的方块，第二层包含变量被赋值为 TRUE 和 FALSE 的方块各一个以及填充方块。对应于赋值为 FALSE 的方块堆通常是多层的（也可能退化为一层），顶层包含两个对应于变量被赋值为 FALSE 的方块（用于配合之前赋值方块堆使用），下层包含对应于子句的方块（对应子句中变量以非的形式出现）以及填充方块。对应于赋值为 TRUE 的方块堆的结构是类似的。最后，还有一个用于验证解的方块堆，这个堆是多层结构，顶部包含了对应于子句的方块，中部是对应于变量的方块，底部是对应于子句的方块。

我们用一个具体的例子来描述这个归约，假设 3-SAT 的实例是

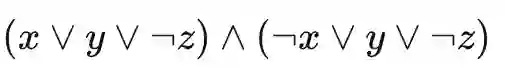。那么对于的羊了个羊游戏的实例如下（为了能表述每个方块的类型和堆叠情况，我们使用侧面视图的方式展示）

其中 C1 表示

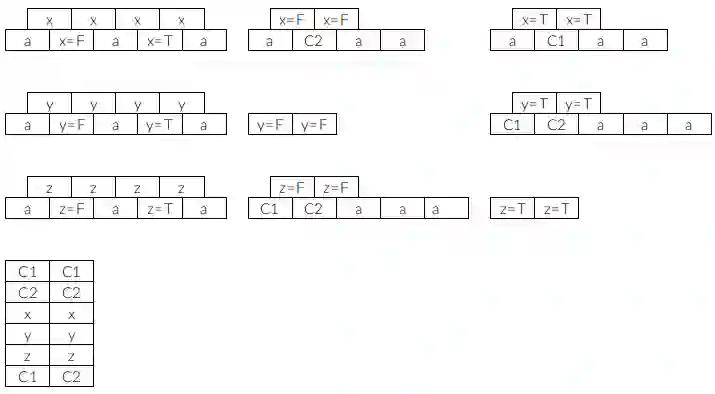
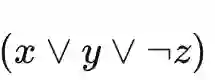，C2 表示

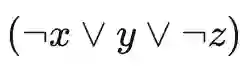，a 是填充方块，a 方块没有压住任何方块，所以可以留到最后再全部消去而不影响其他方块。注意这里我们设置的槽位数量是 3，也就是说选择某个方块放入槽里后就必须要消除这个类型的方块，否则就无法继续游戏了。

如果公式可满足，那么可以按照满足时各变量的赋值来消除方块。比如假设 xyz 全赋值为 FALSE，那么我们就对应消除最左侧的三个 x y 和 z，这样一来，第二层的方块 x=F y=F 和 z=F 就被解锁，我们就可以消去所有 x=F y=F z=F 方块，接着一个 C1 方块和两个 C2 方块就解锁，然后就能配合最下方的验证方块堆，消去验证堆的顶部两层，而后中间的变量 xyz 方块也马上能消去，最后就没有什么限制了，所有的方块都能够被消去。

反过来，如果所有方块可以消去（也就是该关卡可以通关），那么公式可满足。注意到验证堆中的变量 xyz 的方块想要被消去，必须上部的 C1 C2 子句方块都先消去，而子句方块又受限于赋值方块，赋值方块受限于变量方块，变量方块的摆放方式决定了在变量赋值时，每个变量只能赋为 FALSE 或 TRUE 中的一个（具体来说，在游戏初期 4 个 x 方块中任意消去 3 个后，方块 x=F 和 x=T 中必然有一个未被解锁）。这就意味着方块消去的顺序蕴含了一个满足公式的赋值。

这也就是说 3-SAT 公式可满足的充分必要条件是对应的羊了个羊游戏实例可通关。而羊了个羊显然属于 NP，因为能在多项式时间内判定一个操作序列是否能消去所有方块，从而我们就证明了下面的命题：

命题：在所有被遮挡的方块类型是确定且已知的条件下，推广的羊了个羊游戏属于 NP-complete。

用非人话来说就是，你没有办法设计一个多项式时间复杂度的算法来判断任意推广的羊了个羊关卡是否有解，除非 P=NP （这个只有 4 个字符的等式价值一个土地奖和 100 万美元，所以别去闲着没事就想着尝试证明或证否）。用人话来说就是，即使被遮挡的方块类型是确定的且已知的，计算机也仍然（几乎）无法快速地判断羊了个羊是否能通关。

参考资料：

https://zhuanlan.zhihu.com/p/567348731