243年前，欧拉的「未解之谜」被攻克：答案竟是量子力学！

2022 年 1 月 24 日 新智元

新智元报道

编辑：LRS

【新智元导读】243年前，欧拉留下著名的「三十六军官」谜题，至今仍然未得到完善的证明。最近量子物理学家表示他们解决了这个未解之谜，只不过要求军官是量子态的!

1779 年，瑞士大名鼎鼎的数学家莱昂哈德 · 欧拉（Leonhard Euler）曾提出一个问题：即从不同的 6 个军团（army regiment）各选 6 种不同军阶（rank）的 6 名军官（officers）共 36 人，排成一个 6 行 6 列的方队，使得各行各列的 6 名军官恰好来自不同的军团而且军阶各不相同，应如何排这个方队？

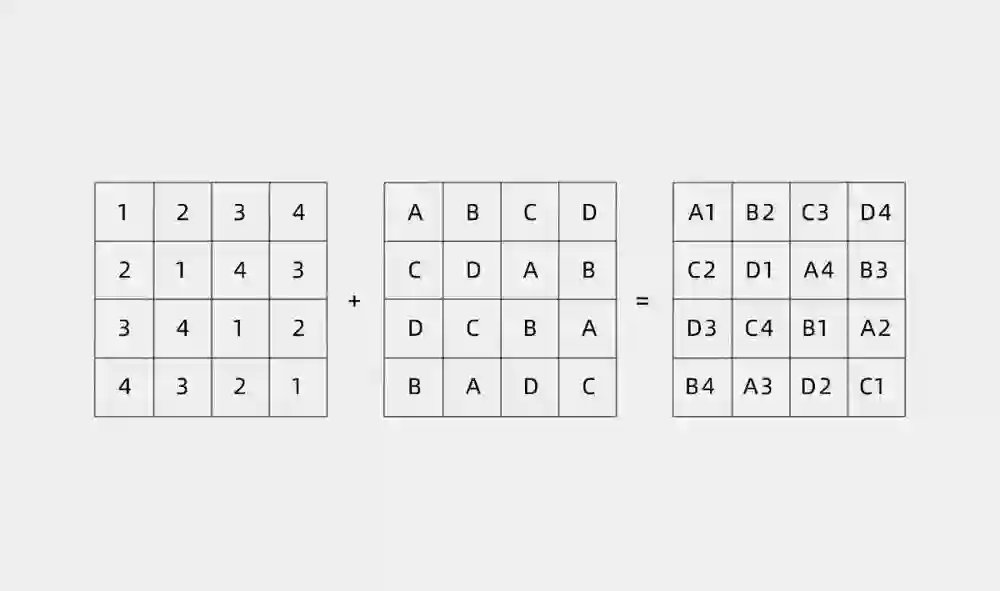
如果用(1，1)表示来自第一个军团具有第一种军阶的军官，用(1，2)表示来自第一个军团具有第二种军阶的军官，用(6，6)表示来自第六个军团具有第六种军阶的军官，则欧拉的问题就是如何将这36个数对排成方阵，使得每行每列的数无论从第一个数看还是从第二个数看，都恰好是由1、2、3、4、5、6组成。

这个问题史称为「三十六军官问题」，在很长一段时间都没有答案。

实际上当军阶和军团数为5或7时，这个难题就变得非常容易解决，唯独找不到三十六军官的解决方案。

于是在1782年，欧拉表示：在费尽心思求解之后，虽然无法给出严格的证明，但不得不承认这种排列（将36名军官以这种形式被排进6×6的方格中）是不可能的。

当时，欧拉证明了对于这个谜题来说，任何不是以4k+2的形式存在的军团数和军阶，都存在解。他表示，他所采用的证明方法不适用于对这种形式的数字进行证明。

直到一个多世纪后的 1901 年，法国数学家加斯顿 · 塔里（Gaston Tarry）证明，确实没有办法将欧拉的 36 名军官排列在一个 6×6 的正方形中而不重复，他写出了 6x6 正方形的所有可能排列，证明 36 个军官问题是不可能的。

时间转眼到了1960年，数学家借助计算机这个大杀器，数学家们证明：这个谜题对于任何大于2的军团数和军阶数都存在解，唯独除了6。

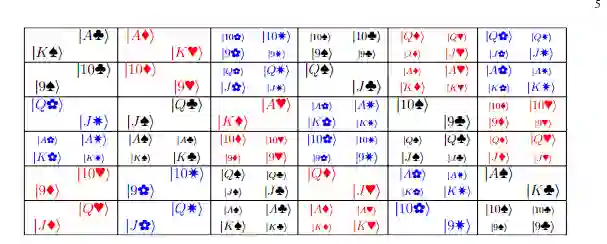
例如下图中就展示了一个5×5的方阵，可以用5种不同等级和5种不同颜色的棋子填充，且在同一行或同一列不会存在重复的等级或颜色。

时间到了 1960 年，数学家们使用计算机证明了对于任何数量的军阶和军团问题，都有解决方案，除了 6 个军阶和 6 个军团。

遇事不决，量子力学

三十六军官问题和「数独」游戏看起来十分相似，但在数学上对这两类puzzle还有一个分类。

数独是一种「拉丁方阵」，即方阵是一种由符号（数字和字母）构成的方阵，其中每个符号在每一行和每一列中只出现一次。如果将两个有着相同的大小但不同的符号的拉丁方阵组合在一起，就会得到一个希腊拉丁方阵，也称为欧拉方阵，主要特点就是包含成对的符号。

所以如果三十六军官问题的解存在，那一定会是一个6x6的希腊拉丁方阵，成对的属性为军阶和军团。

最近，《物理评论快报》上的一篇论文，来自印度理工学院（马德拉斯理工学院校区）、雅盖隆大学等机构的量子物理学家证明，采用量子力学的思路，就能够以符合欧拉标准的方式把这36 名「量子版的军官」安排到格子里。

论文地址：https://arxiv.org/abs/2104.05122

在经典版本中，方阵中的每个格子都代表着一个有着明确军阶和军团的军官。

但在量子力学版本中，像电子这样的粒子可以处于多种可能状态的「叠加态」，量子版的军官是由它的军阶和军团的叠加构成的。例如，一个军官可以是红色的王和橙色的后的叠加。

最关键的是，组成了这些军官的量子态存在纠缠关系。例如一个红色的王与一个橙色的后纠缠在一起，那么即使这个王和后同时处于多个军团的叠加态，测量到王是红色就能得知后是橙色。由于这种特殊的纠缠属性，每一行或每一列上的军官都可以是相互垂直的。

为了证明这种理论，研究人员需要构建一个被这些量子军官填满的6×6的方阵。由于存在大量的可能组合以及纠缠，因此他们必须借助量子计算机。

在方阵中，研究人员先要输入一个这个谜题的经典版本的近似解。在这个近似解中，36个经典军官的排列在一行或一列中只存在少量的军阶和军团重复。

接着，他们对这个解应用了一种能将这种排列调整为真正的量子解的算法。这个算法的工作原理有点像用蛮力解魔方——先固定第一行，然后固定第一列、第二列……当他们一遍又一遍地重复这个算法时，就可以越来越接近真正的解。

利用这种算法，他们最终得到了36军官谜团的真正的解。在某种意义上，证明了欧拉对于36军官谜题的判断是「错误」的。

不过可以肯定的是，18世纪的欧拉是不可能想到军官还能「量子化」的。

值得一提的是，新的解有一个特点，那就是军官的军阶只与相邻等级纠缠，比如王与后、车与象、马与兵，而军团也只与相邻的兵团纠缠。并且在量子拉丁方格中的系数比率也是1.618，即著名的黄金比例。

当然了，243年来数学家并不是只在追求一个puzzle的答案，该解决方案也被称为绝对最大纠缠态 (AME，Absolutely Maximally Entangled state)，能够解决关于量子对象的排列问题，在包括量子纠错在内的许多应用都很重要，例如提供一种在量子计算机中存储冗余信息的方式，这样即使数据损坏，信息也能保存下来。

在 AME 中，量子对象的测量值也存在比较强的相关性。

以抛硬币来说，如果两个人（A、B）抛纠缠硬币，其中 A 抛硬币并得到正面，那么他定肯知道 Bob 是反面，反之亦然。两枚硬币可以最大限度地纠缠在一起，三枚也可以，但四枚不行：如果有两个人一起加入抛硬币，A 就永远不知道 B 得到了什么。