魔改CNN揭秘宇宙大爆炸：物理学的核心是对称性

博雯 发自 凹非寺
量子位 | 公众号 QbitAI

宇宙大爆炸刚刚发生的那几秒是什么样的？

这可以说是物理学领域中最复杂的问题之一了，就以大爆炸刚刚发生的几百万分之一秒内，宇宙的一种特殊的存在形态为例。

这是一种超高温下的“完美液态”，对探索宇宙本源物质的结构和环境有着及其重大的意义。

在实验室中，必须要在15万倍太阳中心温度的严苛环境下才能成功模拟这一形态。

要对这这种高度复杂的物理学形态进行分析或处理，超级计算机需要极长的时间逼近其形态，经典的AI或CNN也很难基于其中的物理学概念作出有意义的解释。

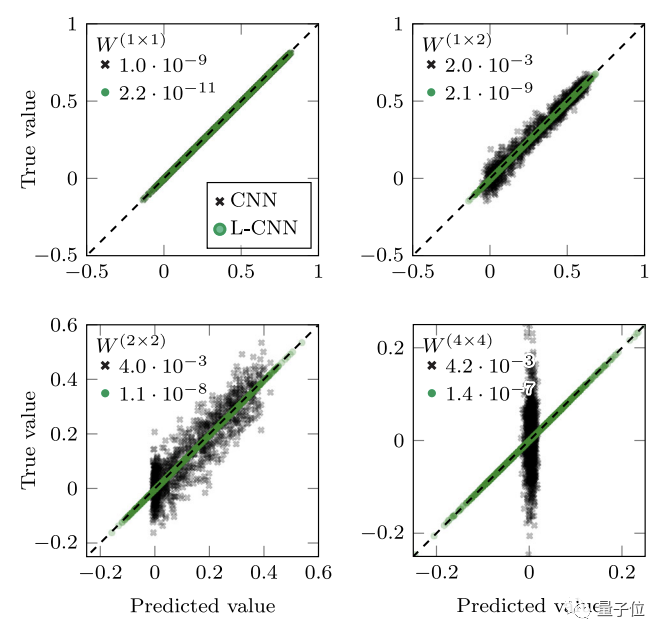
但现在，物理学顶刊PRL上的一篇论文提出了一种叫做L-CNN的新型神经网络结构，很好地解决了上面的问题：

如何处理规范不变量

在我们深入了解L-CNN的结构之前，先来明确一个事实：

传统AI和CNN做不到的任务到底是什么？

以开头提到的“完美液态”为例，这种形态是指在极高能量和温度下，质子和中子被拆解，并重新结合成一种叫做夸克胶子等离子体（QGP）的新型物质形态。

（最初物质形成之前的整个宇宙都是这种形态）

当引入AI对QGP形态进行分析和解构时，就必须要考虑其规范对称性 （Gauge Symmetry）。

规范对称性是指用不同方法描述同一件事件，比如，我们可以用一对相位和电磁场势描述一个电子-光子系统，也可以用另外一对来描述，这两个描述应该给出同一个物理实质。

而物理量都是规范不变的，因此，看上去用不同的数学方式描述的粒子场及其相互作用力，或许实际上就是相同的物理状态。

传统CNN很难计算或分析这些规范不变量，自然就无法得到有意义的计算机模拟结果。

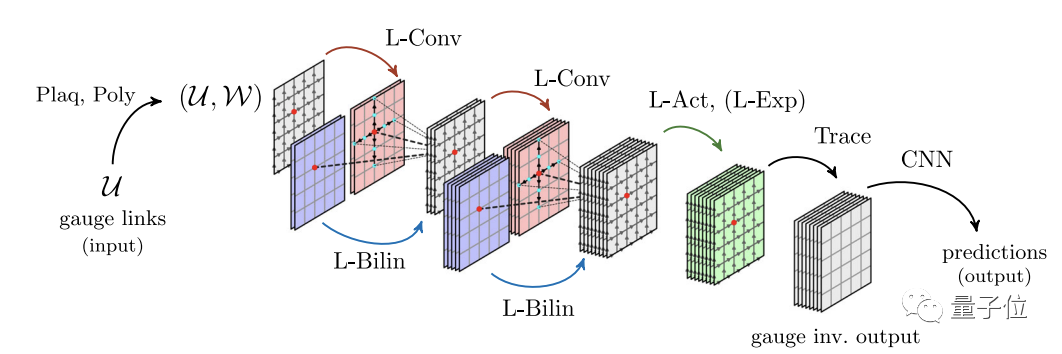
而开头提到的新方法L-CNN全名格点规范等变（Lattice Gauge Equivariant）神经网络，是一种全新的，可以对传统CNN无法处理的规范不变量进行计算或分析的方法。

整个方法是基于格点规范场论 （Lattice gauge theory）实现的。

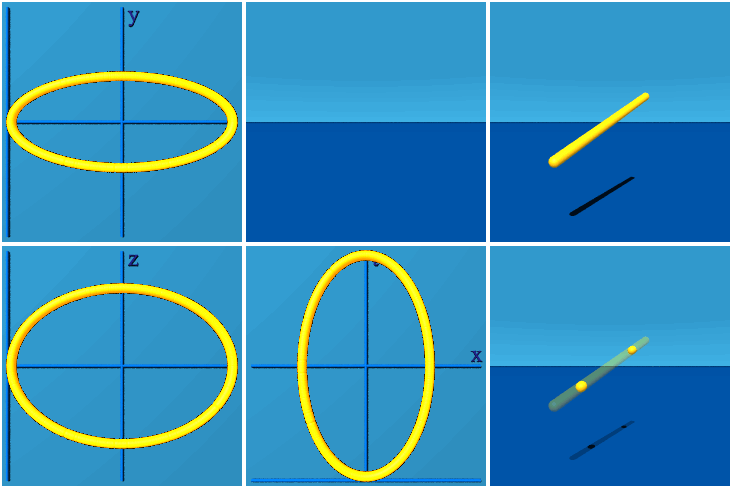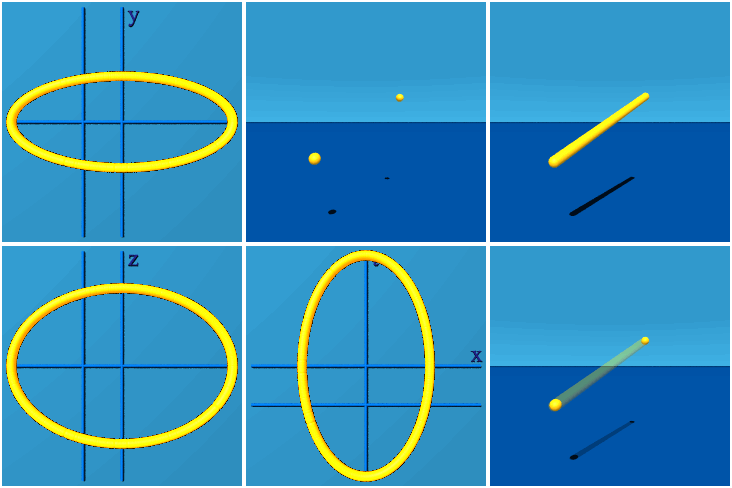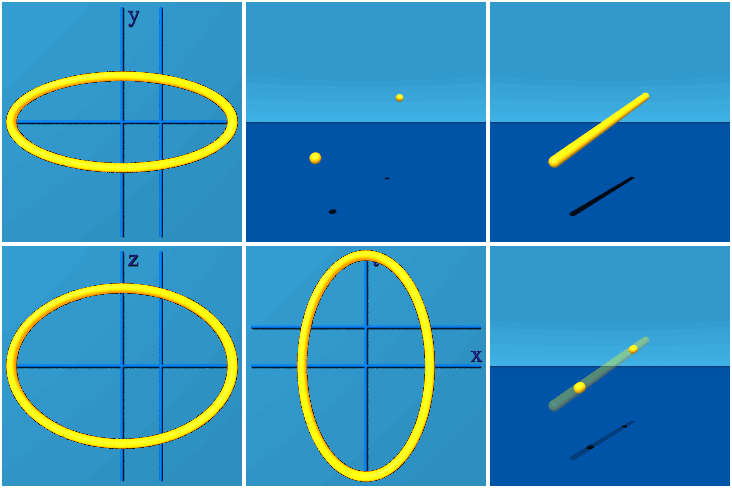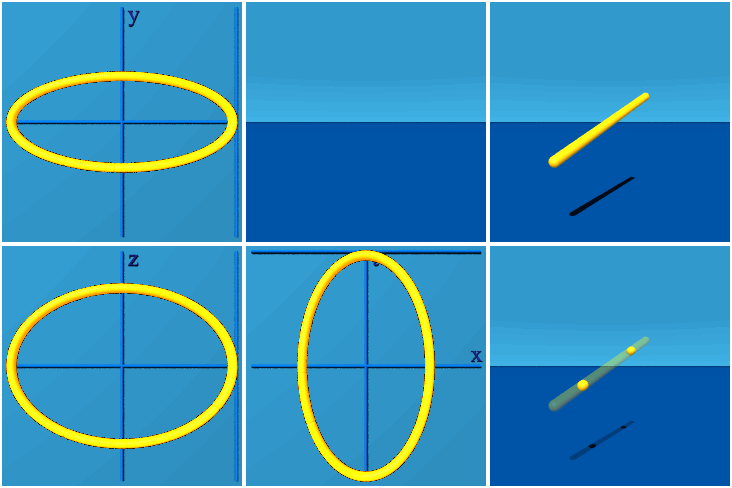
在格点上，规范不变量通常是以不同形状的威尔逊环 （Wilson Loop）来进行描述。

具体的，加入一个新的卷积层，能在连续的双线性层中形成任意形状的威尔逊环，同时保留规范等价性（Gauge Equivariance）。

而所有可收缩的威尔逊环的集合都可以通过上述方法生成，再加上来自非收缩环路的拓扑信息，原则上就可以重构所有的规范连接。

有了这样的神经网络，就有可能对多个物理学的复杂系统进行预测。

论文作者Andreas Ipp还用夸克胶子等离子体举了个例子：

比如，L-CNN不用详细计算每一个中间步骤，就能估计夸克胶子等离子体在以后某个时间点的样子。

同时，它也能确保系统只产生与规范对称不矛盾的结果，也就是至少在原则上有意义的结果。

这是以前所有的计算方法都很难做到的，L-CNN无疑为模拟复杂物理现象提供了一种新思路。

未来，它还会为探索生命体最初瞬间存在的环境、理解宇宙中物质的本源状态，以及黑洞、大统一理论的研究提供更多的帮助。

作者介绍

论文共有四位作者，都来自维也纳科技大学（TU Wien）的理论物理研究所。

其中右下角为论文的通讯作者David I. Müller，为维也纳科技大学理论物理研究所的博士后，主要研究领域为高能物理学、格点规范场、机器学习。

论文：
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.032003

参考链接：
https://www.eurekalert.org/news-releases/941106

— 完 —

「智能汽车」交流群招募中！

欢迎关注智能汽车、自动驾驶的小伙伴们加入社群，与行业大咖交流、切磋，不错过智能汽车行业发展&技术进展。

ps.加好友请务必备注您的姓名-公司-职位哦~

点这里👇关注我，记得标星哦～

一键三连「分享」、「点赞」和「在看」

科技前沿进展日日相见~