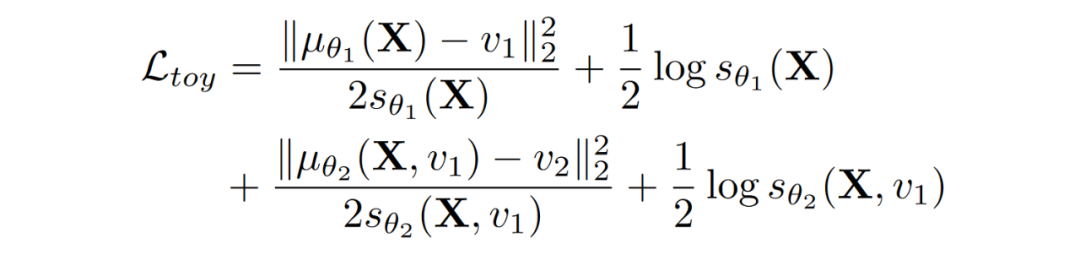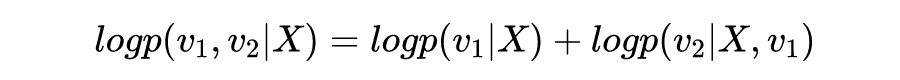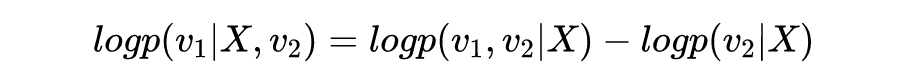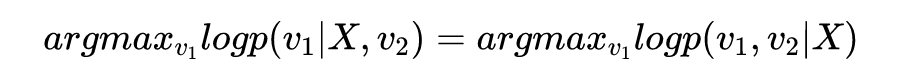从Bayesian Deep Learning到Adversarial Robustness新范式

2021 年 12 月 29 日 PaperWeekly

©作者 | 王灏、毛成志

单位 | Rutgers University / Columbia University

研究方向 | 贝叶斯深度学习 / 对抗鲁棒性

拖延症赶在 2021 结束前来介绍一下我们 ICCV 2021 上基于 Bayesian Deep Learning [4,5]（或者更具体是 Deep Bayesian Network）做 Adversarial Robustness 的 work [1]。

论文标题：

Adversarial Attacks are Reversible with Natural Supervision

论文链接：

http://wanghao.in/paper/ICCV21_ReverseAttack.pdf

代码链接：

https://github.com/cvlab-columbia/SelfSupDefense

视频链接：

https://www.youtube.com/watch?v=0Yv3eQ9JR4Y

Adversarial Robustness 新思路：可以说，这个 work 提出了一个 adversarial defense 的新范式，叫做 Reverse Attack。举个简单的例子，如下图，给定一个原始图片（下面左边的图），attacker 会通过比如 PGD 的方法，找到一个 attack vector（下面中间的图），叠加在原始图片上，而我们 reverse attack 的思路是，在 inference time（或者叫 test time）临时找到一个 reverse attack vector（下面右边的图），再次叠加在已经被 attack 过的图片上，从而来抵消掉部分 attack vector。

把 Reverse Attack 作为 Bayesian Inference 来解： 那么问题来了，defense 方拿到的图片已经是被 attack 过的（已经叠加了 attack vector），那我们如何能机智地找到一个有效的 reverse attack vector 呢？这就要回到文章的开头，Bayesian Deep Learning 和 Deep Bayesian Network 了。简单地讲，我们把寻找 reverse attack vector 作为一个 Bayesian inference 的问题来解。假设被 attack 过的图片（原始图片+ attack vector）叫 , 而我们想寻找的 reverse attack 后的图片（原始图片+ attack vector+reverse attack vector）叫，那么寻找 reverse attack vector 的过程其实可以 formulate 成：

求一个，使得后验概率最大。

这里的表示的是图片的结构一致性信息（具体的讲，就是同一图片的不同部分的颜色、纹理、内容应该一致），而这个信息是已知的，因为不管图片有没有被 attack 过，我们都知道，我们需要还原的图片，它肯定是满足结构的一致性的。关于的问题我们下文会再仔细讨论。

最大后验估计和 Deep Bayesian Network： 那么现在的主要问题是，如何有效，而且 robust 地得到的最大后验呢？答案就是可以基于我们之前在 AAAI 2019 提的一个 Deep Bayesian Network（深度贝叶斯网络） [2] ，叫做 Bidirectional Inference Network（BIN）。

论文标题：

Bidirectional Inference Networks: A Class of Deep Bayesian Networks for Health Profiling

论文链接：

http://wanghao.in/paper/AAAI19_BIN.pdf

代码链接：

https://github.com/js05212/bidirectional-inference-network

下面我们先简单介绍一下 BIN，然后再回过头来介绍如何把 BIN 的思想用到 Reverse Attack 上。

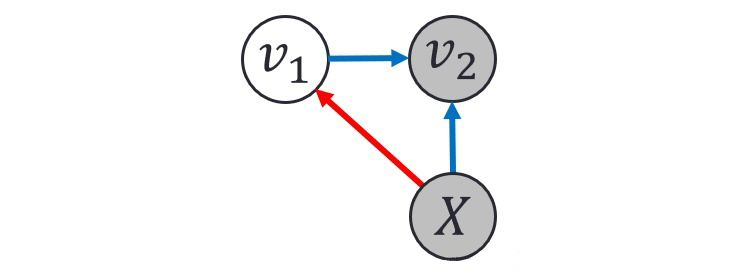
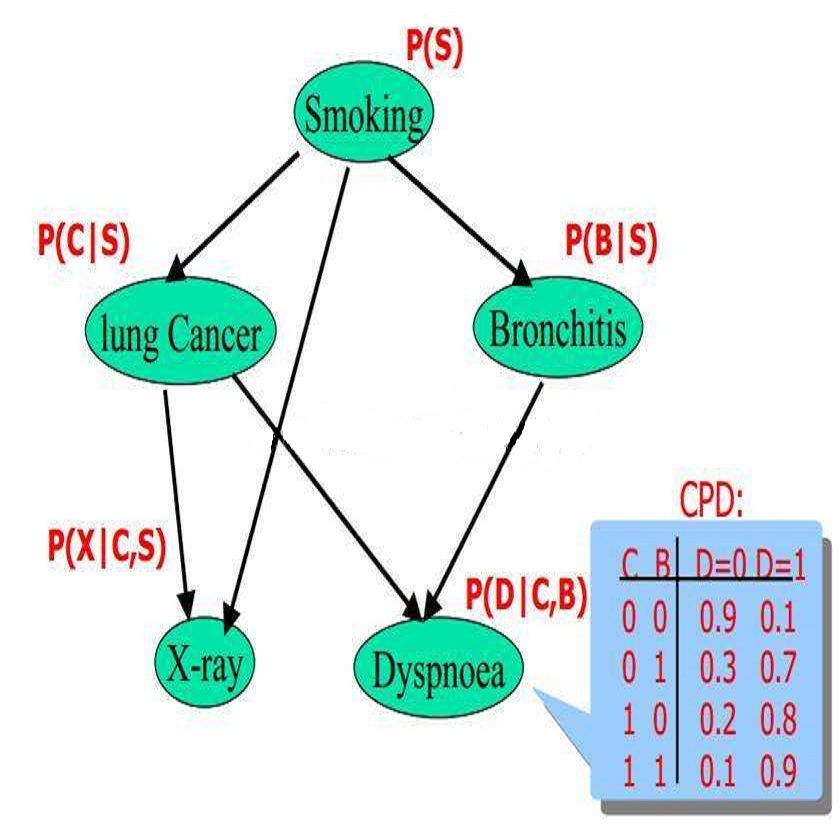
BIN属于Deep Bayesian Network，那么什么是Bayesian Network（贝叶斯网络）呢？

贝叶斯网络： 比如下图就是一个贝叶斯网络。

图里面 4 个节点分别表示四个随机变量，，。而图里的边则表示的是 conditional dependency。到的边表示，而和同时指向的边表示。灰色的节点表示已知的值（observed variable），而白色的节点表示我们需要推断的值（latent variable）。正如神经网络，贝叶斯网络也分成学习（learning）和推断（inference）两个阶段。

贝叶斯网络的学习： 一般贝叶斯网络的学习指的就是通过数据，学习到各个条件概率分布。比如上面的图，如果我们有很多和对应的数据，我们就可以学到这个条件概率分布。同理如果我们有很多、和的数据，我们也可以学到。

贝叶斯网络的推断： 在模型学习后，我们会根据已经学到的各个条件概率分布，来做概率推断，比如，虽然我们在学习阶段只学到了和两个个条件概率分布，但是根据 Bayes Rule 我们可以做更多的推断任务，比如给定和，我们可以推断出最可能的值是多少；正式地讲，我们可以找到一个的值，从而使得最大。而找这个值的过程就是最大后验推断。（贝叶斯网络的推断是一个非常广泛的问题，有兴趣的同学可以参考相关的教科书，我们这里只是简要介绍一些这个文章需要用到的部分。）

从贝叶斯网络到深度贝叶斯网络： 那么现在的问题是，如果和这两个条件概率分布非常复杂，每个都需要用多层的神经网络来表示，那该怎么办？我们该如何学习（learning），如何推断（inference）呢？

深度贝叶斯网络的学习： 学习的部分其实很简单，假设我们有很多，，的数据，我们只需要分别训练 2 个概率神经网络（Probabilistic Neural Network），一个负责，一个负责。这里的概率神经网络和一般的神经网络不同的是：概率神经网络会输出整个分布的参数，而一般的神经网络只会输出一个预测的定值。最简单的概率神经网络的做法是，我们假设网络输出的是高斯分布，那么我们就可以用高斯分布 log likelihood 作为目标函数，来训练（学习）和这两个概率神经网络。整体地看，我们可以用下面这个目标函数来训练：

这个目标函数的前 2 项对应的是这个概率神经网络，这个网络的输入是，而这里的和则分别是这个概率神经网络输出的 mean 和 variance。所以，前 2 项其实是在用一个被控制的高斯分布，来拟合。注意这里表示第一个神经网络的参数。

同理，目标函数的后 2 项对应的是这个概率神经网络。有了这个目标函数以及很多，，的数据，我们就可以训练出来和这两个概率神经网络。（眼尖的同学可能会发现，前 2 项和后 2 项是没有关系的，所以这 2 个网络还可以分开、并行地训练，从而提高速度。）

深度贝叶斯网络的推断： 深度贝叶斯网络的推断部分是 BIN 的精髓，也是 Reverse Attack 的灵感来源之一。我们依然沿用前面，，的例子，在我们学习了和这两个概率神经网络之后，一个重要的推断问题是，如果给定一组和，我们能否推断出最可能发生的。换句话说，我们能否找到一个，使得的后验概率最大呢？

熟悉概率论的人可能已经发现上面的目标函数，其实等于：

而后验概率的 log：

由于我们和是给定的，所以上面的第二项其实是一个常数，那么我们就可以推出来：

然后我们会惊喜地发现（这其实是最大后验的常规操作），其实给定和推断的时候，我们可以用同一个目标函数：

区别在于，在学习（learning）阶段，我们是已知，，，然后通过 BP 去更新网络的参数和。而在推断（inference）阶段，我们是已知，，和网络的参数与，然后通过 BP 去更新 。

眼尖的同学可能会发现另一个区别，那就是在学习阶段，前 2 项和后 2 项是独立的、没有关系的，但是在推断阶段，我们的推断目标 同时出现在前 2 项和后 2 项里。也就是说，虽然 2 个概率神经网络可以分开训练，但是推断的时候是需要一起协作的。

深度贝叶斯网络推断的 intuition：其实如果只看后面 2 项，可以发现，我们做的其实就是 BP 到神经网络的输入，从而不断更新，而前面 2 项的作用，其实相当于给这个更新提供了一个 L2 的 regularization。而这个 L2 regularization 的系数，则由动态决定的。

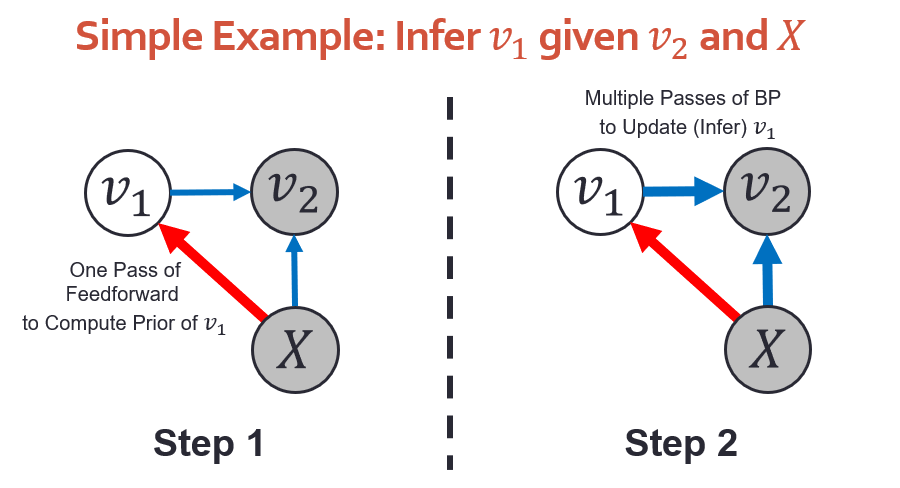
算法实现： 从算法上讲，这个推断过程可以分成 2 步（如下图）：（1）计算上面目标函数的前 2 项里的和，这个部分只需要通过 feedforward 计算一次，（2）把 初始化为，然后通过 BP 多次计算目标函数关于的 gradient，并且更新。

因为我们这个方法既可以前向推断（feedforward）也可以后向推断（BP），我们把它叫做 Bidirectional Inference Network（BIN）。

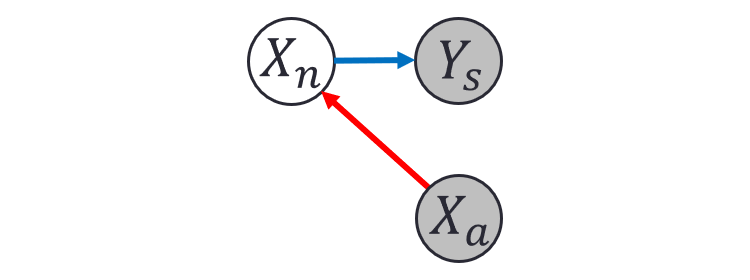
从 BIN 到 Reverse Attack： 那么回到文章最初提的 Reverse Attack，假设被 attack 过的图片（原始图片+ attack vector）叫，而我们想寻找的 reverse attack 后的图片（原始图片+ attack vector+reverse attack vector）叫。这里的关键是结构一致性信息。我们知道，原始的图片，是满足结构一致性的（），而被 attack 后的图片，结构一致性会被破坏（或者甚至），然后我们希望 reverse attack 后的图片，可以（部分）恢复这种结构一致性（使得 尽可能靠近 1 ）。

那么我们应该怎么做呢？这时我们就可以把它 formulate 成一个最大后验估计的问题：寻找一个使得后验概率最大。套用前面 BIN 的例子，这里的对应之前的，对应之前，而对应之前的。于是我们就有了下面这个熟悉的图。需要注意的是，在 reverse attack 里问题甚至比之前的例子更简单，因为和之间没有链接。

Reverse Attack 与 BIN的推断： 给定一个 reverse attack 后的图片，以及已知我们 reverse attack 后的结构一致性，根据 BIN 的推断（inference）算法，我们只需要通过 BP，来求关于的 gradient，然后不断更新到收敛，就可以找到最优的了。

如何学习概率神经网络和： 细心的读者会问，BIN 的 inference 是假设已经学好了概率神经网络和，那么如何学习这两个概率神经网络呢？

其实很简单，甚至不需要学习，我们直接假设服从一个以为均值的高斯分布就行。

至于，我们可以直接训练一个 contrastive learning（CL）的神经网络。给定任意 2 个图片的 crop 作为输入，CL 的网络可以判断他们是否来自于同一张图。这其实就是在判断结构一致性。被 attack 过的图片，结构一致性受损（），所以即使给定这同一个图片的 2 个 crop，CL 的网络也可以判断出来他们不是来自于同一张图（）。基于这个 intuition，我们只需要直接用 clean image，训练一个 CL 的网络，就可以当成来用了。

理论： 更有趣的是，在我们 reverse attack for defense 的 paper 中，我们还证明了，通过以上贝叶斯推断得到的模型准确率的上界可以提升。也就是说，从某种程度上讲，用了这种基于贝叶斯的 reversal method，对于训练恰当的模型会保证更好。

实验结果： 因为我们的方法只是在原有输入的基础上额外考虑了这一项，因此我们的算法与目前所有做 adversarial robustness 的方法兼容，可以直接加到他们上面。我们在 4 个主流的数据集上，对7种主流的 adversarial robust 的算法进行了测试。

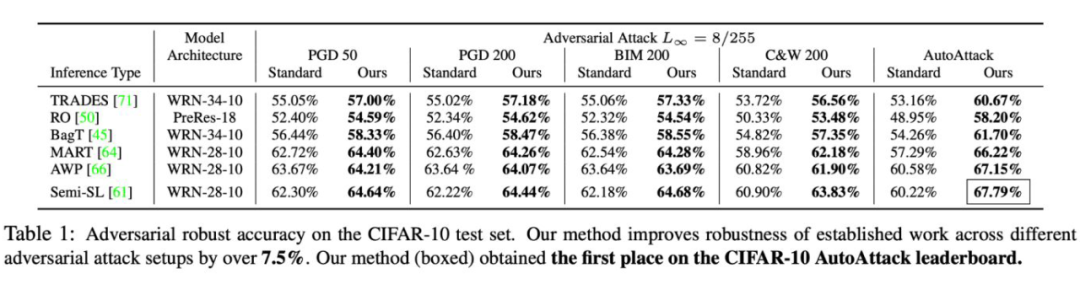
实验结果之 CIFAR-10： 我们测试了 6 种主流 adversarial robust 算法，并且在他们上面加入我们 reversal defense 的方法。在包括 AutoAttack 在内的 5 种 adversarial attack 下，我们的算法都直接提升了原有算法的 robust accracy。

有意思的是，对于越强的 adversarial attack 算法，我们的算法提升的越多（对于比较弱的 PGD50，我们提升 2% 左右，但是对于更强的 autoattack，我们能够提升 7 个点之多）。这是因为更强的 attack 算法其实破坏了更多的结构一致性信息，我们的算法从而能够恢复更多原有信息来提升准确率。

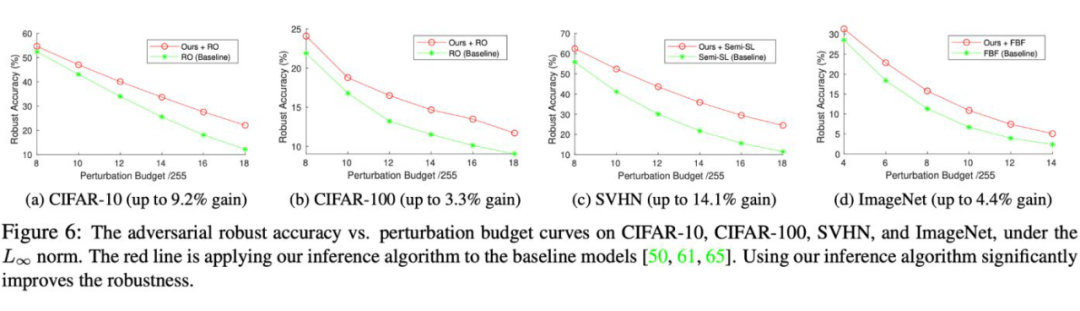
实验结果之 CIFAR-100，SVHN 和 ImageNet： 我们的算法同样可以扩展到更大规模的数据集。在另外 3 个数据集上，我们的算法同样有高达 11% 的提升。下面是每个数据集的结果：

另一个使用贝叶斯最大后验来增强鲁棒性的优点 ，就是我们的方法对于没见过的，特别强的 adversarial attack 更加有效。在以下图中，所有的模型都在最小的扰动上进行训练（使用 8/255 的扰动范围，ImageNet 除外，是 4/255）。随着在推断时扰动的增加，我们的模型在这些从未训练过的扰动上准确率提升越来越明显。

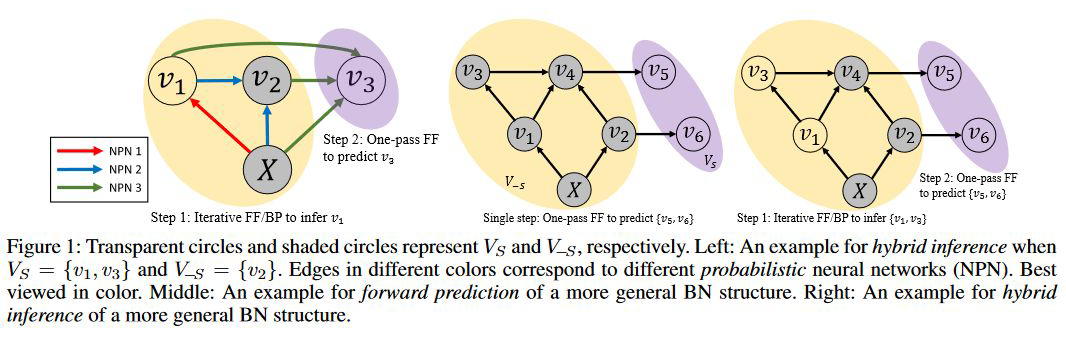
写在最后之用 BIN 处理任意贝叶斯网络结构： 有一点需要注意的是，虽然我们上面给的是一个非常简单的深度贝叶斯网络结构，只涉及 3 个变量。实际上 BIN 可以处理任意节点数的贝叶斯网络，比如下图这些结构。因为可以处理任意结构， BIN 最初是用来做 health profiling 的。有兴趣同学可以移步看看 health profiling 通俗易懂的应用介绍：

https://news.mit.edu/2019/machine-learning-incomplete-patient-data-0125

写在最后之用 natural-parameter network（NPN）来作为 BIN 的概率神经网络 backbone： 另一点需要注意的是，上文提到的概率神经网络（probabilistic neural network）的具体实现（比如的具体实现），除了简单的用一个 MLP 最后输出 2 个 branch（mean 和 variance）之外，也可以用比如 natural-parameter network（NPN） [3] 的贝叶斯神经网络，从而达到更好的效果。

这一篇的数学公式稍微有点多，由于篇幅限制，也省去了一些技术细节，如果有啥编辑或者逻辑不顺，大家轻拍：）大家有兴趣的话也欢迎找 @ChengZhi（Reverse Attack的一作） @何昊或者我讨论。

参考文献

[1] Adversarial attacks are reversible with natural supervision. Chengzhi Mao, Mia Chiquier, Hao Wang, Junfeng Yang, Carl Vondrick. ICCV, 2021.

[2] Bidirectional inference networks: A class of deep Bayesian networks for health profiling. Hao Wang, Chengzhi Mao, Hao He, Mingmin Zhao, Tommi S. Jaakkola, Dina Katabi. AAAI , 2019.

[3] Natural parameter networks: a class of probabilistic neural networks. Hao Wang, Xingjian Shi, Dit-Yan Yeung. NIPS, 2016.

[4] A survey on Bayesian deep learning. Hao Wang, Dit-Yan Yeung. ACM Computing Surveys, 2020.

[5] Towards Bayesian deep learning: a framework and some existing methods. Hao Wang, Dit-Yan Yeung. TKDE, 2016.

更多阅读