【GNN】VGAE：利用变分自编码器完成图重构

今天学习的是 Thomas N. Kipf 的 2016 年的工作《Variational Graph Auto-Encoders》，目前引用量为 260 多。

VGAE 属于图自编码器，是图神经网络细分类别的一大类。Kipf 同学也非常厉害，其影响力最大的一篇论文莫过于 2017 年提出的 GCN 模型。

VGAE 全称为 Variational Graph Auto-Encoders，翻译过来就是变分图自编码器，从名字中我们也可以看出 VGAE 是应用于图上的变分自编码器，是一种无监督学习框架。

看到这可能不知道大家都没有疑问，至少我会有以下几点疑问：

1. 自编码器是利用编码与解码对数据进行压缩，加上变分后的 VGAE 是什么？
2. 自编码器是通过隐藏层节点数小于输入层节点数实现数据压缩，VGAE 如何实现？
3. 自编码器预测的目标是输入，而 VGAE 要预测的是什么？

1.Introduction

我们知道自编码器的是通过减少隐藏层神经元个数来实现重构样本，自编码器为了尽可能复现输入数据，其隐藏层必须捕捉输入数据的重要特征，从而找到能够代表原数据的主要成分。

变分图自编码器也具有类似的目的，其主要是为图中节点找寻合适的 Embedding 向量，并通过 Embedding 向量实现图重构。其中获取到的节点 Embedding 可以用于支撑下游任务。

2.VGAE

2.1 VAE

在介绍 VGAE 之前，我们先介绍下 VAE（Variational Auto-Encoders）。VAE 了解清楚后，VGAE 也算完成了 80%。

VAE 最早来源于 2014 年 Kingma 的一篇论文《Auto-Encoding Variational Bayes》。该论文目前引用数超 8300 次，作者 Kingma 和 Kipf 都来自于阿姆斯特丹大学。

VAE 是变分贝叶斯（Variational Bayesian）和神经网络的结合。

简单介绍下变分贝叶斯方法：我们知道统计模型由观察变量 x、未知参数 和隐变量 z 组成，生成模型是通过隐变量来估计观察变量： 。但很多情况下，这个后验概率并容易得到（因变量和参数都不知道），所以我们就需要通过其他的方式来近似估计这个后验概率。贝叶斯统计学传统的推断方法是采用马氏链蒙特卡洛（MCMC）采样方法，通过抽取大量样本给出后验分布的数值近似，但这种方法的计算代价昂贵。而变分贝叶斯是把原本的统计推断问题转换成优化问题（两个分布的距离），并利用一种分析方法来近似隐变量的后验分布，从而达到原本统计推断的问题。

而 VAE 则是利用神经网络学习来学习变分推导的参数，从而得到后验推理的似然估计。下图实线代表贝叶斯推断统计的生成模型 ，虚线代表变分近似 。

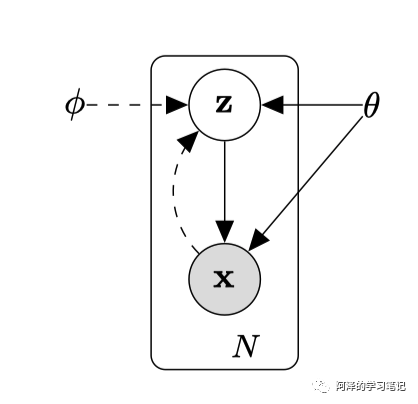
这篇论文里最重要的就是公式，为了简单起见，不进行公示推导。直接说结论：作者提出了 AEVB（Auto-Encoding Variational Bayesian）算法来让 近似 ，同时把最大似然函数的下界作为目标函数，从而避开了后验概率的计算，并且将问题转换为最优化问题，同时可以利用随机梯度下降来进行参数优化。

VAE 模型中，我们假设 这个后验分布服从正态分布，并且对于不同样本来说都是独立的，即样本的后验分布是独立同分布的。可能大家会有个疑问：

1. 为什么是服从正态分布？
2. 为什么要强调是各样本分布是独立的？

对于第一个问题，这里只是做一个假设，只要是一个神经网络可以学到的分布即可，只是服从正态分布就是 VAE 算法，如果服从其他的分布就是其他的算法；

对于第二个问题，如果我们学到的各变量的分布都是一致的，如：

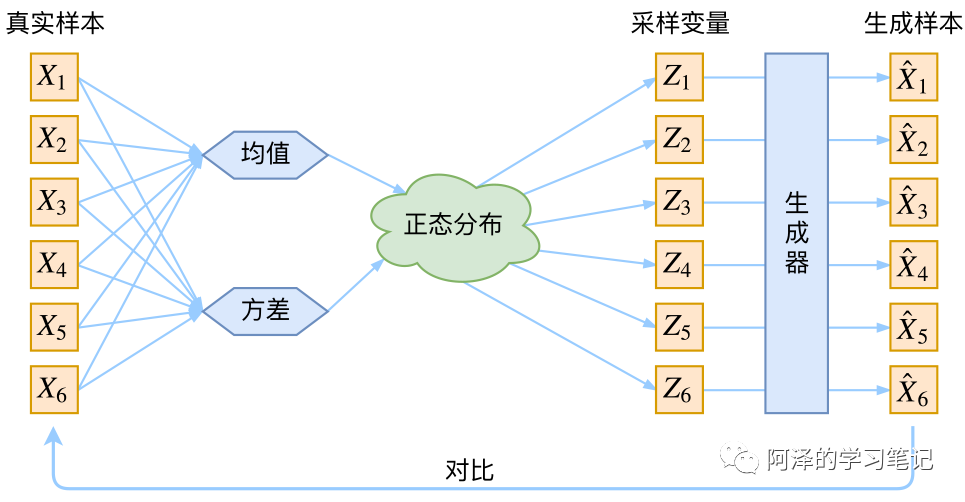
这样的结构无法保证通过学到的分布进行采样得到的隐变量 能够与真实样本 一一对应，所以就无法保证学习效果了。

所以 VAE 的每个样本都有自己的专属正态分布：

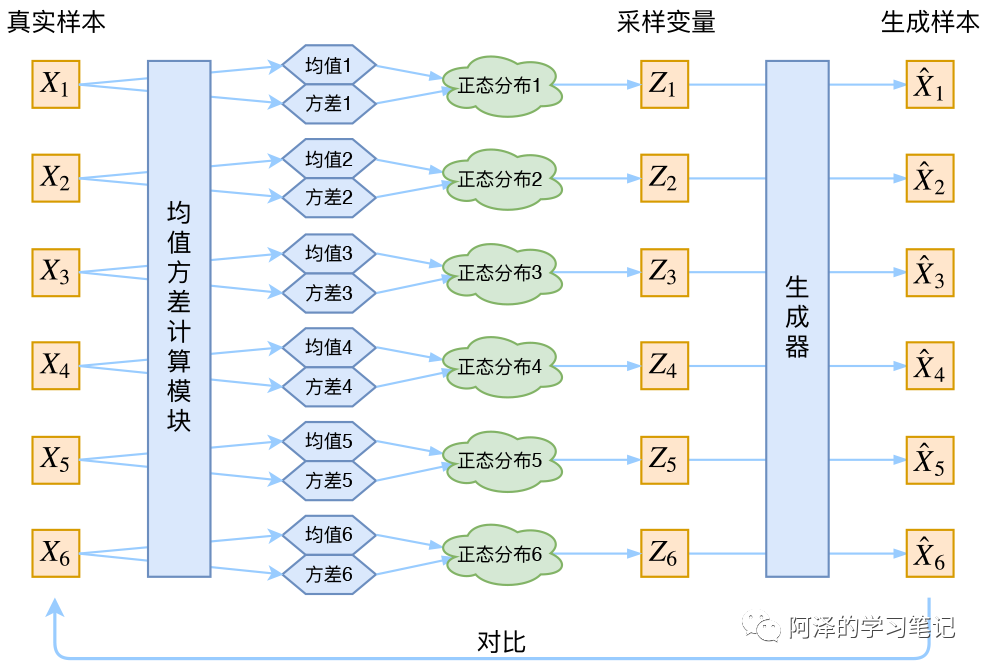
这样，我们便能通过每个样本的专属分布来还原出真实样本。

这也是论文中最重要的一点：

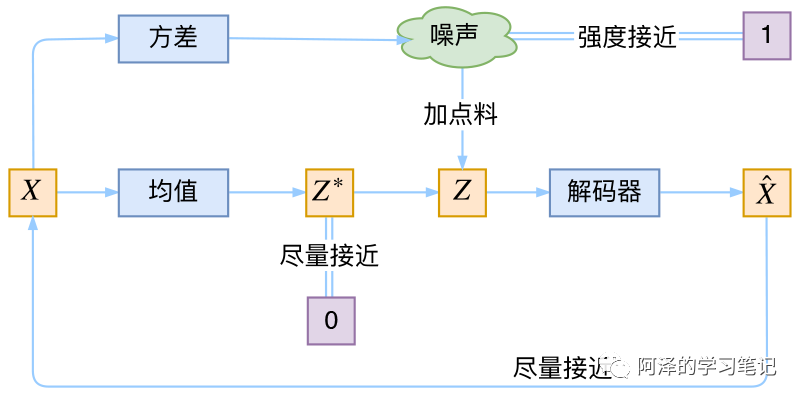
VAE 通过构建两个神经网络来分别学习均值和方差 ，这样我们便能得到样本 的专属均值和方差了，然后从专属分布中采样出 ，然后通过生成器得到 ，并通过最小化重构误差来进行约束 。

但隐变量是通过采样得到的，而不是经过编码器算出来的。这样的重构过程中免不了受到噪声的影响，噪声会增加重构的难度，不过好在这个噪声的强度可以通过方差反应，方差可以通过一个神经网络得到计算，所以最终模型为了更好的重构会尽量让模型的方差为零，而方差为零时，就不存在随机性了，这样模型最终会是一组均值，便退化成了普通的 AutoEncoder。

为了防止噪声为零不再起作用，VAE 会让所有的后验分布都向标准正态分布看齐，衡量两个分布的距离，我们有 KL 散度：

其中，d 为隐变量的维度。

变分自编码中的变分是指变分法，用于对泛函 求极值。

我们将约束两个分布的 KL 散度加入到损失函数中，则有：

简单来说，VAE 的本质就是利用两个编码器分别计算均值和方差，然后利用解码器来重构真实样本，模型结构大致如下：

2.2 VGAE

我们再来看一下变分图自编码，先来看下框架：

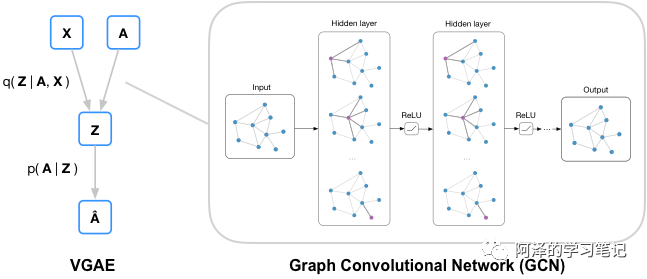
其中，X 为节点的特征矩阵，A 为邻接矩阵，先利用后验概率得到隐变量 Z，再用隐变量重构邻接矩阵 A。

VGAE 的编码器是一个两层的图卷积网络：

其中，后验概率和 VAE 的解决方案一致：

其中， 是特征向量的均值； 是节点向量的方差。

两层卷积神经网络定义为：

其中， 和 共享第一层参数 ，不共享第二层参数 ； 是对称标准化邻接矩阵。

VGAE 的解码器则是利用隐变量的内积来重构邻接矩阵：

其中，.

损失函数也是包括两部分：

其中， 表示

2.3 GAE

除了变分自编码器外，作者也提出了非概率模型的图自编码器（Graph Auto Encoder），公式如下：

其中， 。

此时的损失函数只包括重构损失。

3.Experiment

简单看一下实验部分，主要是边预测问题，我们也可以看到 VGAE 是预测邻接矩阵的。

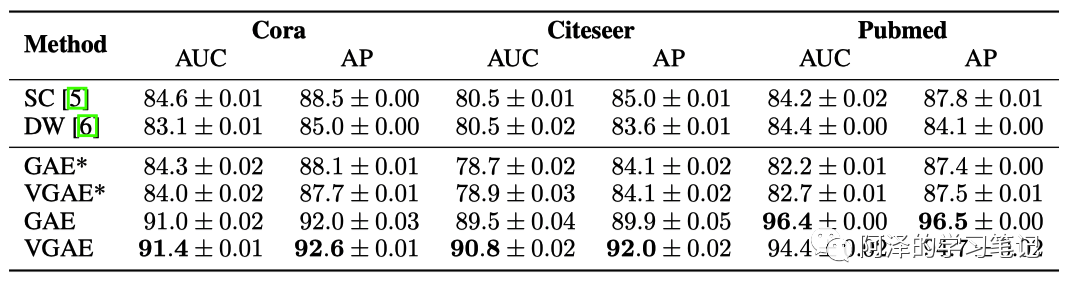
打星号的是不使用节点的特征。

4.Conclusion

总结：VGAE 利用神经网络学习后验分布从而实现编码过程，同时利用重构误差和 KL 散度进行参数优化，从而得到节点的隐变量作为节点的 Embeding。

5.Reference

1. 《Variational Graph Auto-Encoders》
2. 《Auto-Encoding Variational Bayes》
3. 《变分自编码器（一）：原来是这么一回事》

推荐阅读

AINLP年度阅读收藏清单

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

太赞了！Springer面向公众开放电子书籍，附65本数学、编程、机器学习、深度学习、数据挖掘、数据科学等书籍链接及打包下载

数学之美中盛赞的 Michael Collins 教授，他的NLP课程要不要收藏？

自动作诗机&藏头诗生成器：五言、七言、绝句、律诗全了

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

这门斯坦福大学自然语言处理经典入门课，我放到B站了

征稿启示 | 稿费+GPU算力+星球嘉宾一个都不少

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。